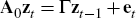RDP 2013-14: Reserves of Natural Resources in a Small Open Economy 5. Robustness

We now consider the robustness of our findings to some of our identifying assumptions.

5.1 Can a VAR Recover the Structural Responses?

As discussed in Section 4.2, a subset of the model parameters are estimated using a GMM procedure that matches the IRFs obtained from our theoretical model with those of the VAR discussed in Section 2. An important question is whether the estimated VAR is consistent with our theoretical model.^[27] To address this question, we simulate data from the general equilibrium SOE model with endogenous reserves, and estimate a VAR on the simulated data using the same specification as that used in Section 2.^[28] We then compare the difference between the model-theoretic IRFs, and those of the VAR estimated on simulated data, to understand whether the VAR is able to identify the model-theoretic effect of a resource price shock.

The comparison between the model-theoretic IRFs for the small open economy with endogenous reserves, and the IRFs obtained from the VAR estimated on simulated data are reported in Figure 6. The relatively small discrepancy between the IRFs confirms that the specification of the VAR in Section 2 can recover the model-theoretic effects of a shock to resource prices asymptotically. This suggests that our identification strategy is locally valid around the parameter vector used in our simulation.

The reason that the VAR specification is able to reproduce the model-theoretic IRFs is the inclusion of reserves, a key observable state variable in our model. If we did not use reserves to deflate both non-resource production and resource capital expenditure, a VAR(1) would not be able to recover the model-theoretic IRFs. Our findings can be interpreted as numerically checking the conditions for identification that are discussed more generally in Ravenna (2007).^[29]

5.2 Imposing Additional Restrictions on the VAR

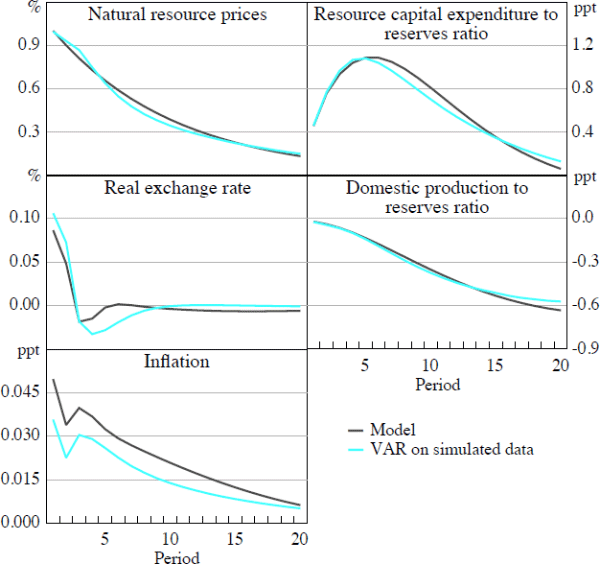
A second identification question relates to the assumption that resource prices are contemporaneously uncorrelated with domestic variables when identifying the IRFs in the VAR, but are assumed to be a statistically independent AR(1) process in the theoretical model. Revisiting the VAR discussed in Section 2,

the VAR only assumes that A₀ has ones along its main diagonal and zeros on the off diagonal elements for the first row. The theoretical model makes the same assumptions, and in addition assumes that the off-diagonal elements of the first row of Γ are also zero, implying that resource prices are an independent AR(1) process. To check whether this is important, we estimate a VAR imposing the additional restrictions on Γ. Specifically, we estimate an AR(1) for resource prices using long-run annual data, from 1900 to 2011 (making use of all available information on resource prices), and then estimate the remaining equations of the VAR using limited information methods on the sample from 1976 to 2011, for which data on annual reserves are available.

Comparing the IRFs for this alternative VAR, with the VAR used in Section 2, the IRFs in response to a resource price shock are qualitatively similar (Figure 7). Although imposing the extra restrictions reduces the amplification of the IRF functions a little, since shocks to resource prices are now estimated to be smaller and less persistent, for the purposes of estimation – that is, matching the theoretical model to either of these VARs – the results are similar and the qualitative implications of our mechanism remain the same.

Footnotes

There has been some debate on the ability of VARs (or more precisely structural VARs) to recover structural shocks. See, for example, the discussion in Christiano, Eichenbaum and Vigfusson (2007) and Chari, Kehoe and McGrattan (2008). [27]

More precisely, we simulate the model for 1,000 periods at the parameter vector identified in Tables 1, 2 and 3 assuming equal standard deviations (at 0.01) for shocks to resource prices, non-mining technology, foreign demand for non-resource exports, the foreign price level, and the price level for investment goods that are uncorrelated. We then estimate a VAR(1) on the simulated data using resource prices, the real exchange rate, the ratio of domestic production to reserves, the ratio of resource investment to reserves and consumer price inflation in that order and including a constant but no deterministic trend. Consistent with Section 2, we assume that resource prices are contemporaneously uncorrelated with the other variables in the system and use this to identify the effects of a resource price shock. [28]

To be clear, asymptotic identification should not be expected a priori. In general, the omission of state variables from the model, for example mining capital which is not directly observed, may imply that a finite VAR representation may not exist for the set of observables used in estimation (for further discussion, see Ravenna (2007)). [29]