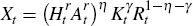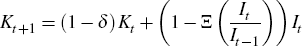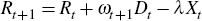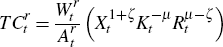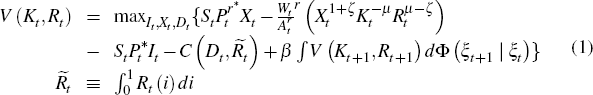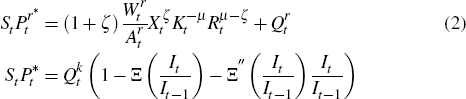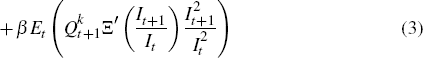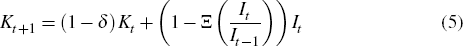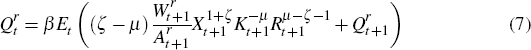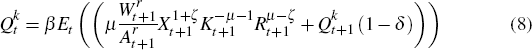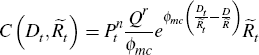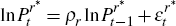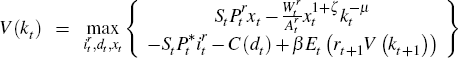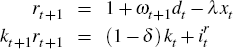RDP 2013-14: Reserves of Natural Resources in a Small Open Economy 3. Natural Resources in Partial Equilibrium
December 2013 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 863KB
3.1 The Resource Sector
Our model of the resource sector draws on the work of Bohn and Deacon (2000). These authors allow for both endogenous exploration and depletion, and use an approach that lends itself to incorporating a resource sector into a small open economy model. For the structure of the resource sector, we assume that:
- All resources are exported at prices that are taken as given by resource firms (that is, the resource market is globally competitive).[7]
- Resource firms can choose to extract a commodity from existing reserves and can engage in costly exploration activity to discover new reserves.
- Resource firms use domestic labour, imported capital, and reserves to extract their natural resource.
- All resource firms are identical in terms of their access to exploration and extraction technologies.
These assumptions are designed to provide an approximation of the resource sector in aggregate. In the Australian context, they are consistent with the fact that the majority of extracted natural resources are exported, that firms engage in both exploration and extraction activity, and that firms import capital and use domestic labour.[8]
Formally, we assume a continuum of identical resource firms of unit measure. Each
period a firm uses capital (Kt), labour 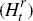 and its existing stock of natural reserves
(Rt), to extract a natural commodity (Xt)
according to a Cobb-Douglas technology:
and its existing stock of natural reserves
(Rt), to extract a natural commodity (Xt)
according to a Cobb-Douglas technology:
where 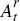 allows for labour-augmenting technical change. There are two additional constraints
for a resource firm. One is the law of motion for resource-specific capital
owned by the firm:
allows for labour-augmenting technical change. There are two additional constraints
for a resource firm. One is the law of motion for resource-specific capital
owned by the firm:
where Kt is resource-specific capital, δ is the rate of depreciation, It is a resource-specific investment goods (purchased from abroad), and Ξ is a real convex investment adjustment cost function. The law of motion for resource-specific capital is standard, although we allow for adjustment costs on changes in investment (rather than the level of investment relative to the capital stock). This is a convenient reduced-form assumption for capturing time-to-build constraints and lumpiness at the level of individual investment projects. Modelling adjustment costs in this way captures the typical ‘hump-shaped’ response of resource-specific investment to resource price shocks (as shown in Figure 2).
The second constraint is the law of motion for reserves:
where reserves are depleted through production (extraction) Xt and accumulated through Dt, a measure of exploration (or discovery) activity. The parameter λ is an indicator variable that is one in a model with depletion and zero in a model without depletion. This is useful for defining the equilibria with and without endogenous reserves discussed further below.
We assume that exploration activity is an uncertain process, captured by the random variable ωt+1, which only becomes known at the beginning of period t + 1. We assume ωt+1 is independently and identically distributed on a compact support with distribution function Γ and first moment E (ωt+1) = 1. This implies that the probability that a unit of exploration results in the successful discovery of a unit of new reserves is independent of the state of the economy.
Given the assumption of Cobb-Douglas production technology, the total wage bill for
a resource firm, 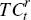 ,
is given by:
,
is given by:
where 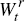 is the wage paid to labour and, following Bohn and Deacon (2000), we define the
parameters
is the wage paid to labour and, following Bohn and Deacon (2000), we define the
parameters 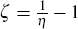 and
and 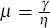 .
The firm chooses its investment in resource-specific capital, its extraction,
and exploration expenditure by solving the following dynamic program:
.
The firm chooses its investment in resource-specific capital, its extraction,
and exploration expenditure by solving the following dynamic program:
where Kt+1 and Rt+1 are
given by the constraints previously described; V : R2→R
is the value function; St is the nominal exchange rate
(measured in units of domestic currency required to purchase a single unit
of foreign currency); 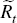 is the aggregate stock of domestic reserves;
is the aggregate stock of domestic reserves;
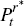 is the price of the extracted commodity in foreign currency terms;
is the price of the extracted commodity in foreign currency terms; 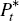 is the price of investment
goods (imported from abroad) that deliver resource sector-specific capital
in the next period (also measured in foreign currency prices); β
is a discount
factor,[9]
ξt is a state vector containing exogenous prices and
aggregate reserves which are known at time
is the price of investment
goods (imported from abroad) that deliver resource sector-specific capital
in the next period (also measured in foreign currency prices); β
is a discount
factor,[9]
ξt is a state vector containing exogenous prices and
aggregate reserves which are known at time 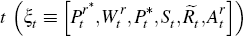 ; and C : R2→R
is a convex cost function associated with exploration activity. The precise
functional form and parametrisation of the cost function are discussed below.
; and C : R2→R
is a convex cost function associated with exploration activity. The precise
functional form and parametrisation of the cost function are discussed below.
Uncertainty over future prices, the aggregate stock of reserves, and the success
of future exploration are captured in the expectation of the value function
in the next
period.[10]
In the partial equilibrium analysis that follows, we assume that the factor
prices and the real exchange rate 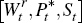 remain constant in
the face of a resource price shock.
remain constant in
the face of a resource price shock.
Our approach is quite similar to that adopted in Bohn and Deacon (2000). However, one important difference is that we abstract from the presence of a known finite bound on the cumulative level of resources to be discovered. Consistent with Pindyck (1978), we assume that additional reserves can be discovered in perpetuity but that it is costly to discover new reserves as the stock of known reserves increases. This assumption is important for our analysis because it implies that the policy functions that solve the resource firms' problem in Equation (1) are time invariant, and so can be integrated with a DSGE model. As well as increasing tractability, we think that this assumption is realistic for many countries, including Australia, given that reserves, production and exploration have continued to grow over time rather than decrease as one would expect in a model of fixed potential reserves.[11]
The first-order conditions associated with the resource firms' problem are given by:
The marginal valuations of an extra unit of reserves and capital to the firm are respectively given by:
Equation (2) implies that firms equate the marginal revenue of extraction with the marginal cost of extraction, where the marginal cost of extraction includes both the additional cost of extraction in period t, and the opportunity cost tied to the fact that resources extracted today cannot be extracted in future periods. Equation (3) implies that the marginal cost of purchasing resource-specific capital from abroad is equal to the marginal return of this capital after accounting for the fact that additional investment reduces future investment-adjustment costs.
Equation (4) implies that firms equate the marginal cost of exploration with the expected marginal return, the latter being given by the shadow price of an extra unit of reserves. Equations (5) and (6) describe the law of motion for capital and the stock of natural reserves, respectively. The shadow prices in Equations (7) and (8) reflect the marginal valuations of an additional unit of reserves and an additional unit of capital respectively, and are given by the present discounted value of the additional revenue streams generated by either an extra unit of reserves or capital.
We compare two equilibria associated with these first-order conditions. The first assumes that resources are depletable (λ = 1) and exploration expenditure responds to changes in prices.
Definition 1. A partial equilibrium for the endogenous reserves model is given by sequences for
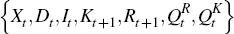 that solve Equations (2) to (8) taking the expected sequences
that solve Equations (2) to (8) taking the expected sequences 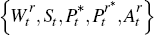 as given and assuming λ
= 1.
as given and assuming λ
= 1.
The second equilibrium we consider assumes that the stock of resources is exogenous (fixed), and thus abstracts from both depletion and the scope for exploration activity.[12]
Definition 2. A partial equilibrium with exogenous reserves, is given by sequences
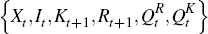 that solve Equations (2) to (3) and (5) to (8) taking the expected sequences
that solve Equations (2) to (3) and (5) to (8) taking the expected sequences
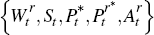 as given and assuming λ = 0 and Dt = 0 for all t.
as given and assuming λ = 0 and Dt = 0 for all t.
3.2 Calibration
Table 1 reports the calibration of the structural parameters with the model solved at an annual frequency – the highest frequency for which production and reserves data are available. The discount factor and depreciation rate are chosen to be in line with existing literature that model a resource sector.[13] The exponents on capital and labour in the resource extraction technology (γ and η) are chosen to match a steady state rate of annual extraction of two per cent, and a wage bill relative to total revenue of approximately 11 per cent.[14] The two per cent average annual extraction rate is consistent with an equally-weighted average of extraction rates in iron ore, coal, gold, lead, nickel, zinc, copper and bauxite for the sample 1976 to 2011.[15]
| Description | Coefficient | Value |
|---|---|---|
| Calibrated parameters | ||
| Discount factor | β | 0.96 |
| Labour factor exponent | η | 0.13 |
| Capital factor exponent | γ | 0.49 |
| Depreciation rate | δ | 0.10 |
| Parameters obtained from GMM estimation of general equilibrium model | ||
| Exploration costs dynamics | ϕmc | 0.5 |
| Investment cost parameter | κ | 3 |
| AR(1) parameter (prices) | ρr | 0.9 |
For the parameterisation of exploration costs, we use a function that implies that resource sector profits are homogenous of degree one:[16]
where ϕmc is a parameter that governs the sensitivity of
exploration costs to shocks and, thus, the incentive to engage in exploration
activity; Qr is a normalisation used to ensure a well-defined
steady state (in general equilibrium); and 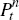 is the price of a bundle
of non-traded goods (held fixed for the partial equilibrium analysis).
is the price of a bundle
of non-traded goods (held fixed for the partial equilibrium analysis).
Importantly, and as discussed further in Appendix B, this cost function satisfies
the restrictions that: exploration costs are increasing in both exploration
and aggregate reserves, 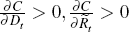 ; the derivative of the marginal cost of exploration
is increasing in the level of exploration,
; the derivative of the marginal cost of exploration
is increasing in the level of exploration, 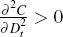 ; and that this latter
derivative is sufficiently large to outweigh any reduction in the marginal
costs of exploration that are tied to larger existing reserves permitting extensions
of, or new finds linked to, existing deposits,
; and that this latter
derivative is sufficiently large to outweigh any reduction in the marginal
costs of exploration that are tied to larger existing reserves permitting extensions
of, or new finds linked to, existing deposits, 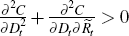 .
.
For the parameteristation of investment adjustment costs, we assume a quadratic adjustment cost function satisfying Ξ′(1) = 0,Ξ″(1) = κ. For resource prices, we assume that the natural log of prices follows an AR(1) process with autoregressive parameter ρr:
where 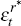 is iid. All other prices
is iid. All other prices 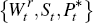 are held fixed in partial equilibrium.
are held fixed in partial equilibrium.
The parameters ϕmc, κ and ρr only affect the shape of IRFs and have no bearing on the steady state of the model. For this reason, the values for these parameters are chosen to be consistent with the values implied when matching the IRFs of the general equilibrium version of our model (discussed further below) with the VAR discussed in Section 2.
3.3 Results
Figure 3 highlights the IRFs associated with a 1 per cent positive shock to resource prices in partial equilibrium – that is, holding wages, the exchange rate and the price of imported capital fixed. The IRFs are computed under both the endogenous and exogenous reserves equilibria as described in Definitions (1) and (2). Comparing these two equilibria, it is clear that the endogenous model generates additional amplification and persistence in response to a resource price shock. Factor utilisation for both labour and capital increase by more in the endogenous reserve model, as does the level of extraction. The stock of reserves also increases in the endogenous reserve model (but is held constant by assumption with exogenous reserves) as exploration activity and the discovery of new deposits results in reserves accumulating faster than they are depleted through higher extraction.
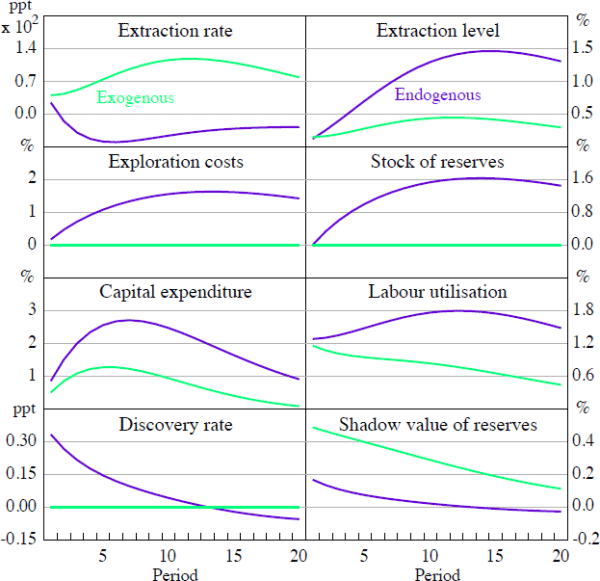
The mechanism driving the amplification of the resource price shock is the feedback effects that occur through exploration. Because a persistently higher resource price provides firms with an incentive to engage in the exploration of new reserves, or to find extensions to existing deposits, the expected value of newly discovered reserves increases. This leads firms to engage in exploration activity. Importantly, any newly discovered reserves are a permanent addition to the resource firms' extraction opportunity set. That is, once discovered, they can be extracted either in the next period or in any future period without depreciation.
Under the assumption of Cobb-Douglas technology, reserves are complementary to both labour and capital; and so as more reserves are discovered, the marginal product of labour and capital both increase. Resource firms' respond by investing in additional capital and hiring more labour, leading to a greater expansion in all areas of mining operations.
An interesting implication of this partial equilibrium model is that reserves will have non-stationary dynamics in equilibrium. That is, transitory changes in resource prices can generate permanent changes in investment, labour utilisation, resource sector production and the stock of reserves. To see why, note that if we abstract from investment adjustment costs, the problem for a resource producer can be reformulated as:
subject to:
In this representation, the decision variables are reformulated in terms of the extraction
rate, 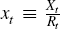 ,
the exploration (discovery) rate,
,
the exploration (discovery) rate, 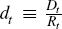 , and the investment
rate,
, and the investment
rate, 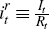 ;
and (rt+1−1) is now the growth rate in
reserves.[17]
;
and (rt+1−1) is now the growth rate in
reserves.[17]
This reformulation makes it clear that one can think of a resource producer as choosing
its optimal extraction rate, exploration rate, and investment rate. As discussed
in further detail in Appendix C, the solution to these decision
variables are a function of underlying prices and technology, 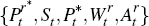 but not the stock of
reserves. This in turn implies that a resource firms' scale of operation
is directly proportional to the stock of reserves and that any newly discovered
reserves will imply permanent changes in the levels of extraction, exploration
and investment, but only transitory changes in the optimal extraction, exploration
and investment rates. This result helps to explain the degree of amplification
and persistence in the IRFs, and implies that the scale of the resource sector
can appear to trend over time, even if real resource prices exhibit long-run
mean reversion (stationarity) as we have assumed.
but not the stock of
reserves. This in turn implies that a resource firms' scale of operation
is directly proportional to the stock of reserves and that any newly discovered
reserves will imply permanent changes in the levels of extraction, exploration
and investment, but only transitory changes in the optimal extraction, exploration
and investment rates. This result helps to explain the degree of amplification
and persistence in the IRFs, and implies that the scale of the resource sector
can appear to trend over time, even if real resource prices exhibit long-run
mean reversion (stationarity) as we have assumed.
In view of the additional amplification generated in response to a resource price shock, we now investigate whether the same results hold in general equilibrium, and whether the incorporation of endogenous reserves alters the effects of a resource price shock on the rest of the economy.
Footnotes
For simplicity, we abstract from the use of commodities in domestic production. It should also be noted that perfect competition is the norm in literature modelling a resource sector within a small open economy. [7]
See Connolly and Orsmond (2011) for further discussion. [8]
In partial equilibrium we abstract from a stochastic discount factor since firm ownership is not modelled explicitly. We allow for a stochastic discount factor in the general equilibrium model in Section 4.1. [9]
Note since ωt+1 is iid with a unitary first moment, we can integrate this variable out of the term Et (V (Kt+1,Rt+1)). [10]
See Appendix B for further discussion and Pindyck (1978). [11]
It is straightforward to verify that the steady states for these equilibria exist and are identical. [12]
See, for example, Charnavoki (2010) and Garcia and González (2010). [13]
This estimate is consistent with estimates from Topp et al (2008) and ABS Catalogue No 8414.0. [14]
More specifically, we use an arithmetic average across these industries using both the extraction weights implied when using economically demonstrated reserves (2.8 per cent per annum) and total reserves (1.65 per cent per annum), where the latter also include sub- and para-marginal reserves. [15]
That is, a doubling of production and of all factor inputs, including reserves, would double revenue and double cost. [16]
Note that we have made use of the fact that when the constraints and return functions are both homogenous of degree one, the value function is also homogenous of degree one. For further discussion, see Appendix C. [17]