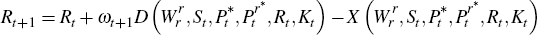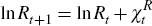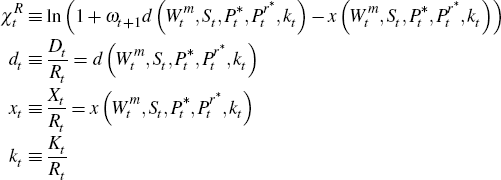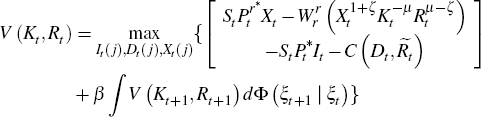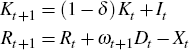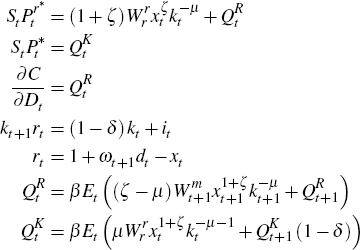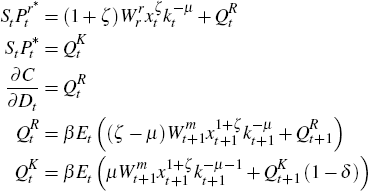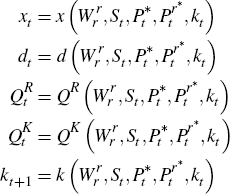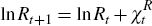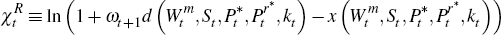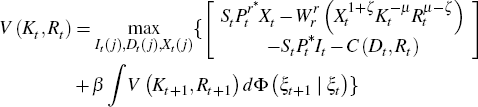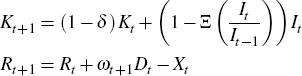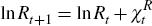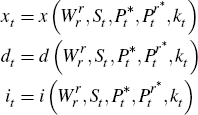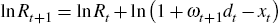RDP 2013-14: Reserves of Natural Resources in a Small Open Economy Appendix C: Analysis of the Partial Equilibrium Model

Proposition 1. In the absence of investment adjustment costs, the equilibrium law of motion for reserves

can be rewritten as

where

Proof. In the absence of investment adjustment costs the firms' decision problem is given by

subject to:

The associated first-order conditions at an interior solution are

Note that the solutions to can be solved from the simplified system

yielding the policy functions

Noting that these policy functions do not include R_t in their argument, it follows that the law of motion for log reserves in equilibrium will be given by

where

is not a function of reserves, and so log reserves will have a unit root in equilibrium.

Proposition 2. Assume the firm solves the following dynamic program

subject to:

and where C(D_t,R_t) is homogeonous of degree one. In this case the equlibrium law of motion for log reserves can be also written as

where 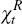is defined in Proposition 1.

Proof. This proof follows noting that the profit function is homogenous of degree one when C(D_t,R_t) is homogeonous of degree one. Since the constraints are also linearly homogeonous, the value function itself is linear homogenous and the associated policy functions are homogenous of degree one in the state variables K_t and R_t (see Stokey and Lucas (1989, Section 9.3) for a formal treatment). This implies the policy functions can be written as

and so the log-level of reserves in equilibrium will be given by

where d_t and x_t are not direct functions of R_t in the solution to the above program.