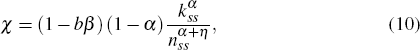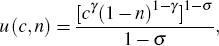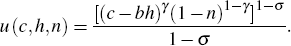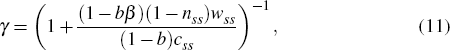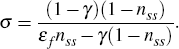RDP 2013-08: International Business Cycles with Complete Markets 3. Parameter Values and Computation
June 2013 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 736KB
We solve the benchmark model numerically using the parameter values reported in Table 1. Some of these values are common to the international business cycle literature. The capital income share α, utility curvature σ, and parameters governing the stochastic process for productivity take the values found in Kehoe and Perri (2002). The Frisch elasticity of labour supply 1/η is set to 1.43, as in Correia et al (1995) who incorporate GHH preferences in a small open economy setting. Since we introduce habits to account for investment behavior, we use an estimate from the asset pricing literature. By setting the habit intensity parameter b to 0.73, we follow Jermann (1998), who considers a closed-economy counterpart to our model with inelastic labour supply.[3]
| Benchmark model | |
|---|---|
| Preferences | β = 0.989, σ = 2, b = 0.73, η = 1/1.43, χ = 1.401 |
| Technology | α = 0.36, δ = 0.025 |
| Productivity shocks | ρ = 0.95, ν = 0, σε = 0.007, ρε = 0.25 |
| Variations | |
| BKK productivity process | ρ = 0.906, ν = 0.088, σε = 0.00852, ρε = 0.258 |
| High Frisch elasticity | 1/η = 1.8 |
| Low Frisch elasticity | 1/η = 1 |
| GHH preferences | b = 0, χ = 5.0388 |
| Standard preferences | b = 0, σ = 1.8254, 1 − γ = 0.6303 |
| Standard preferences/habits | σ = 1.8095, 1 − γ = 0.6369 |
| Notes: One period of time corresponds to one quarter. The adjustment cost parameter, ξ, is set to fit the standard deviation of investment relative to the standard deviation of output in the data. The preference parameter χ (1−γ under standard preferences) that controls disutility from providing labour is set to ensure that hours worked in the steady state equal 1/3. Other parameters in the variations are the same as in the benchmark model. | |
Other parameters are calibrated to match long-run averages in the US data as described in Cooley (1997). One period of time corresponds to one quarter. The quarterly depreciation rate δ is set to ensure that the steady-state investment-output ratio is 0.25 and the capital-output ratio is 10. Once δ is set, the discount factor β follows directly from the Euler equation (Equation (9)) in the steady state.[4] The coefficient that controls disutility from providing labour, χ, is set so that the agents spend 1/3 of their unit time endowment on market activities in the deterministic steady state, nss. Its value follows from Equation (8) in the deterministic steady state:
where 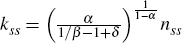 ,
is the steady-state level of the capital stock.
,
is the steady-state level of the capital stock.
In the variations we consider Cobb-Douglas preferences (also referred to as ‘standard’ preferences)
and their time non-separable version
The weight of leisure in the instantaneous utility function, 1 − γ, ensures that the steady-state level of hours worked nss remains at 1/3. The weight depends on the intensity of habits
where wss = (1 − α)(kss/nss)α is the steady-state real wage. As in Raffo (2008), we keep the Frisch elasticity of labour supply εf constant across the models. To accomplish this we adjust the curvature parameter σ to account for variation in γ across models with different levels of habit intensity:
The curvature parameter σ takes the value 1.8095 for b = 0.73 and 1.8254 for the time separable case (b = 0). In all simulations, the capital adjustment cost parameter ξ is set to match the observation that the standard deviation of investment is 2.88 times higher than that of output.
We solve the model numerically using an Euler equation-based method that does not require linearisation of the optimality conditions. The algorithm replaces conditional expectations in the first order conditions with smooth parametric functions of the current state variables and iterates on the parameter values until the rational expectations equilibrium is achieved (den Haan and Marcet 1990). The details of implementation are described in Appendix B.
Footnotes
Values for habit intensity within the range of 0.69 to 0.9 have been reported to help explain the equity premium puzzle (Constantinides 1990; Jermann 1998; Boldrin et al 2001). In the sensitivity analysis, we report results from simulations of the model for the whole range of the habit parameter b ϵ [0,1). [3]
Given the values of α, δ and the steady-state capital-output ratio kss/yss, we compute the discount factor as β = (α (yss/kss) + 1 − δ)−1. [4]