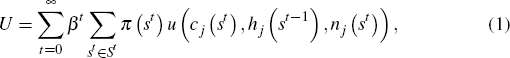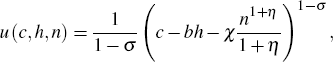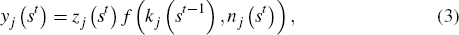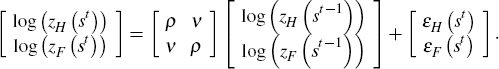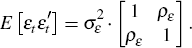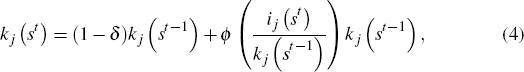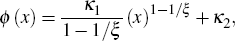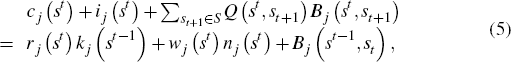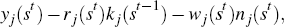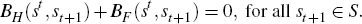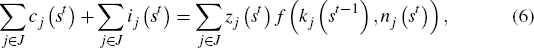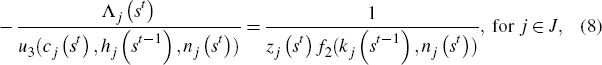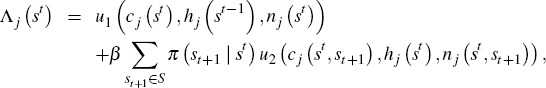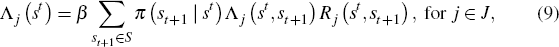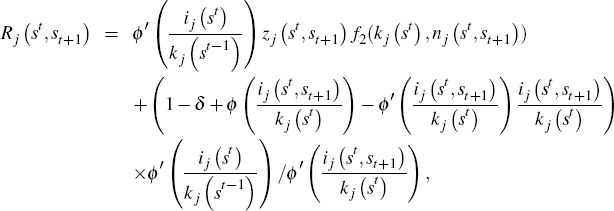RDP 2013-08: International Business Cycles with Complete Markets 2. The Model

The general structure of the model is similar to Backus et al (1992) (henceforth BKK).

2.1 The Economies

The world consists of two countries. The same parameters describe technology and preferences in both countries. Each country j ϵ J = {H,F} is populated by a continuum of identical infinitely lived individuals. The two countries produce a single good that can be either consumed or invested. Labour is immobile across countries. In each period t, the world economy experiences an event s_t drawn from the countable set of events, S. Let s^t = (s₀, s₁, …, s_t) ϵ S^t denote the history of events from time 0 to time t. The time-0 probability of any given history s^t is denoted by π(s^t).

Consumers Habit-forming agents have their preferences defined over stochastic sequences of consumption, habits, and leisure

where β ϵ (0,1) is the discount factor, c_j(s^t) denotes household consumption at time t in country j after realisation of history s^t, and n_j(s^t) ϵ [0,1] denotes individual labour supply. Time endowment per period is normalised to one. The stock of habits h_j(s^t−1) with which the agent enters period t equals her own consumption in period t − 1:

The instantaneous utility function takes the following form:

where σ is the curvature parameter, χ determines relative importance of leisure, 1−n, and habit adjusted consumption, c−bh. The parameter b ϵ [0,1) denotes the intensity of habit formation and introduces time non-separability of preferences. The Frisch elasticity of labour supply is given by 1/η.

This specification of preferences has been used by Monacelli and Perotti (2008) to explore the transmission of government spending shocks, and by Boileau and Normandin (2005) to study current account fluctuations in a small open economy model. It nests two well-known special cases. As η tends to infinity, the labour supply becomes inelastic and the preference structure reduces to the internal linear habit formation preferences popularised by Constantinides (1990). When b = 0 the model features regular GHH preferences.

Producers The households supply labour and capital to firms, which have access to constant returns-to-scale technology. Production is subject to a country-specific exogenous random shock, z_j (s^t), to total factor productivity (TFP). Output in country j after history s^t is given by

where k_j (s^t−1) denotes the capital stock used at time t by the firms in country j. The production function is Cobb-Douglas: f(k,n) = k^αn^1−α. The TFP shocks follow a stationary vector autoregressive process (VAR) in logs:

Diagonal elements of the transition matrix, ρ, determine the degree of persistence in productivity within each country. When off-diagonal elements, ν, are different from zero, productivity innovations originating in one country spill over national borders. The innovations to the productivity process are zero mean serially independent bivariate normal random variables with the contemporaneous covariance matrix

The capital stock in each economy evolves over time according to the following law of motion:

where δ is the depreciation rate of capital. An adjustment cost function ϕ satisfies ϕ (·) > 0, ϕ′ (·) > 0, and ϕ″ (·) < 0. This formulation has been used by Baxter and Crucini (1995), Baxter and Farr (2005) and Yakhin (2007) in the context of international business cycle models. Since we do not rely on log-linearisation methods for solving the model, we must specify the functional form for capital adjustment costs explicitly. We adopt the following formulation from Boldrin, Christiano and Fisher (2001)

where 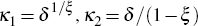, and ξ, is the elasticity of investment with respect to Tobin's q. The restrictions ϕ (δ) = δ and ϕ′ (δ) = 1 imposed on the constants κ₁ and κ₂ ensure that incorporation of the adjustment cost does not affect the deterministic steady state of the model.

Asset markets Agents have access to a complete set of state-contingent claims. A claim that sells internationally for Q (s^t,s_t+1) at time t, after realisation of history s^t, entitles the bearer to a unit of the consumption good in the following period provided that the state s_t+1 is realised. Denoting by B_j (s^t,s_t+1) the quantity of such claims purchased by the residents of country j, their budget constraint can be written as

where w_j (s^t) is the wage and r_j (s^t) is the rental rate on capital in country j.

Equilibrium The equilibrium in this environment consists of the state-contingent sequences of prices 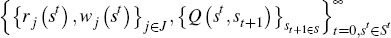and allocations 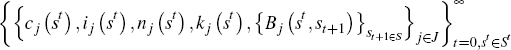that satisfy the following conditions:

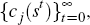
1. Given prices, consumers choose state-contingent sequences 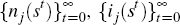and bond holdings 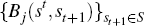for all s^t ϵ S^t, to maximise utility subject to the budget constraint and the initial conditions.

2. Given prices, firms choose n_j(s^t) and k_j(s^t−1) to maximise profits

   

   View MathML

   subject to technology and the non-negativity constraints n_j(s^t) ≥ 0 and k_j(s^t−1) ≥ 0.

3. Asset market clearing requires that for all t ≥ 0 and for all s^t ϵ S^t,

   

   View MathML

Optimality conditions An equilibrium allocation in this economy can be computed as the solution to a social planner's problem. In addition to the equations of motion, Equations (2) and (4), the global resource constraint

and the initial conditions and the transversality conditions, the optimal allocations must satisfy the following first order conditions. First, under complete markets, the marginal utilities of consumption of two agents are equalised for each time and state

Second, labour supply is controlled by the intratemporal condition

where u₃ (·) denotes the partial derivative of the utility function with respect to its third argument and f₂ (·) denotes the partial derivative of the production function with respect to its second argument. The marginal utility of consumption of agent j after history s^t is

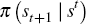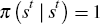where denotes the conditional probability of s_t+1 given s^t, and . Third, intertemporal choice is governed by the Euler equation given by

where

is the one-period gross rate of return on capital installed in country j after realisation of history (s^t,s_t+1).