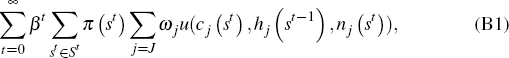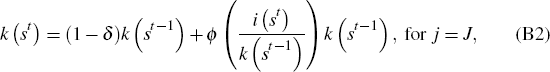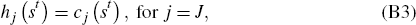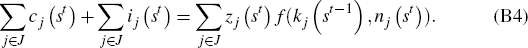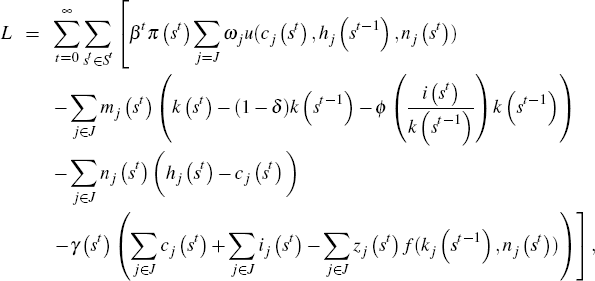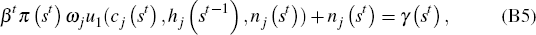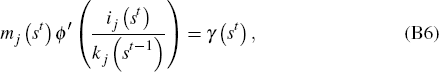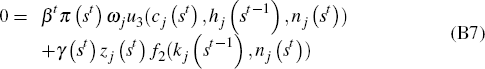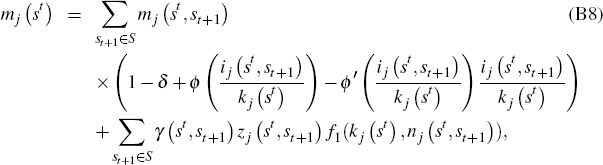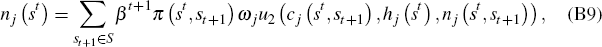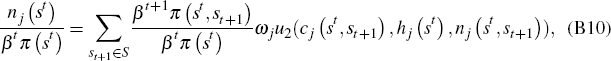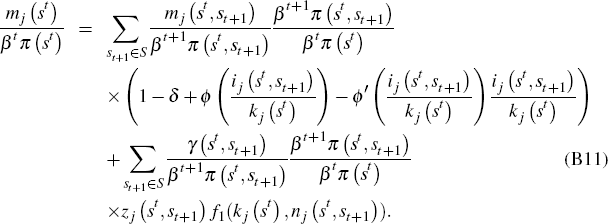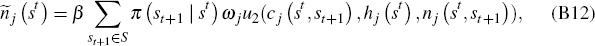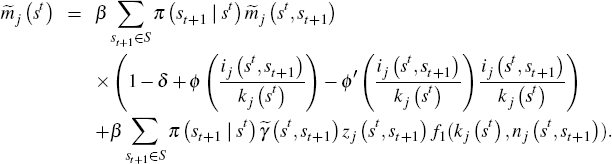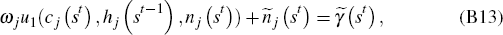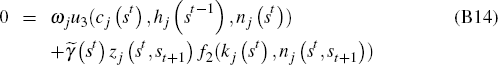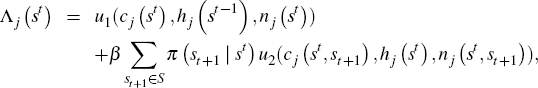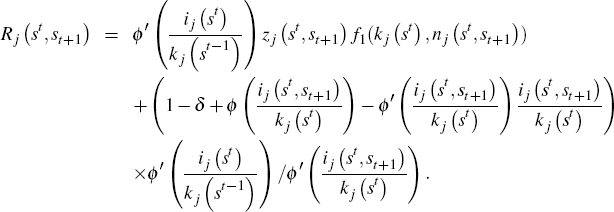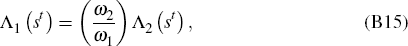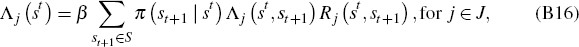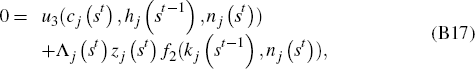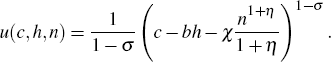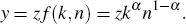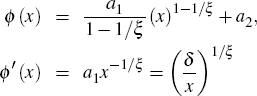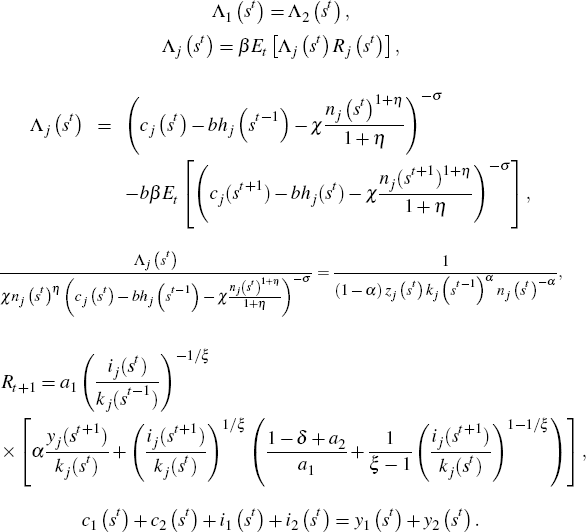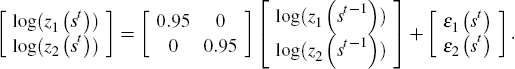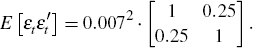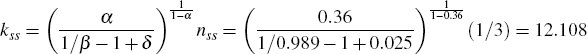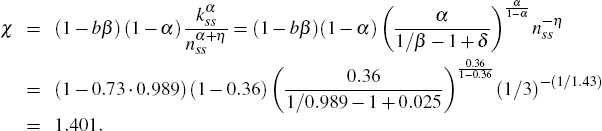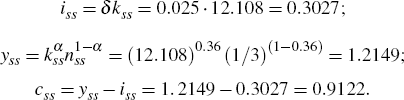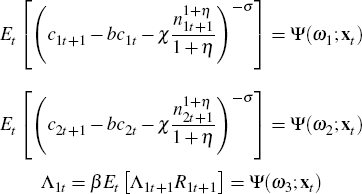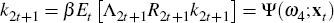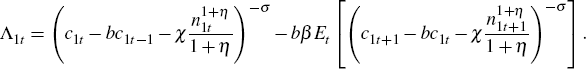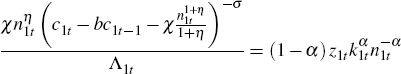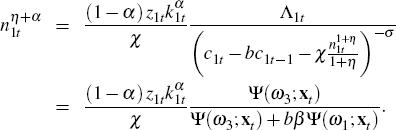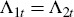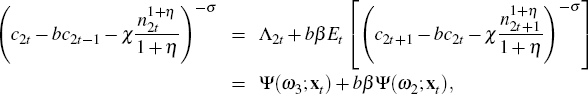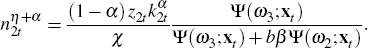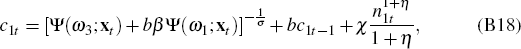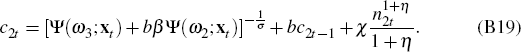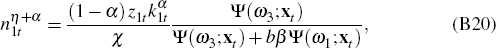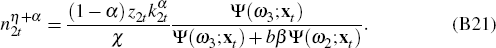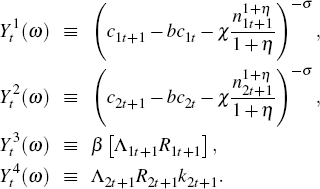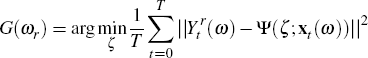RDP 2013-08: International Business Cycles with Complete Markets Appendix B: Solving the Model
June 2013 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 736KB
B.1 The Optimality Conditions
An equilibrium allocation in this economy can be computed as the solution to a social
planner's problem. Taking the initial conditions 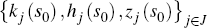 as given, the planner chooses state-contingent plans
as given, the planner chooses state-contingent plans 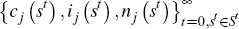 for each agent j
ϵ J = {1,2} to maximise the expected discounted sum of their
weighted utilities
for each agent j
ϵ J = {1,2} to maximise the expected discounted sum of their
weighted utilities
subject to the law of motion for capital
the law of motion for habits
as well as the global resource constraint
The Lagrangian associated with the planner's problem is given by
where 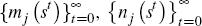 and
and 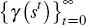 are the state-contingent paths of Lagrange multipliers associated with constraints
in Equations (B2), (B3), and (B4). Equating the gradient of the Lagrangian
to zero we obtain
are the state-contingent paths of Lagrange multipliers associated with constraints
in Equations (B2), (B3), and (B4). Equating the gradient of the Lagrangian
to zero we obtain
where u1 (·) is the partial derivative of u with respect to its first argument. We use the same notation to denote the other partial derivatives.
The intertemporal conditions given by Equations (B8) and (B9) can be rearranged as
and
By denoting 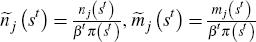 ,
and
,
and 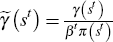 we can rewrite
Equations (B10) and (B11) as
we can rewrite
Equations (B10) and (B11) as
and
In a similar way, Equations (B5) and (B7) can be rewritten as
and
Let Λj (st) denote the marginal utility of consumption of agent j after history st. Then from Equations (B12) and (B13) it follows that
where π (st+1 | st) denotes the conditional probability of st+1 given st, and π (st | st) = 1.
Let Rj (st,st+1) denote the realised one-period gross rate of return on capital in country j after realisation of history (st,st+1)
Then the first order conditions can be reformulated as
for j ϵ J.
B.2 Optimality Conditions with the Functional Forms
The instantaneous utility function takes the form
The production function is
The capital adjustment cost function is
where the restrictions that ϕ′ (δ) = 1 and ϕ (δ)
= δ require that a1 = δ1/ξ
and 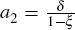 .
Symmetry between the two economies implies that ω1
= ω2. Incorporating specific functional forms, the
optimality conditions can be rewritten as
.
Symmetry between the two economies implies that ω1
= ω2. Incorporating specific functional forms, the
optimality conditions can be rewritten as
B.3 Parameter Values for the Benchmark Model
Productivity follows a process similar to that specified by Kehoe and Perri (2002):
The innovations to the productivity process are zero mean serially independent bivariate normal random variables with the contemporaneous covariance matrix
Standard/estimated values are as follows:
- Capital income share α = 0.36 and coefficient of relative risk aversion σ = 2, as in Kehoe and Perri (2002)
- Elasticity of labour supply 1/η = 1.43, that is, η = 1/1.43 = 0.6993, as in Correia et al (1995)
- Intensity of habits b = 0.73, as in Jermann (1998).
The calibration targets are: nss = 1/3;iss/yss = 0.25;kss/yss = 10. The calibrated parameters are as follows:
- Depreciation rate: δ = iss/kss = (iss/yss)/(kss/yss) = 0.025
- Discount factor: β = (α (yss/kss)+1−δ)−1 = (0.36−0.1+1−0.025)−1 = 0.989
-
From
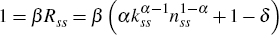 it follows that
it follows that
-
From the labour supply equation in the non-stochastic steady state
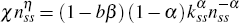 ,
it follows that the weight of labour in the utility function χ
is:
,
it follows that the weight of labour in the utility function χ
is:
The other steady-state values are as follows:
B.4 The Numerical Procedure
The model is solved using a variant of the ergodic set methods described by Maliar, Maliar and Judd (2011). The algorithm we use is classified by Judd, Maliar and Maliar (2009) as belonging to the stochastic simulation class of methods. The approach is to replace conditional expectations with smooth parametric approximation functions of the current state variables and a vector of parameters, and then iterate on the parameter values until a rational expectations equilibrium is achieved. The four conditional expectations are parameterised as follows
where xt = [k1t,k2t,c1t−1,c2t−1,z1t,z2t]. From the first order condition for consumption in the home country we have
Re-arranging yields
From the first order condition for labour in the country 1
it follows that
From the risk-sharing condition:
we obtain
and from the country 2 supply equation we get
Current consumption in each country is therefore given by:
Labour in each country is given by
The algorithm is implemented as follows:[6]
-
Obtain an initial guess for ω = [ω1,ω2,ω3,ω4].
We obtain the initial guess using the genetic algorithm and then homotopy.
Fix kj0 = kss, hj0
= css and zj0 = 1 for j
ϵ J, and draw a sample of size T of the exogenous
stochastic shock
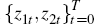 .
.
-
Replace the conditional expectations with the parameterised functions Ψ(ωr;xt),
r = 1…4. Calculate
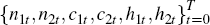 using Equations (B18),
(B19), (B20) and (B21), and the law of motion for habits, Equation (B3). Calculate
using Equations (B18),
(B19), (B20) and (B21), and the law of motion for habits, Equation (B3). Calculate
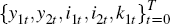 using the production function, the law of motion for capital given in Equation (B2)
and the global resource constraint, Equation (B4). Similarly compute
using the production function, the law of motion for capital given in Equation (B2)
and the global resource constraint, Equation (B4). Similarly compute 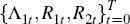 .
.
-
Set
and minimise the sum of squared residuals for the equation
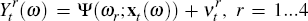 where
where 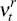 is the regression error. That is, find
is the regression error. That is, find
where ζ, is the parameter vector to be estimated.
-
Iterating on wr, find the fixed point
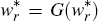 . Update wr
using the algorithm
. Update wr
using the algorithm 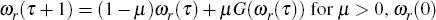 given.
given.
Footnote
Further details on this class of algorithm are provided by den Haan and Marcet (1990). For a more formal description and related proofs, see Marcet and Marshall (1994). [6]