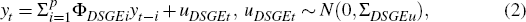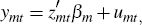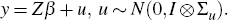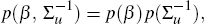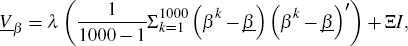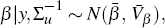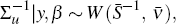RDP 2013-06: Estimating and Identifying Empirical BVAR-DSGE Models for Small Open Economies 2. Methodology – Estimation

The approach taken to estimate the empirical BVAR-DSGE model has several steps:

1. estimating the DSGE model using Bayesian methods
2. using the posterior of this DSGE model to construct a VAR approximation to the DSGE model by simulation methods
3. constructing a prior for the empirical reduced-form BVAR from the VAR approximation to the DSGE, and finally
4. estimating the posterior of the empirical BVAR model.

Each of these steps will be discussed in turn. Before doing so, I introduce some notation.

The reduced-form BVAR to be estimated is of the form:

where 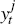are vectors of variables and the superscript L or S denotes the large or small economy. Let 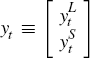, and there be n variables in total. 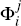are matrices of parameters for lags i = 1 …p; j = SL denotes parameters that are the response of the small economy variables to the large economy variables. Let 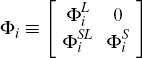. Note that Φ_i has a block of zeros in the upper right so that the large economy does not depend on lags of the small economy variables, which is known as block exogeneity. 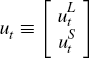are the reduced-form shocks, which are assumed to be normally distributed with a variance-covariance matrix .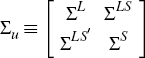

2.1 Estimating the DSGE Model

The DSGE model is estimated using Bayesian methods, as is often done in the literature. The advantage of this is that it allows subjective information about the parameters to be utilised in estimation and, more pragmatically, it may lessen identification issues for some parameters. Bayesian estimation of DSGE models is summarised in An and Schorfheide (2007), and can be implemented, for example, using the pre-processor Dynare in Matlab. The observed variables used to estimate the DSGE model are the same as those included in the reduced-form BVAR.

2.2 Estimating a VAR Approximation to the DSGE Model

The solution to a DSGE model is a VAR in its variables. The structure of the DSGE model places restrictions on the parameters of the VAR. However, only a subset of the variables in the DSGE model are observed, that is, matched to actual data in estimation. The solution in these observed variables alone may be a vector-autoregressive moving average (VARMA) model rather than a VAR. This typically occurs when there is a stock variable (such as capital or net foreign assets) in the model that is not used in estimation. The VARMA model can be approximated with a low-order VAR, although the approximation is likely to become better the higher the order of the VAR. Naturally if the solution to the DSGE model has a VAR representation that can be solved for analytically, that could be used.^[2]

To construct the approximation, for a particular set of DSGE parameters I solve the model, simulate long time series of the observed variables from it, and estimate the following VAR on these simulated data:

where Φ_DSGEi are the matrices of parameters, with block exogeneity imposed, and u_DSGEt are the reduced-form shocks.^[3]

2.3 Constructing a Prior for the Empirical BVAR-DSGE Model

There are two aspects to constructing a prior for the empirical BVAR-DSGE model from this VAR approximation. First, selecting prior distributions which will accommodate block exogeneity, and second, selecting the arguments for the prior.

2.3.1 Selecting the prior distributions

In the approach of Del Negro and Schorfheide (2004), the prior for the BVAR is formed by expressing the likelihood of data simulated from the DSGE model (for a given vector of parameters) in Normal-inverted Wishart form. This means that the prior of the variance-covariance matrix of the reduced-form shocks, given the DSGE parameters, is an inverted Wishart distribution, and the prior for the VAR parameters, conditional on the variance-covariance matrix of the shocks and the DSGE parameters, is Normal. This prior is convenient as it conjugates with normally distributed data, which means that the posterior has a known form. A disadvantage of this prior, however, is that it assumes that the same explanatory variables are in each equation; for a further discussion of this see Koop and Korobilis (2010).

One alternative, which does not make this assumption, is the independent Normal-Wishart prior (Koop and Korobilis 2010). This prior is similar to the Normal-inverted Wishart, except that the prior for the VAR parameters is normally distributed without being conditioned on the variance-covariance matrix of the shocks. This prior allows complete flexibility about whether variables are included or excluded in each equation of the VAR, and thus can accommodate block exogeneity.

2.3.2 Selecting the arguments of the prior

The second aspect is selecting the arguments of the prior. To do this, recall that the VAR approximation to the DSGE model in Equation (2) is conditional on a particular value of the DSGE parameters. Repeatedly sampling from the posterior of the DSGE (say 1,000 times) and constructing VAR approximations to the DSGE model, as described above, yields a set of estimates of the VAR approximation parameters 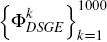(where k indexes the estimates for each sample; the index of the lag length has been suppressed) and variance-covariance matrices of the reduced-form shocks 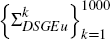.^[4] These sets of parameters can be used to inform the choice of appropriate arguments for the prior distributions.

The idea of estimating a reduced-form VAR on simulated data to obtain prior parameters was first introduced by DeJong et al (1993), although they sample from the prior of the theoretical model, rather than its posterior, and assume different prior distributions for the VAR.^[5] Also, note that in my approach the prior is more accurately described as an ‘empirical Bayes’ prior as it is constructed from the posterior of the estimated DSGE model, and therefore the same data are used to form the prior and in estimation. Sampling from the DSGE prior when constructing the VAR approximation to the DSGE model, would accord more closely with the idea of Bayesian analysis, namely that priors should be formed before seeing the data.

2.3.3 Independent Normal-Wishart prior

In order to use the independent Normal-Wishart prior I rewrite the reduced-form VAR in Equation (1), in the form outlined in Koop and Korobilis (2010).

Consider the mth equation in the VAR. This is rewritten as:

where y_mt could be either a large or small economy variable, z_mt is a (column) vector of its explanatory variables, β_m is a vector of their parameters, and u_mt is the corresponding reduced-form shock. Note that the size of z_mt will vary depending on whether y_mt is a large or small economy variable.

The n equations are stacked vertically, yielding y_t = Z_tβ + u_t, where Z_t is upper triangular with 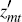on the mth row. Now stacking the T observations together vertically yields y, Z and u. The VAR can then be written as:

Priors are placed over this formulation.

The independent Normal-Wishart prior, as presented by Koop and Korobilis (2010), is:

where 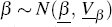, and 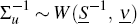, with N and W denoting the Normal and Wishart distributions and the underbar the arguments for the prior. The prior is modified by constraining the parameter space of β, Θ, to include only values for which the empirical BVAR-DSGE is stable, hence 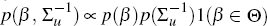, where 1 is an indicator function.

2.3.4 Estimating the arguments of the prior

Reshaping the parameter estimates 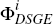into βⁱ, the prior for β, the empirical BVAR-DSGE model parameters, are centred at their sample mean. Similarly, 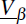is set with reference to the variance of our set of β estimates, namely:

where I is the identity matrix and 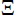is a small positive number. λ is a parameter I have introduced for further flexibility; higher values of λ cause the prior on the mean of β to have a larger variance, effectively down-weighting it relative to the data. This is just one way the prior can be loosened; others are possible. A small amount (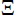) has been added to the variance of each parameter to ensure that the variance-covariance matrix is not singular.^[6] For a particular 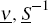is set to match the mean of .

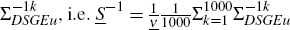There are several possible approaches to selecting λ and 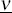. One is to simply examine plots of the prior for different values and to decide whether they appear reasonable. Another way to select them would be to examine the forecasting performance of the reduced-form empirical BVAR-DSGE model for a range of values. Finally, a natural criterion is to maximise the marginal likelihood, which can be interpreted as selecting the model (indexed by λ and 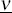) that maximises the likelihood of observing the data. Given that I will use a Gibbs sampler to simulate the posterior, a sensible way of estimating the marginal likelihood is the method of Chib (1995).^[7]

2.4 Estimating the Reduced-form Empirical BVAR-DSGE Model Posterior

Koop and Korobilis (2010) show that with the independent Normal-Wishart prior the posterior of the VAR parameters conditional on the variance-covariance matrix of the shocks and vice-versa are normally distributed, which makes them suitable for using Gibbs sampling to produce draws from the joint posterior. In particular,

where 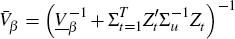, and 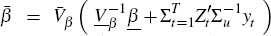, and the overbars denote that these are the arguments for the posterior. The impact of the modification is only to truncate this distribution to β draws where the VAR is stable.^[8]

Also,

where

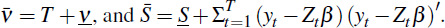
Finally, having obtained the posterior for β, its elements can be rearranged to obtain the posterior for Φ_i, enabling us to rewrite the empirical BVAR-DSGE model as in Equation (1).

Footnotes

Fernández-Villaverde et al (2007) study VAR representations of DSGE models. [2]

I simulate 40,000 observations, drop the first 100, and estimate the VAR using a seemingly unrelated regression (SUR). [3]

In an attempt to ensure that the only stochastic variation in the simulation comes from the draw of the DSGE parameters, the same seed was always used for the random number generator. When drawing the parameters, restrictions to ensure the DSGE model has a deterministic solution can be added (e.g. imposing that the Taylor principle is satisfied, namely that nominal interest rates respond sufficiently aggressively to inflation). [4]

DeJong et al (1993) mention the possibility of using independent Normal-Wishart prior, but do not do it to lessen the necessary computation. Filippeli et al (2011) also sample from the prior, rather than the posterior. [5]

I use 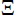= 1e⁻⁴. [6]

In the empirical example in Section 4, 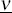is set to n + 2 and numerical difficulties were encountered when estimating the marginal likelihood. Consequently, I performed sensitivity analysis of how the results change as λ is varied. The numerical difficulties arise because for a large VAR, V_β will be very large and hence there will be many plausible values that have a very small determinant which Matlab treats as zero, even if it is positive definite. It is necessary to invert this determinant when using the Chib (1995) method, which is problematic. It might be possible to use a normalisation to circumvent this problem; exploring this is left for future research. Note that it is also necessary to account for the stability restriction when calculating the marginal likelihood. [7]

This is done in the Gibbs sampler by rejecting draws where the VAR is unstable. [8]