RDP 2013-06: Estimating and Identifying Empirical BVAR-DSGE Models for Small Open Economies 4. Empirical Application
June 2013 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 759KB
Justiniano and Preston (2010a) show that in an estimated two-country DSGE model of Canada and the United States, which includes many features typical of open economy macroeconomic models, an implausibly small amount of the variation in most Canadian series is due to shocks from the United States (less than three per cent at most forecast horizons). The model also cannot generate the correlations across the countries that exist between many of the series in the observed data. Justiniano and Preston (2010a) discuss possible reasons for these findings, including that the model has
… counter factual implications for the terms of trade and the real exchange rate, particularly in regards to their link with domestic inflation. When confronted with the data, this tension between fitting some cross-country correlations and the model's counter factual prediction for other moments is resolved in favor of the latter by shutting down international linkages. (p 72)
In this section I demonstrate that a similarly small impact is found when the Justiniano and Preston (2010a) model is estimated for Australia and the United States. In contrast, a structural empirical BVAR-DSGE model that uses the DSGE model as a prior and imposes block exogeneity finds a larger impact of foreign shocks on the small economy.
Previous structural VAR studies for Australia have often found an important role for foreign shocks, for example in determining Australian GDP. This conclusion appears to be robust to the method of analysis used. Analysing a historical decomposition of Australian output, Dungey and Pagan (2009, p 14) conclude that ‘… the most influential of the shocks are technology, preferences and the foreign sector …’; alternatively, in a forecast error variance decomposition Berkelmans (2005) finds that at the 1- and 4-quarter horizons, shocks to US GDP account for 14 and 27 per cent of the variance respectively. Using business cycle dating techniques Dungey and Pagan (2000) find that the ability of the structural VAR to capture the characteristics of the growth cycle is considerably impeded when foreign shocks are excluded.[14]
4.1 The Justiniano and Preston (2010a) Model
I provide only a brief sketch of the Justiniano and Preston (2010a) model. The log-linearised equations from their code are used, which was generously provided by Bruce Preston.[15] In each economy there are:
- households
- domestic producers
- retail firms
- a government
- a central bank.
Households consume a composite consumption good with external habits (the utility they derive from consumption depends on its level relative to lagged aggregate consumption – a ‘keeping up with the Joneses’ effect). A preference shock captures changes in preferences for consuming today relative to tomorrow. The composite good for the small economy (Australia) is composed of home-produced and foreign-produced goods, which are aggregated together using constant elasticity of substitution (CES) technology. Each of these goods themselves is a CES aggregate of many individual goods. The US consumption bundle, alternatively, is composed only of US-produced goods. Australian households may also hold Australian dollar- and US dollar-denominated bonds, with a debt-elastic premium (which includes a stochastic component) on the latter to ensure these holdings are stationary. US households hold only US dollar-denominated bonds. Australian dollar-denominated debt in Australia (and US dollar-denominated debt in the United States) is assumed to be in zero net supply. Households receive income from the interest from their bond holdings, dividends from monopolistically competitive firms, transfer payments from the government, and working. Households supply differentiated labour, which firms aggregate using CES technology. A labour disutility shock, capturing changes in preferences with respect to the supply of labour, is also included.
Retail firms in Australia import US goods. The law of one price is assumed to hold at the docks, but retailers (importers) produce differentiated goods for consumption. Domestic producers also produce differentiated goods. A standard log-linear demand function is assumed for US consumption of Australia's domestic good. In all monopolistically competitive markets, pricing is modelled using the Calvo approach, where firms and households that do not get the opportunity to reset their prices optimally in a given quarter index them to past inflation. Cost-push shocks are included for all firms.
Monetary policy is set following a Taylor rule which allows policy to depend on contemporaneous inflation, deviations of output from its steady-state level, output growth and changes in the nominal interest rate, as well as the lagged deviation of the interest rate from its steady state level. An exogenous monetary policy shock is included. Finally, all markets clear.
To summarise, there are twelve exogenous shocks, five for the United States and seven for Australia. These include, for each country:
- technology
- cost-push
- preferences
- labour disutility
- monetary policy.
The additional shocks for Australia are a cost-push shock for retail firms and the risk-premium shock, which appears in the uncovered interest parity condition. These shocks generally follow first-order autoregressive processes, with the exception of the monetary policy and the cost-push shocks, although the cost-push shock for retailers is allowed to be persistent. The Australian economy is small in the sense that its shocks cannot affect the United States.
4.2 Data
As there are twelve shocks, and in the approach to identifying the empirical BVAR-DSGE model described previously it was assumed that the number of variables equals the number of shocks, twelve observable variables are used. This is the same number used by Justiniano and Preston (2010a). I also mostly follow their definitions of the data, but use: Australian series in place of their Canadian counterparts; non-farm GDP rather than GDP per capita as the measure of output; and total, rather than average, hours worked. The precise definitions are given in Appendix C. The observed series in both countries are:
- output
- inflation
- interest rates
- real wages
- hours worked.
For Australia, changes in the real exchange rate and the terms of trade are also included. Note that the definition of the observed real exchange rate and the terms of trade are those conventionally used in Australia and are the inverse of the model definition. Consequently, the measurement equations of these variables have the observed change as the negative of their model counterparts.[16] A further aspect to note is that when Justiniano and Preston (2010a) map the data to the model, they define the terms of trade as the ratio of retail import prices to domestically produced good prices (as these are exported), whereas in the data the import prices are measured ‘at the docks’. Justiniano and Preston state that their results are not sensitive to this. In contrast, altering the measurement equations to address this yielded implausible estimates in the Australian case.
Output and real wages are linearly detrended, as in Justiniano and Preston (2010a), and hours worked are detrended.[17] The estimation sample is 1993:Q1 to 2010:Q3, noting that inflation targeting commenced in Australia in 1993:Q1.
4.3 DSGE Posterior
The priors for the large economy are based on those used by Justiniano and Preston (2010a). I deviate slightly for the priors on the exogenous processes. They state the priors include ‘… a “tilt” towards the foreign block disturbances, which are assumed twice as volatile and more persistent than their domestic counterparts’ (p 67). I remove this tilt as, intuitively, it is difficult to conceive why a large country, namely the United States, would be more volatile. For the small economy I draw on Justiniano and Preston (2010b), but do not use a structural model for the large economy. I also deviate from the priors of Justiniano and Preston (2010a, 2010b) in a number of ways. First, I fix the inverse Frisch elasticity, which governs the labour supply response to changes in the real wage, as estimation tended to yield very small values. Second, I assume that the small economy Taylor rule does not include the exchange rate; Lubik and Schorfheide (2007) find little role for it.
Table 1 below shows the prior and posterior values for the DSGE parameters. The notation of the parameters follows Justiniano and Preston (2010a).[18] A random-walk Metropolis-Hastings chain of one million observations was used to simulate the posterior. The first 85 per cent of the chain was dropped to ensure that it had converged to a stationary distribution. To check that convergence had occurred a second chain was also run.
| Australia | |||||||
|---|---|---|---|---|---|---|---|
| Coefficient Description | Prior | Posterior | |||||
| Density | Mean | Std dev | Mean | 90% HPD | |||
| h | Habits | B | 0.5 | 0.25 | 0.18 | 0.03–0.32 | |
| σ | Intertemporal ES | N | 1.0 | 0.4 | 1.40 | 0.93–1.83 | |
| λ* | Elasticity foreign demand | G | 1.5 | 0.5 | 0.38 | 0.24–0.54 | |
| η | Elasticity H-F goods | G | 1.5 | 0.75 | 0.34 | 0.13–0.55 | |
| ρa | Technology | B | 0.8 | 0.1 | 0.91 | 0.86–0.96 | |
| ρg | Preferences | B | 0.8 | 0.1 | 0.81 | 0.73–0.89 | |
| ρcp, F | Cost-push imports | B | 0.5 | 0.25 | 0.60 | 0.39–0.81 | |
| ρrp | Risk premium | B | 0.8 | 0.1 | 0.95 | 0.92–0.99 | |
| ρL | Labour disutility | B | 0.8 | 0.1 | 0.52 | 0.40–0.64 | |
| θi | Taylor rule, smoothing | B | 0.5 | 0.25 | 0.80 | 0.74–0.86 | |
| αH | Calvo domestic prices | B | 0.5 | 0.1 | 0.55 | 0.46–0.63 | |
| αF | Calvo import prices | B | 0.5 | 0.1 | 0.56 | 0.45–0.68 | |
| αW | Calvo wages | B | 0.6 | 0.1 | 0.29 | 0.22–0.36 | |
| θπ | Taylor rule, inflation | G | 1.5 | 0.3 | 2.17 | 1.78–2.59 | |
| θdy | Taylor rule, growth | G | 0.25 | 0.13 | 0.53 | 0.26–0.78 | |
| θy | Taylor rule, output | G | 0.25 | 0.13 | 0.10 | 0.04–0.16 | |
| γH | Indexation, domestic | B | 0.5 | 0.2 | 0.63 | 0.42–0.84 | |
| γF | Indexation, imports | B | 0.5 | 0.2 | 0.44 | 0.18–0.71 | |
| γW | Indexation, wages | B | 0.5 | 0.2 | 0.57 | 0.27–0.90 | |
| Standard deviations | |||||||
| σa | Technology | IG | 1 | 1 | 0.79 | 0.69–0.91 | |
| σg | Preferences | IG | 1 | 1 | 1.18 | 0.79–1.56 | |
| σcp, H | Cost-push domestic | IG | 0.25 | 1 | 0.70 | 0.57–0.83 | |
| σcp, F | Cost-push foreign | IG | 1 | 1 | 2.69 | 1.68–3.74 | |
| σrp | Risk premium | IG | 1 | 1 | 0.47 | 0.35–0.59 | |
| σn | Labour disutility | IG | 5 | 1 | 5.96 | 4.23–7.66 | |
| σi | Monetary policy | IG | 0.25 | 0.25 | 0.15 | 0.12–0.18 | |
| Calibrated | |||||||
| φ | Inverse Frisch | 1 | |||||
| β | Discount factor | 0.99 | |||||
| χ | Interest debt elasticity | 0.01 | |||||
| τ | Openness | 0.185 | |||||
| θ | Elasticity of substitution | 8 | |||||
| United States | |||||||
| Coefficient Description | Prior | Posterior | |||||
| Density | Mean | Std dev | Mean | 90% HPD | |||
| h* | Habits | B | 0.5 | 0.1 | 0.18 | 0.51–0.74 | |
| σ* | Intertemporal ES | N | 1.0 | 0.4 | 0.92 | 0.64–1.20 | |
| ρa* | Technology | B | 0.8 | 0.1 | 0.89 | 0.84–0.94 | |
| ρg* | Preferences | B | 0.8 | 0.1 | 0.89 | 0.83–0.94 | |
| ρL* | Labour disutility | B | 0.8 | 0.1 | 0.65 | 0.51–0.79 | |
| θi* | Taylor rule, smoothing | B | 0.8 | 0.1 | 0.88 | 0.85–0.91 | |
| αH* | Calvo prices | B | 0.6 | 0.1 | 0.90 | 0.87–0.93 | |
| αw* | Calvo wages | B | 0.6 | 0.1 | 0.39 | 0.32–0.47 | |
| θπ* | Taylor rule, inflation | N | 1.8 | 0.3 | 1.90 | 1.48–2.32 | |
| θdy* | Taylor rule, growth | N | 0.3 | 0.2 | 0.80 | 0.58–1.01 | |
| θy* | Taylor rule, output | G | 0.25 | 0.13 | 0.06 | 0.02–0.09 | |
| γH* | Indexation, prices | B | 0.5 | 0.2 | 0.42 | 0.23–0.61 | |
| γw* | Indexation, wages | B | 0.5 | 0.2 | 0.56 | 0.25–0.88 | |
| Standard deviations | |||||||
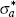 |
Technology | IG | 1 | 1 | 0.63 | 0.55–0.73 | |
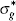 |
Preferences | IG | 1 | 1 | 2.79 | 1.79–3.57 | |
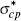 |
Cost-push | IG | 0.25 | 1 | 0.24 | 0.20–0.27 | |
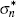 |
Labour disutility | IG | 5 | 1 | 6.22 | 4.20–8.20 | |
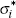 |
Monetary policy | IG | 0.25 | 0.25 | 0.12 | 0.10–0.13 | |
| Calibrated | |||||||
| φ* | Inverse Frisch | 1 | |||||
| β* | Discount factor | 0.99 | |||||
| θ* | Elasticity of substitution | 8 | |||||
| Notes: Prior distributions are B – Beta, N – Normal, G – Gamma, IG – inverse Gamma; HPD denotes highest probability density; ES denotes elasticity of substitution; H-F denotes home-foreign | |||||||
The estimates of the preferences of the representative Australian consumer differ somewhat from those of previous studies: the intertemporal elasticity of substitution is surprisingly high (1.40), and the value of the habits parameter h suggests that there is only a limited role for external habits, which is at odds with the findings of Justiniano and Preston (2010b) (0:33) and Jääskelä and Nimark (2011) (0.76).[19] The estimated elasticity of foreign demand for Australian goods (0.38) is less than was found by Justiniano and Preston (2010b) (0.58), although given the strong demand from China for Australian resource exports in recent years, a lower elasticity may be plausible.
The Calvo parameters for domestically produced goods are lower than those of Justiniano and Preston (2010b), and are considerably smaller than generalised method of moments estimates for Australia (e.g. Kuttner and Robinson (2010)). One factor may be that there is only one good produced in the model, which can either be consumed or exported. Over the second half of the 2000s, export prices grew by considerably more than consumer prices, which is reflected in the rise in the terms of trade. The model appears to reconcile this tension by making prices relatively flexible. Wages are estimated to be much more flexible than was found by Jääskelä and Nimark (2011) (a Calvo parameter of 0.29, compared with 0.63). There is estimated to be considerable indexation of prices and wages, particularly for domestically produced goods (0.63). These figures, while broadly comparable with those found by Jääskelä and Nimark, are sufficiently large to raise the question of whether it is truly indexation which is being captured.
The estimated Taylor rule for Australia exhibits a similar degree of persistence to those of Justiniano and Preston (2010b) and Jääskelä and Nimark (2011), but reacts more aggressively to inflation.[20] A one standard deviation quarterly monetary policy shock is estimated to be around 15 basis points, which is smaller than was found by Justiniano and Preston (2010b) but, as their estimation sample covers more than just the inflation-targeting period, this seems plausible.
Turning to the exogenous processes, it is apparent that the standard deviation of the labour disutility shock in Australia is very large. One possible explanation is that, as the model has both a simple production and financial structure, it uses this shock to explain much of the decrease in output during the global financial crisis. This is also evident in the estimate for the United States. The standard deviations of the labour supply shocks in both countries are imprecisely estimated, despite a relatively tight prior being used. Compared to the findings of Justiniano and Preston (2010a) most of the estimates of the other US parameters are similar, although I find wages to be much more flexible, with an estimated Calvo parameter of 0.39, compared to 0.87, but indexation appears to be more prevalent. The high Calvo parameter for goods prices and the degree of indexation found imply quite a flat Phillips curve, although not as flat as that estimated by Justiniano and Preston (2010a).
The BVAR-DSGE model estimated using the methodology of Del Negro and Schorfheide (2004) yields different estimates of the DSGE parameters to those presented above and are in Appendix D. The differences arise because the DSGE and BVAR-DSGE parameters are jointly estimated in the Del Negro and Schorfheide (2004) approach. Another noticeable difference is that the standard deviations of the shocks obtained from the Del Negro and Schorflheide methodology for both economies tend to be smaller.
4.4 Empirical BVAR-DSGE Model Results
One of the main conclusions of Justiniano and Preston (2010a) is that the DSGE model does not capture the impact of the large economy shocks on the small economy, and so I do not match those impulse responses. Instead, I select QL to match the impact of large economy shocks on the large economy variables alone.[21]
In order to examine the dynamics of the empirical BVAR-DSGE model, and how they differ from those of the DSGE model, I now present the estimated responses to several domestic and foreign shocks. The main point of this section is to illustrate some of the dynamics of the empirical BVAR-DSGE model, particularly with respect to the impact of foreign shocks on the Australian economy, and how they differ from those of the DSGE model.
In this section, BVAR-DSGE refers to the estimates obtained using the methodology of Del Negro and Schorfheide (2004), and BVAR to those from the empirical BVAR-DSGE model. Recall that λ is a parameter that was introduced to allow for some judgment about the variance of the prior in the BVAR parameters, and therefore how tightly the prior is held. Examining plots of the posterior distributions suggests that for λ = 1 the prior is very tightly held. This could partly reflect the fact that the posterior of the DSGE model was used to construct the prior for the BVAR, but it is also tightly held if I sample from the prior of the DSGE model, which suggests that the structure of the DSGE model itself places considerable restrictions on the reduced-form BVAR. Consequently, the impulse responses are also shown in the following figures for when the prior is relaxed, using λ = 100. Note that the size of a one standard deviation shock varies across the models.
In both the BVAR-DSGE and the BVAR, following Justiniano and Preston (2010a), the terms of trade and the real exchange rate are included in first differences. In the DSGE model this can be motivated by concerns about these variables possibly being non-stationary in the data, despite the predictions of the model. However, unlike the DSGE case, using first differences in the BVAR-DSGE and the BVAR models means that shocks may have a permanent impact on these variables. An alternative is to include these variables as deviation from trend, constructed outside the model (for example, using a Hodrick-Prescott filter). Another approach, which is probably preferable to off-model filtering, would be to introduce permanent shocks into the DSGE model itself.[22]
4.4.1 Impulse responses – Australian monetary policy shock
The impulse responses for most of the observed variables from the BVAR (with either value of λ) and the DSGE model, are similar for an Australian monetary policy shock (Figure 1). The size of the quarterly monetary policy shock in the DSGE model is approximately 15 basis points. In all four models, the monetary policy shock leads to an immediate fall in output, which is in contrast to Dungey and Pagan (2000), where they restrict the cash rate to affect output with a lag. There is also a sizable contemporaneous appreciation of the real exchange rate and fall in inflation.
The monetary policy tightening in Australia leads to a rise in the terms of trade (the ratio of export prices to import prices). This occurs in the DSGE model in the short term because the decline in inflation in domestically produced goods (exports) is less than it is for imports. While the degree of price stickiness for both domestic good producers and retailers is similar, the marginal costs of domestic goods are also sticky due to nominal wage rigidities, whereas this is not the case for imports.
One aspect of the Justiniano and Preston (2010a) DSGE model is that the terms of trade is treated as endogenous to the small economy. This is because, while the small economy cannot affect the world (US) price of its imports, importers in this model produce differentiated goods from these imports, and price them with a mark-up. When the model is mapped to the data, as previously mentioned, import prices in the terms of trade are equated to the retail price, rather than the ‘at-the-dock’ price. Australian domestic good producers also have some market power, and these goods are exported.
The greatest divergences between the impulse responses from the Justiniano and Preston (2010a) model and those from the BVAR models are with respect to the labour market variables. In the DSGE model there is a decline in the real wage and hours worked following a monetary policy shock, which is not surprising given the simple linear production structure for domestic goods where labour is the only input (apart from technology). The BVAR estimates, which relax this, find a smaller decline in both hours worked and the real wage.
4.4.2 Impulse responses – foreign shocks
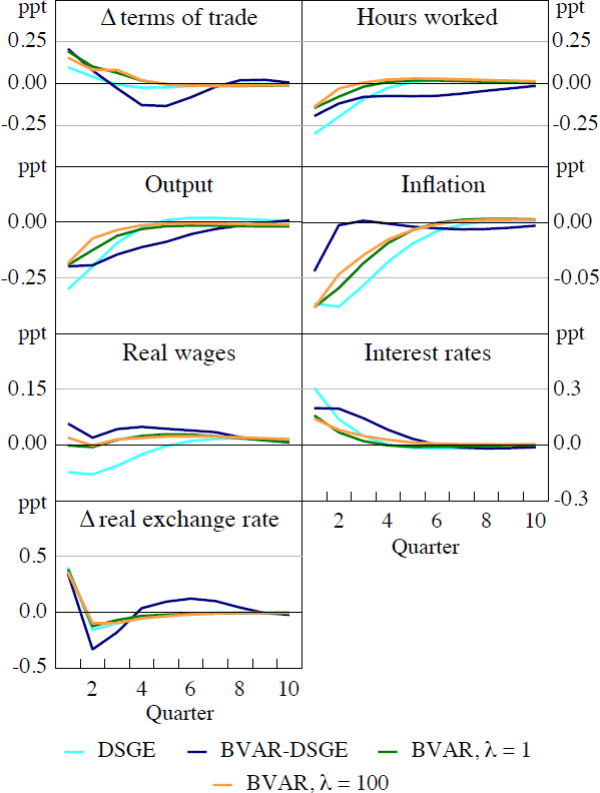
Turning now to the foreign shocks, I consider first a positive productivity shock and its impact on the US economy (Figure 2). The increase in output estimated by the BVARs is greater than that estimated by the DSGE model, whereas for most time horizons the fall in inflation is slightly less. In all models, hours worked decline in response to the productivity shock. The decrease in inflation in the DSGE model is small, reflecting the flatness of the Phillips curve, and in the BVAR models it is not very persistent, especially as the prior is relaxed. After an initial increase, the impact on output in the BVAR-DSGE model gradually becomes negative, which is difficult to rationalise as it also predicts the largest fall in the interest rate occurs after around one year.
The impact of a positive US productivity shock on the Australian variables is surprising. The estimates from the DSGE model suggest that, for all variables, the impact is slight. In contrast, the BVAR models, with either λ suggest that the real exchange rate appreciates and the terms of trade decline. Intuitively one might have expected Australia's terms of trade to improve, given that import prices should have fallen due to the nominal exchange rate appreciation, however, domestic inflation (and hence export prices), decreases after an initial rise. This could reflect the surprisingly large decreases in the interest rate, which may be an attempt to mitigate the decline in output (possibly stemming from a decrease in the volume of exports).
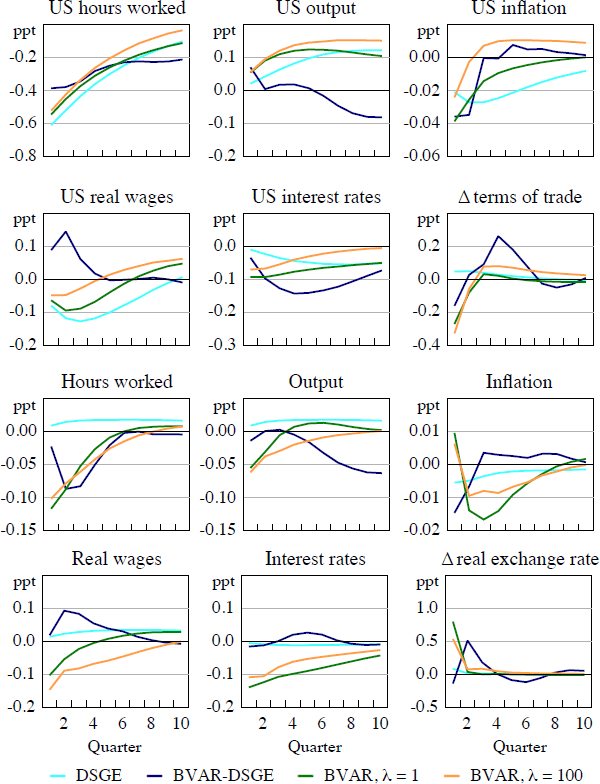
A positive US preference shock, which is an example of a demand shock, leads to a rise in US hours worked and output (Figure 3). While the estimated initial impact for both variables is very similar for the DSGE and the BVAR models in the near term, loosening the prior appears to make these effects more persistent to a surprising extent. These models all suggest that there is little impact on US inflation, which is probably due to the flatness of the Phillips curve in the prior, although an accompanying factor is that the shock causes an aggressive monetary policy tightening.
Considering now the impact on Australia of a positive US preference shock, the predictions for the terms of trade are mixed. Intuitively one would expect such a shock to raise demand for Australia's exports and thus increase the terms of trade. The DSGE and BVAR-DSGE models suggest that the terms of trade does increase contemporaneously, whereas the BVAR models predict an initial decline and then some modest growth. The models all suggest that there is a persistent increase in Australian output, meaning that the foreign demand shock increases the volume of exports by more than their value. This is surprising given Australia's recent history of strong growth in the terms of trade and subdued growth in the volume of exports.[23] The magnitude of this effect is greater in the BVAR models than in the DSGE model, and it increases with λ. Accompanying the rise in output are increases in hours worked and real wages, together with a small monetary policy tightening. The impact on inflation is slight; although output increases there is also a substantial real appreciation in the exchange rate.
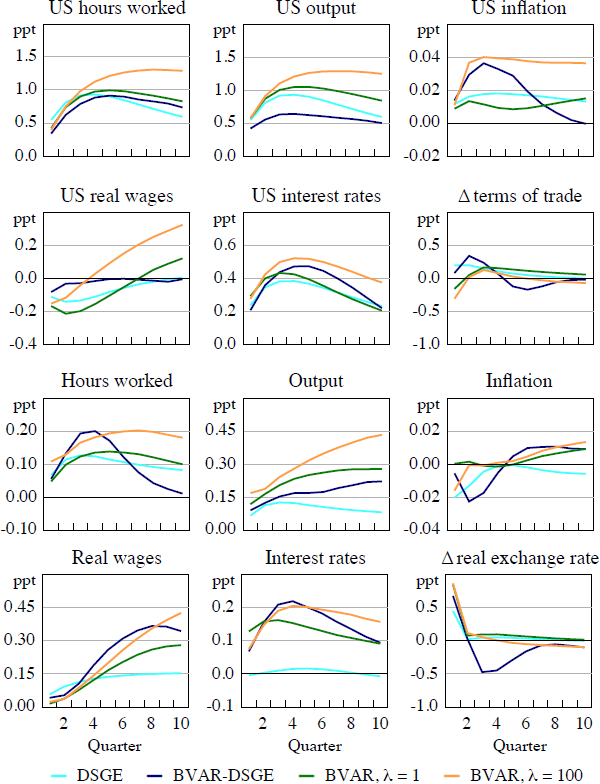
The impact of a positive US monetary policy shock on the US variables are estimated to be similar by the DSGE and the BVAR models, although output declines by slightly more in the latter (and more so when λ = 100) (Figure 4). The decline in US inflation is very small. A larger, albeit still small, impact is estimated in the BVAR-DSGE model. Turning to the impact on Australia, the BVAR models suggest a depreciation in the real exchange rate, a response that is predicted by uncovered interest parity. The decline in the terms of trade predicted by the BVAR models is of a comparable magnitude to that in the DSGE model. A fall in output is predicted by all of the models, although it is more persistent in the BVARs. Intuitively, one would expect hours worked to decline as output falls, however, this only occurs in the DSGE model, with more sizable falls in real wages mitigating its decline in the BVARs. The estimated impact on Australian inflation differs across the models, with the DSGE model predicting a small increase, in part due to the real exchange rate depreciation, whereas the BVAR models suggest the opposite, perhaps as they predict a larger decline in output.
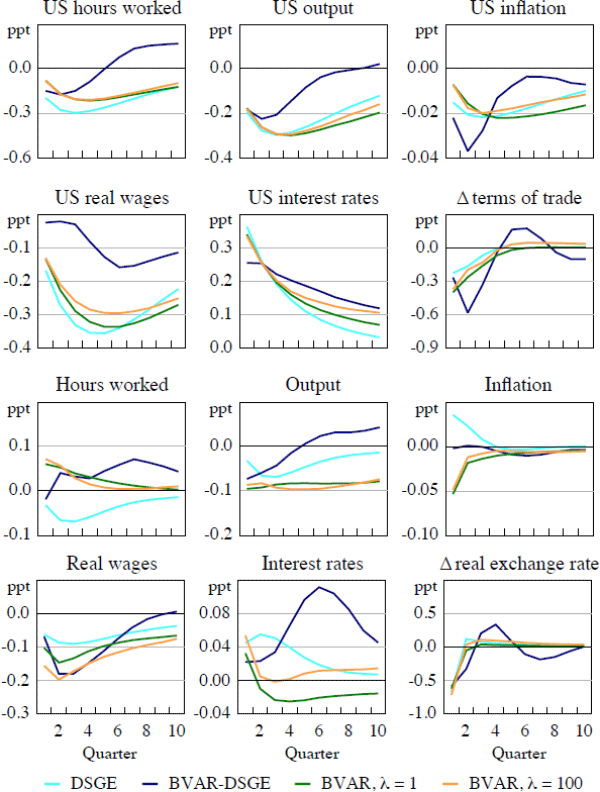
4.4.3 Forecast error variance decomposition
One of the main findings of Justiniano and Preston (2010a) is that the estimated DSGE model suggests that US shocks account for an implausibly small share (generally less than 3 per cent) of the variation in key Canadian series at various forecast horizons. Table 2 shows that a similar result is obtained when the DSGE model is applied to Australia, although the share is larger.
| 1-quarter horizon | 4-quarter horizon | 8-quarter horizon | ||||||
|---|---|---|---|---|---|---|---|---|
| DSGE | B-D | DSGE | B-D | DSGE | B-D | |||
| Δ Real exchange rate | 4.5 | 18.5 | 4.5 | 18.6 | 4.5 | 18.7 | ||
| Δ Terms of trade | 4.1 | 11.4 | 5.4 | 13.3 | 4.9 | 14.1 | ||
| Output | 1.2 | 19.9 | 2.7 | 20.2 | 3.2 | 26.7 | ||
| Interest rate | 0.6 | 31.5 | 0.8 | 34.0 | 0.7 | 35.2 | ||
| Inflation | 1.1 | 15.9 | 1.1 | 14.7 | 1.0 | 17.2 | ||
| Real wage | 1.0 | 8.3 | 2.8 | 8.7 | 4.8 | 12.4 | ||
| Hours worked | 0.9 | 12.2 | 3.3 | 15.6 | 4.9 | 20.0 | ||
| Notes: DSGE evaluated at mean of the posterior parameter values; B-D denotes the empirical BVAR-DSGE model and is the median share; B-D has 2 lags and λ = 1 | ||||||||
The estimates in Table 2 suggest that the contribution of foreign shocks to the forecast error variance of the terms of trade is less than five per cent at most horizons.[24] Alternatively, the empirical BVAR-DSGE model, denoted in Table 2 as B-D, estimates that between 10 and 15 per cent of the variation in changes in the terms of trade is due to foreign shocks, which, while much higher than suggested by the DSGE, is still implausibly small. This may be because the foreign sector is being modelled as the United States, whereas in recent years strong demand for commodities from China has been a key factor explaining the rapid rise in Australia's terms of trade. The empirical BVAR-DSGE model suggests that US cost-push shocks play a larger role in explaining the variation in forecast errors in the terms of trade than in the DSGE model.
Turning to the real exchange rate, the BVAR with λ = 1 suggests that around 19 per cent of fluctuations in the forecast error of changes in the real exchange rate are due to foreign variables, primarily reflecting US cost-push shocks and technology shocks (Table 3). Only around 20 per cent of fluctuations in Australian output are due to foreign shocks, possibly as the real exchange rate is acting as a buffer. The variable with the highest contribution from US shocks – around 30 to 35 per cent – is the interest rate, reflecting foreign cost-push and, to a lesser extent, preference and technology shocks. One interpretation of cost-push shocks is that they capture global inflation surprises. Interestingly, a recursive VAR estimated using OLS finds a similarly large role for foreign shocks for explaining the interest rate. One possibility is that this reflects the rapid series of interest rate cuts that occurred in Australia during the global financial crisis. There is little variation in these shares as the forecast horizon increases, although the role of foreign shocks for output and the terms of trade does increase at longer horizons.
| DSGE | BVAR | |||
|---|---|---|---|---|
| λ = 1 | λ = 10 | λ = 100 | ||
| 4-quarter horizon | ||||
| Δ Real exchange rate | 4.5 | 18.6 | 17.8 | 18.9 |
| Δ Terms of trade | 5.4 | 13.3 | 13.7 | 16.5 |
| Output | 2.7 | 20.2 | 25.6 | 28.5 |
| Interest rate | 0.8 | 34.0 | 30.3 | 33.2 |
| Inflation | 1.1 | 14.7 | 16.2 | 18.5 |
| Real wage | 2.8 | 8.7 | 12.0 | 16.3 |
| Hours worked | 3.3 | 15.6 | 15.7 | 17.2 |
| 10-quarter horizon | ||||
| Δ Real exchange rate | 4.5 | 18.7 | 17.8 | 19.4 |
| Δ Terms of trade | 4.9 | 14.2 | 14.6 | 17.8 |
| Output | 3.4 | 30.0 | 41.7 | 47.5 |
| Interest rate | 0.7 | 35.5 | 33.0 | 39.0 |
| Inflation | 1.0 | 18.1 | 19.7 | 22.3 |
| Real wage | 5.6 | 15.1 | 22.1 | 28.2 |
| Hours worked | 5.4 | 21.4 | 26.2 | 25.1 |
| Notes: DSGE evaluated at mean of the posterior parameter values; BVAR is the median share and has 2 lags | ||||
Footnotes
The nature of these foreign shocks differ across the models. For example, Dungey and Pagan (2000) find that foreign financial shocks are particularly important. [14]
The equations are listed in Appendix B. [15]
That is, an increase in the observed real exchange rate is an appreciation. A further difference with Justiniano and Preston (2010a) is that I use a trade-weighted, rather than a bilateral, measure of the exchange rate. The observed terms of trade are calculated as the ratio of export to import prices. [16]
Justiniano and Preston (2010a) extract a common linear trend, whereas I detrend each series individually. [17]
The elasticity of substitution is between individual consumption goods (for Australia both domestic and imported) and types of labour. These are necessary to facilitate price and wage stickiness. [18]
All figures referring to this paper or Jääskelä and Nimark (2011) are estimates for the mean, whereas those from Justiniano and Preston (2010a, 2010b) are for the median of the posterior. The estimation samples are: Justiniano and Preston (2010b) 1984:Q1–2007:Q1; Jääskelä and Nimark (2011) 1993:Q2–2007:Q3. [19]
Note that the inflation, output and real exchange rate terms in the Taylor rule in Jääskelä and Nimark (2011) are lagged by one period, whereas in the other models they are not (if included). [20]
For the Gibbs sampler I take 30,500 draws, and discard the first 500. [21]
The estimate of the trend from, for example, a Hodrick-Prescott filter, may be inconsistent with that implied by the model and using the corresponding gap series could create econometric problems (Fukač and Pagan 2010). Alternatively, the typical way a permanent shock is introduced into a small open economy model is by introducing a common technology shock to both countries that is non-stationary. This will not produce a non-stationary real exchange rate or terms of trade, but instead predicts that many real variables, such as output in both countries, will be cointegrated, although the data do not support this. For further discussion on this see Justiniano and Preston (2010a) for Canada and Dungey and Pagan (2009) for Australia. [22]
The latter partially reflects the depletion of existing oil and gas fields with expectations of stronger growth resulting from very high resource sector investment over recent years (Plumb, Kent and Bishop 2013). [23]
As discussed previously, the terms of trade for Australia is not exogenous in this model. [24]