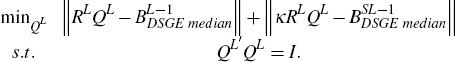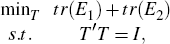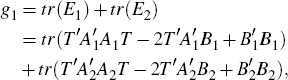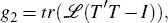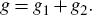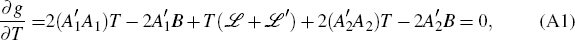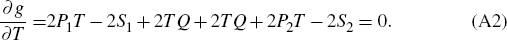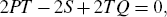RDP 2013-06: Estimating and Identifying Empirical BVAR-DSGE Models for Small Open Economies Appendix A: Identifying the Large Economy
June 2013 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 759KB
This appendix shows that the problem of selecting QL to match the impulse responses of the large and small economies to large economy shocks can be obtained in the same way as when only the impact on the large economy is considered, with some matrices redefined.
The problem is
The solution closely follows Schönemann (1966). In this appendix I adopt his
notation, which is different to that throughout the rest of the paper. Let
T ≡ Q, 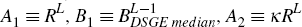 , and
, and 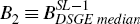 . I can then define
two residual matrices E1 = A1T
− B1 and E2 = A2T
− B2. The problem can then be rewritten as:
. I can then define
two residual matrices E1 = A1T
− B1 and E2 = A2T
− B2. The problem can then be rewritten as:
where tr(.) denotes the trace.
The objective function is:
using that tr(A) = tr(A′).
The constraint can be rewritten as:
where ℒ is a matrix of Lagrange multipliers. The Lagrangian, g, then is:
Partially differentiating g with respect to the elements of T provides the first order conditions (apart from the constraint):
using the symmetry of 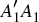 and
and 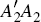 ,
and where 0 is a matrix.
,
and where 0 is a matrix.
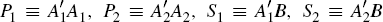 and
and 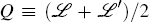 .
Equation (A1) can then be rewritten as
.
Equation (A1) can then be rewritten as
Now P ≡ P1 + P2 and S ≡ S1 + S2. Note that as the sum of two symmetric matrices is symmetric, P is symmetric. Equation (A2) can then be rewritten as
and hence
Equation (A3) is the same as Equation (1.9) in Schönemann (1966). This shows
that these first order conditions are the same as those to the original problem,
with some of the matrices redefined. Consequently the solution is the same;
the optimal T, T*, is obtained by a singular-value decomposition of S,
which yields 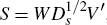 , and setting T* = WV′.
In the notation used in this paper S corresponds to TL,
which equals
, and setting T* = WV′.
In the notation used in this paper S corresponds to TL,
which equals 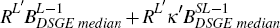 . A singular value decomposition of TL
yields
TL = UL WL VL′,
and the solution for T* above corresponds to QL*
= UL VL′.
. A singular value decomposition of TL
yields
TL = UL WL VL′,
and the solution for T* above corresponds to QL*
= UL VL′.