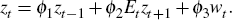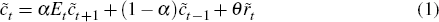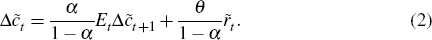RDP 2011-04: Assessing Some Models of the Impact of Financial Stress upon Business Cycles 2. Model Designs

It is useful to think about models to handle financial conditions in two stages. First, a ‘core’ model needs to be specified that details how expenditures are determined. Second, this is augmented with a sub-model involving the financial sector and showing how the latter impacts upon financial variables in the core model. This augmentation generally involves the introduction of a financial intermediary (FI) which responds to the demand for credit by supplying it. The FI may be introduced explicitly and a detailed description is given of its operation, although often only a simple summary of what governs the demand for and supply of credit is provided.

2.1 The Core Macroeconomic Model

The selection of a core model will always be controversial and a range of possibilities exist, which are described in Fukač and Pagan (2010). Some, for example Muellbauer (2010), seem to have a preference for what have been termed second generation models in Fukač and Pagan (2010). These provide a set of equations describing macroeconomic outcomes which are guided by theory to varying degrees, rather than being explicitly based on, say, optimizing behaviour by agents. This greater flexibility may allow important features of the economy or the data to be incorporated more easily.

Alternatively, fourth generation or Dynamic Stochastic General Equilibrium (DSGE) models place more weight on being consistent with theory. A popular core model for quite a few macroeconomic investigations has been the DSGE model of Smets and Wouters (2007) (termed SW hereafter). This model describes the determination of consumption, investment, wages, inflation, monetary policy and the supply side, and is derived from optimizing behaviour by agents. There are, however, clearly missing items in the model that are likely to be important to macroeconomic outcomes, for example government expenditure is strictly exogenous. Each of the structural equations for consumption, investment, the price of capital, inflation and wages have effects from expectations about the future as well as past events (z_t−1) and other model variables (w_t), that is, they have the structure

In some cases ϕ₁ + ϕ₂ = 1. Identities are also present and supply is constrained by a production function.

2.2 Expenditure Components Influenced by Financial Factors

To augment the core model it is useful to ask what items of expenditure the financial sector would impact upon. Four broad areas are suggested.

1. Fixed investment by firms.
2. Residential investment by households.
3. Consumer durable expenditures by households.
4. Consumption of goods and services by households.

We review work on how financial conditions have been introduced so as to have an impact upon the expenditures above. Mostly, core models do not specifically distinguish these categories, dealing only with aggregate investment and consumption, so we also briefly discuss how some have been introduced into macroeconomic models. Moreover, the four types of expenditures listed are not an exhaustive list of those that financial conditions can have an impact upon. For example, the availability of credit for international trade was an issue during the GFC. Similarly, there is extensive use of credit for the financing of inventories, and in Australia during the GFC car dealers had difficulty in obtaining credit to hold the vehicles on display in their car yards. Even in more normal times, inventories need to be financed for the period of time between delivery and sale. Trade credit is also needed in order to pay for raw materials and even labour. But there has been less empirical work on these latter elements than on the four areas listed above.

2.2.1 Fixed investment

Fixed investment is the area where introducing financial effects is by far the best developed, typically using the financial accelerator mechanism. A notable example of this approach is Bernanke, Gertler and Gilchrist (1999). It implicitly involves an FI, which can be thought of as taking deposits from the household sector and then lending to the business sector (usually referred to as entrepreneurs) that is in need of credit to finance fixed investment. The credit-using agents are taken to be less patient than the lending agents.

In a model with a financial accelerator, credit comes at a cost that is a premium over internal financing, namely the external finance premium. This premium results from the fact that there is asymmetric information between the borrower and the FI, typically about the realised return on capital. The external finance premium therefore governs the amount of credit that can be obtained, and so it is necessary to model its determinants. Mostly the premium is simply taken to be increasing in the degree of leverage.^[1] Therefore, increasing amounts of credit are costly, and this impacts on real and nominal quantities. Shocks which impact on the net worth (leverage) of the firm will alter the external finance premium, potentially amplifying the impact of the shock. Because the emphasis in this extension is on variations in the price of credit reflecting the credit-worthiness of the borrower, the external premium equations are often augmented with a shock that is intended to capture unrelated variations in supply, that is, the equation is more of a reduced-form than a structural equation. This is the strategy used in Gilchrist et al (2009).

Because there are no directly observed series on the external finance premium, empirical work either requires a proxy to be constructed or the external finance premium to be left unobservable. Gilchrist et al (2009) take data on the spreads between medium risk long-maturity US corporate bonds and the 10-year Treasury yield to be a measure of this premium. They also utilise data on the leverage ratio of US firms, and this series helps to estimate the elasticity of the external finance premium to the leverage ratio.

2.2.2 Residential investment

The events preceding the GFC led to an interest in the role of housing investment in the business cycle. Indeed some see it as the key to the business cycle, such as Leamer (2007). But inspection of the cycle data has to cast doubt on such a position. The duration of the US residential investment cycle is quite short, on average around 12 quarters, which is around half the length of the business cycle. This reflects that the average growth rate in residential investment is around half that of GDP, while the volatility is about five times as high. Thus negative growth in residential investment occurs relatively frequently, and often results in a turning point in the series. These differences, combined with residential investment's small share of output mean that, even if one had the knowledge that residential investment was in a contraction, the probability of predicting an NBER-defined recession would just rise to 0.27 from its unconditional probability of 0.16.^[2] Thus it is hard to subscribe to Leamer's viewpoint that housing is the business cycle. This is not to deny that it has a role, but it is not an exclusive one.^[3]

A number of papers have developed macroeconomic models including residential investment. Iacoviello and Neri (2010) augment a standard macroeconomic model by adding a second production sector, building upon the work of Davis and Heathcote (2005). In Iacoviello and Neri, the first sector produces consumption, intermediate and investment goods with capital and labour, while the other creates new houses using capital, labour, intermediate goods and land. Land, which is assumed to be in fixed supply, together with adjustment costs to capital, creates some sluggishness in the supply of housing. Iacoviello and Neri (2010) also allow for different trend rates in technology growth across sectors. They demonstrate that their model can capture some observed correlations in the data (such as a strong correlation between detrended residential investment and output) and that housing-specific shocks, namely technology and preference shocks, account for around one-quarter of the fluctuations in residential investment and house prices. Iacoviello and Neri acknowledge that the housing preference shocks may be capturing other unmodelled factors shifting housing demand rather than changes in preferences.

Apart from the sectoral disaggregation of production, the Iacoviello and Neri (2010) model features the idea that housing could serve as a collateral asset to finance either investment or consumption. This was introduced in Iacoviello (2005), and we discuss further in Section 2.3 on the supply of credit. Alternatively Aoki, Proudman and Vlieghe (2004) introduce a Bernanke et al (1999) style financial accelerator mechanism by making the rate at which homeowners can borrow depend on their net worth. However, production of new housing in Aoki et al (2004) is very simply modelled, with the only inputs being the existing housing stock and the consumption good.

Beneš et al (2009) is notable for augmenting a core model to capture housing investment in an open, rather than closed, economy.^[4] Credit is required by the household sector to purchase housing and the FI raises funds in a foreign market. These are then loaned out to the domestic market. Consequently, the external premium reflects the difference between the domestic and foreign interest rates.

2.2.3 Consumption

In the core macroeconomic model, the consumption Euler equation (with habit persistence) takes the form (after log-linearization)

where r_t is the real interest rate and tildes denote log departures from a steady state position. Preference shocks may also appear in the structural equation.

Equation (1) can be written as

The term 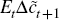varies with the model, and in general there will be a large number of influences on expected future consumption growth. When the model is extended to incorporate financial influences the number of factors would grow. The introduction of borrowing constraints, which is described below, modifies the Euler equation for credit-constrained households further; for example, nominal, rather than just real interest rates, become important.

Alternative approaches to assessing the impact of credit conditions on consumption, rather than using a general equilibrium model, do exist. One example is Aron et al (2010), who focus on a ‘solved-out’ consumption function, rather than the Euler equation; the 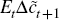term in Equation (2) does not appear but is replaced by a number of factors involving liquid assets, housing wealth etc. The coefficients on some of these terms are made functions of a credit conditions index that is constructed differently for each of the countries they examine, but which essentially extracts a common factor from many series that contain some information on the tightness of credit. Of course the credit conditions index used by Aron et al is generally constructed from information that is not in the augmented model, but series encapsulating that information might be employed when estimating it by adding them to the observation equations relating to the unknown external finance premium. If a number of series representing credit conditions are added a common factor among them would then be extracted. Another difference is that the core model described above is linear in logs, and so there would be no interaction terms with whatever is used to represent financial stress in the model. Again this might be emulated by performing a second-order approximation of the core model, as that will produce interaction terms involving covariances.

2.3 The Supply of Credit

In addition to the factors discussed above that influence the demand for credit, and its price, there may also be constraints on the quantity of available credit. There is no doubt that credit rationing was a primary financial mechanism in the models of the 1960s and 1970s, as it reflected the regulated financial markets then in operation. Since that time, however, the amount of credit supplied by financial intermediaries has been more endogenously determined. Nevertheless, some constraints still operate, reflecting asymmetric information. In particular, it is often assumed that credit is only supplied if there is an adequate amount of collateral posted by the borrower. Consequently the value of the collateral asset determines the quantity of credit available, whereas the financial accelerator mechanism alters the price of credit. The collateral could be any asset which serves that purpose, such as the capital stock, but often a new asset is introduced that may be demanded by either entrepreneurs/firms, households, or both. Sometimes this asset is referred to as ‘housing’, ‘land’ or ‘real estate’, since the main component of the value of a house is generally the land value, but often most of its attributes are the same as a durable consumption good. Households consume housing services and entrepreneurs may use the asset in production, and so it may have a role in producing output as well as facilitating the acquisition of credit.

Agents in these models typically are split into those who are subject to a borrowing constraint and those who aren't. The latter are taken to be patient and so have a lower discount rate than the former. The borrowing constraint operates through a loan-to-value (of collateral) ratio based on the assumption that, in the event of a loan failure, only part of the loan is recouped. It is also usually assumed that the maximum possible amount is borrowed.^[5] Consequently, as the price of the collateral asset rises, greater quantities of credit can be raised. Iacoviello (2005) estimates a model based on these ideas. The loan-to-value ratio need not be fixed (although it is in many models, such as Iacoviello (2005)) and could be allowed to vary in a stochastic way, as in Gerali et al (2010). However, ideally this would be endogenous, which requires a description of how the ratio would be set by a lending institution. Gerali et al (2010) extend the Iacoviello (2005) model to include an explicit FI sector, which allows different interest rates to different agents and exogenous shocks to bank capital. Introducing into these models shocks originating in the financial sector seems to be an important extension.

Two other ways of modelling the supply of credit by FIs should be mentioned. Gertler and Kiyotaki (2010) have many financial intermediaries which are aggregated. This serves to provide both a retail market for funds and a wholesale (inter-bank) market. Because one can observe data on the inter-bank market such extensions in the future may be helpful for empirical work. Another important feature that might need to be captured in models was pointed out by Greenlaw et al (2008). They effectively observed that the credit supplied by financial institutions would likely vary with the value at risk (VaR) of their portfolio, as that has become the standard method of determining the limit on the amount of loans that can be supplied. Because the VaR is based on the probability of returns being less than a given value this will rise in a recession, and so the ‘credit multiplier’ would be smaller.

Footnotes

This can be derived from a costly state verification problem between the lender and borrower; see, for example, Bernanke et al (1999). [1]

Using the sample 1947:Q1–2009:Q4. Data is from the Bureau of Economic Analysis ‘National Income and Product Account’ tables 1.1.6 and 1.1.6B–D. [2]

It should be noted that Leamer considerably transformed the data before reaching his conclusion. This included smoothing the residential investment data, which eliminates some of its peaks and troughs and probably made it more closely resemble those of GDP, and eliminating the difference in the growth rates of the two series. The latter has a very strong effect as the average growth rate is a key determinant of cycle characteristics – see Harding and Pagan (2002). [3]

Their core model is not strictly the Smets and Wouters one, but the principles underlying it are the same. [4]

This is done to allow log-linearisation of the model. [5]