RDP 2011-04: Assessing Some Models of the Impact of Financial Stress upon Business Cycles 7. Correspondence of Iacoviello Model Growth Cycle Outcomes with Stylised Facts
December 2011
- Download the Paper 265KB
The ‘stylised facts’ used earlier pertain to the business cycle, and it is unclear what implications these would have for detrended output, namely the growth cycle, which is output in the Iacoviello model. Furthermore, there is no external finance premium in Iacoviello's model, making it hard to define a crisis.
Here we consider whether the collateral asset prices 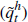 are a long way below their steady state levels, that is, the extent to which
are a long way below their steady state levels, that is, the extent to which 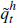 is negative. Just as before there was a question of timing, in that one might wish
to use lags of
is negative. Just as before there was a question of timing, in that one might wish
to use lags of 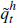 ,
so we experimented with
,
so we experimented with 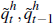 and
and 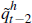 . The last seemed to give the
best results. Thus we computed
. The last seemed to give the
best results. Thus we computed 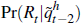 . Somewhat surprisingly we found that, when
the price of collateral was
10 per cent below steady state, the probability of a recession was 0.06,
while if it was just 10 per cent above the probability was 0.94. So high values
of the collateral price significantly raised the recession probability. This
seems an extraordinarily sensitive reaction to the collateral price. To check
the results we regressed simulated Rt against
. Somewhat surprisingly we found that, when
the price of collateral was
10 per cent below steady state, the probability of a recession was 0.06,
while if it was just 10 per cent above the probability was 0.94. So high values
of the collateral price significantly raised the recession probability. This
seems an extraordinarily sensitive reaction to the collateral price. To check
the results we regressed simulated Rt against 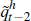 and got the linear model 0.50
+ 0.06
and got the linear model 0.50
+ 0.06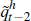 which matches the Probit results well. A non-parametric fit produced the same outcome.
It might be noted that the unconditional probability of a recession is 0.5,
as the growth cycle from the model is virtually symmetric.
which matches the Probit results well. A non-parametric fit produced the same outcome.
It might be noted that the unconditional probability of a recession is 0.5,
as the growth cycle from the model is virtually symmetric.
The feature noted in connection with the GOZ model about the importance of current shocks is again echoed here. Durations of growth cycle expansions and contractions are little changed, while the amplitudes are now 63 per cent of what they were when all shocks are included, that is, there is much less volatility.
Another feature of the Iacoviello model that is of interest is to examine what it tells us about the impact of variations in the loan-to-value ratios. One might think of this as an index of how easy it is to get credit. In the Iacoviello model the two loan-to-value ratios are set at 0.89 (entrepreneurs) and 0.55 (households), so we multiply these with a constant k in order to emulate a range of credit conditions. The values of k chosen are 0.1, 0.5, 0.9, 1.0 and 1.1, so that the fourth of these values uses the ratios in Iacoviello's (2005) work. Table 5 shows how the amplitudes of expansions and contractions for the growth cycle change for different values of k (the absolute amplitudes are virtually identical for a given k so we only present one, and the changes in the durations are relatively small). It could be regarded as surprising that easier credit leads to greater amplitudes because in the model it might have been expected to enable agents (such as impatient consumers) to better smooth their consumption, producing expenditures that are less volatile. Moreover, even very tough credit conditions (k = 0.1) lead to an amplitude that is much the same as when k = 0.5. Thus, easier credit results in a much more volatile economy, and it is apparent that, as the loan-to-value ratio approaches unity, volatility goes up a great deal. In a sense this is a story about imbalances. Keeping strong credit standards may be key to ensuring stability.
| k | Amplitude |
|---|---|
| 0.1 | 2.4 |
| 0.5 | 2.4 |
| 0.9 | 3.3 |
| 1.0 | 4.5 |
| 1.1 | 9.5 |