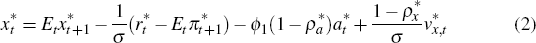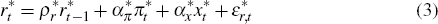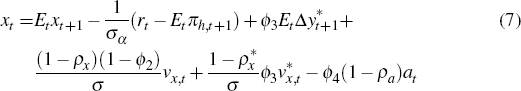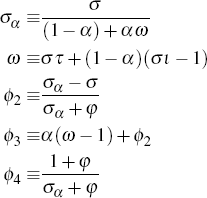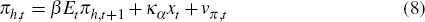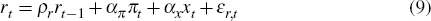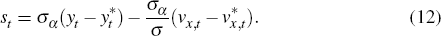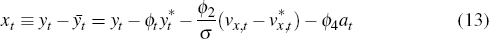RDP 2010-07: Monetary Policy and the Exchange Rate: Evaluation of VAR Models 2. A Small Open Economy DSGE Model

This section presents the small open economy DSGE model. The model is based on a modified version of that proposed by Galí and Monacelli (2005) and is described in Jääskelä and Kulish (2010). All variables are expressed in log deviations from steady state and the key log-linear equations are given below.

2.1 The Large Economy

Variables with a star superscript correspond to the large, foreign economy, which can be described with a standard set of new Keynesian closed economy equations.

Firms operate under monopolistic competition in the goods market and Calvo-price stickiness. Factor markets are competitive and goods are produced with a constant returns to scale technology. The Phillips curve in the large economy is of the form:

where: 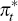is the foreign inflation rate; 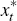is the foreign output gap; the parameter κ is strictly positive and captures the degree of price rigidities; the household's discount factor, β, lies between zero and one; and E_t denotes expectations conditional on information at time t.

The IS-curve implies that the current level of the foreign output gap depends on its expected future level 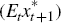, the ex-ante short-term real interest rate, foreign total factor productivity 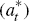and a foreign aggregate demand disturbance 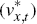, as follows:

where: 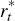is the foreign nominal short-term interest rate; σ is strictly positive and governs intertemporal substitution; 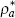is the persistence of 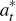; 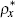is the persistence of 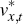; and ϕ₁ is equal to 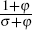, with φ > 0 governing the elasticity of labour supply.

Foreign monetary policy follows a Taylor rule of the form:

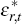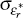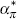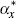where is an independent and identically distributed (iid) foreign monetary policy shock, with zero mean and standard deviation . and capture the reaction of the foreign interest rate to the deviation of foreign inflation from target (set to zero) and the foreign output gap.

The potential level of foreign output, 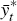, is the level that would prevail in the absence of nominal rigidities. For the large economy, it can be shown that the actual level of output, 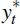, and the output gap, 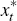, obey the following relationship:

Foreign exogenous processes evolve according to:

where: the shocks 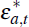and 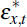are iid with zero mean and standard deviations 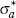and 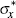, respectively; and the autoregressive parameters, 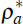and 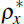are less than unity in absolute value.

2.2 The Small Open Economy

In the small open economy, the IS-curve links the output gap, x_t, to its expected future value, the ex-ante real interest rate (where the nominal interest rate is deflated by the expected rate of domestically produced goods inflation), the expected growth rate of foreign output, foreign and domestic aggregate demand shocks and domestic total factor productivity. The open economy's IS-curve takes the following form:

where: ρ_x and ρ_a are the persistence parameters of domestic aggregate demand and domestic productivity shocks, respectively; and the parameters σ_a, ϕ₂, ϕ₃ and ϕ₄ are functions of deep parameters. In particular, it can be shown that:

where: α ∈ [0, 1] captures the degree of openness; τ is the intertemporal elasticity of substitution between foreign- and domestically produced goods; and ι is the elasticity of substitution across varieties of foreign-produced goods.

The dynamics of domestically produced goods inflation, π_h,t, are governed by a Phillips curve equation:

where: κ_α ≡ λ(σ_α + φ); λ ≡ 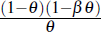; θ governs the degree of price stickiness; and v_π,t is a cost-push shock.

Monetary policy in the small economy is assumed to follow a Taylor rule that sets the nominal interest rate, r_t, in response to its own lagged value, the deviation of consumer price inflation, π_t, from its target (set to zero) and the output gap, x_t, as follows:

where ε_r,t is an iid monetary policy shock with zero mean and standard deviation σ_r.

The terms of trade, s_t, are defined as the price of foreign goods (p_f,t) in terms of the price of home goods (p_h,t). That is, s_t = p_f,t – p_h,t. The consumer price index is a weighted average of the price of foreign- and domestically produced goods p_t = (1 − α) p_h,t + αp_f,t. It follows that consumer price inflation and domestically produced goods inflation are linked by the expression:

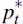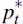The nominal exchange rate, e_t, is defined as the price of foreign currency in terms of the domestic currency, so positive values of Δ_et indicate a nominal depreciation of the domestic currency. The law of one price is assumed to hold, so p_f,t = e_t + , which implies that the terms of trade can also be written as s_t = e_t + − p_h,t. Combining these expressions, it is easy to show that the real exchange rate, q_t, is proportional to the terms of trade:

Complete international securities markets, together with the market clearing conditions, lead to the following relationship between the terms of trade, output and shocks to demand:

The relationship between the actual level of output, y_t, and the output gap, x_t, satisfies the following equation:

Finally, the domestic exogenous processes evolve according to:

where: the shocks ε_a,t, ε_π,t, and ε_x,t are iid with zero mean and standard deviations σ_a, σ_π, and σ_x, respectively; and the autoregressive parameters, ρ_a, ρ_π and ρ_x are less than unity in absolute value.