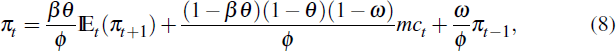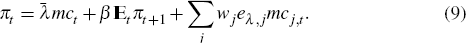RDP 2010-01: Reconciling Microeconomic and Macroeconomic Estimates of Price Stickiness 4. Estimating the Aggregate NKPC via GMM
March 2010
- Download the Paper 462KB
In this section, we examine the implications of estimating aggregate NKPCs when the true data-generating process contains either heterogeneity, roundabout production or both. These Phillips curves are estimated using GMM, following the approach of Galí and Gertler (1999).
4.1 Quantifying the Inconsistency in GMM Estimates of the NKPC
In order to quantify the effect of heterogeneity and roundabout production on estimates of the aggregate NKPC, we use a Monte Carlo approach. We generate 1,000 datasets, each with 1,000 periods, from each of the four models of Section 3, and then use GMM to estimate a single NKPC with these data. We use 1,000 periods to focus on the asymptotic properties of the estimator; results for 120-period data are qualitatively similar.
GMM is widely used to estimate the NKPC because it is able to deal with the presence of expected inflation. Inflation can be decomposed into expected inflation, IEtπt+1, which is not observed, and the forecast error, vt+1: πt+1 = IEtπt+1 + vt+1. The assumption of rational expectations is that people use all available information at time t when forming their expectations. This implies that the forecast errors should be unbiased (IEtvt+1 = 0) and uncorrelated with all time t information, so that IEt(vt+1zt) = 0, where zt is an instrument (information which was available at time t). As this should hold across time, the unconditional expectation, IE(vt+1zt) = 0, is the orthogonality (moment) condition used by GMM.
Following Galí and Gertler (1999), we also instrument for marginal costs, which they motivate as an attempt to deal with the measurement error which is likely to exist in their variables representing real marginal costs. However, it is also likely that real marginal costs are endogenous, particularly in models that incorporate roundabout production. This effectively restricts our instruments, which are described below, to be dated t − 1 or earlier.
We estimate the NKPC in its hybrid form where a fraction of firms who are able to change their prices in any given period do so mechanically by indexing to past inflation.[10] This allows us to determine whether estimates imply a role for indexation, even when none exists. Explicitly, this hybrid NKPC is of the form:
where: ω is the share of firms that index their prices; ø = θ + ω[1 – θ(1 – β)]; and mct is real marginal cost.
The exercise performed here is different to that presented in Imbs et al (2007). They simulate data from separate two-equation models for each of the sectors and estimates the reduced form aggregate NKPC via Maximum Likelihood.[11] Instead, we simulate data from a macroeconomic model with microeconomic foundations with interdependent sectors, which allows us to analyse the importance of the different sources of heterogeneity for the parameter estimates.
Galí and Gertler (1999) use the labour share of income as a measure for real marginal costs. They also use a large instrument set, including lags of inflation, real marginal costs, nominal wages growth, interest rates and detrended output. In contrast, we use a smaller instrument set for our baseline and roundabout models, as the New-Keynesian model without heterogeneity (and calibrated as described above) generates very high correlations amongst some of the potential instruments. (An alternative approach would be to incorporate more shocks into the model.) In the heterogeneous and full models we are able to use a larger instrument set, similar to Galí and Gertler (1999), as the introduction of heterogeneity considerably reduces the degree of correlation between the potential instruments. In particular, heterogeneity in factor shares and technology shocks across the sectors reduces the absolute correlation between the aggregate labour share and inflation.
The estimates based on our simulated data are presented in Table 6 and graphically using kernel density estimates in the figures that follow. The restricted instrument set includes 4 lags of inflation, growth in value added and the cash rate. The full instrument set also includes 2 lags of the labour share and wage inflation. We use a two-step GMM estimator, with a 12-lag Newey West heteroskedasticity and autocorrelation-consistent estimate of the covariance matrix, akin to Galí and Gertler (1999). We constrain the parameters β, θmacro and ω to be between 0 and 1, so as to be economically meaningful. As GMM is sensitive to the parameterisation used in the moment conditions, we report estimates using two different parameterisations (as described in the notes to Table 6).
| Models | |||||
|---|---|---|---|---|---|
| Parameter | True | Baseline | Roundabout | Heterogeneous | Full |
| Parameterisation 1 | |||||
| β | 0.99 | 1.00 (0.15) | 1.00 (0.07) | 1.00 (0.11) | 1.00 (0.01) |
| θmacro | 0.30 | 0.38 (0.18) | 0.42 (0.21) | 0.81 (0.07) | 0.85 (0.04) |
| ω | 0.00 | 0.02 (0.04) | 0.08 (0.10) | 0.09 (0.05) | 0.26 (0.05) |
| with β = 0.99 imposed | |||||
| θmacro | 0.30 | 0.47 (0.28) | 0.42 (0.19) | 0.81 (0.09) | 0.83 (0.04) |
| ω | 0.00 | 0.05 (0.04) | 0.08 (0.09) | 0.09 (0.05) | 0.24 (0.06) |
| Parameterisation 2 | |||||
| β | 0.99 | 0.73 (0.14) | 0.82 (0.10) | 1.00 (0.06) | 1.00 (0.01) |
| θmacro | 0.30 | 0.26 (0.03) | 0.27 (0.02) | 0.73 (0.04) | 0.79 (0.03) |
| ω | 0.00 | 0.00 (0.00) | 0.00 (0.01) | 0.03 (0.03) | 0.19 (0.05) |
| with β = 0.99 imposed | |||||
| θmacro | 0.30 | 0.24 (0.05) | 0.29 (0.03) | 0.72 (0.04) | 0.77 (0.03) |
| ω | 0.00 | 0.00 (0.01) | 0.00 (0.01) | 0.03 (0.03) | 0.17 (0.05) |
Notes: The median estimate is presented for each model and the estimates
in parentheses are the standard deviations of the distribution of the parameters.
The results in the lower panel of each half of the table are estimated
with the restriction that β = 0.99. The moment conditions
used to estimate the parameters are specified using two parameterisations: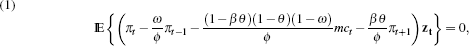 where ø = θ + ω[1 − θ(1 − β)] and zt is the vector of instruments. 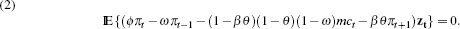 |
|||||
The estimates of the discount factor, β, are imprecise, except for the full model, where they are approximately one for both parameterisations. The results for the other parameters, however, are generally little changed if we constrain β to be its true value (0.99) (Table 6).
A common criticism of NKPCs is the need to include indexation in an ad hoc manner in order to capture the persistence of inflation evident in the data. Estimates of the NKPC based on data from the full model using either parameterisation falsely suggest that around 20 per cent of firms index their prices even though this is not a feature of the data-generating process (Table 6). These incorrect estimates of the level of indexation seems to come about through the interaction of heterogeneity and roundabout production as they are far larger in the full model than in the other models.
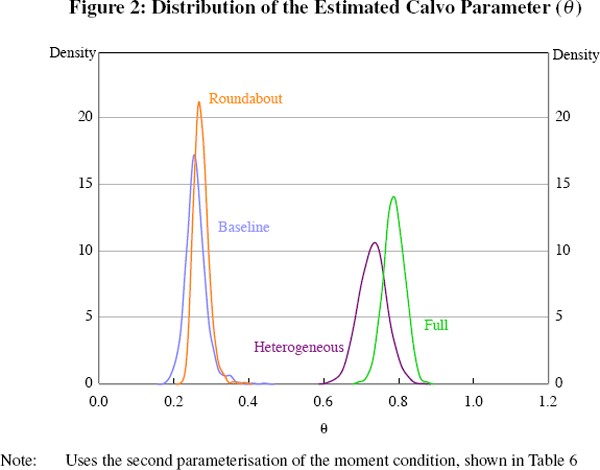
The difference between the theoretically true macroeconomic value for the Calvo probability and the estimates of the macroeconomic Calvo probability from the heterogeneous (full and heterogeneous) models is striking (Figure 2). Based on the theory presented in Section 2, the estimates of the macroeconomic Calvo probability should be about 0.30. The estimates from the heterogeneous models using either parameterisation are not even remotely close, with the median estimates for the full model being 0.85 and 0.79 respectively. Failing to account for the effect of heterogeneity on the estimates, as is commonly done, may lead one to falsely overstate the true extent of nominal rigidities. The fact that the estimated macroeconomic Calvo probability in both heterogeneous models is larger than the ‘true’ NKPC based Calvo probability, whereas theoretically we would expect it to be less, suggests a large econometric bias. Possible sources of this bias include the misweighting of marginal costs and using unsuitable instruments.
4.2 Implications of Misweighting Marginal Costs
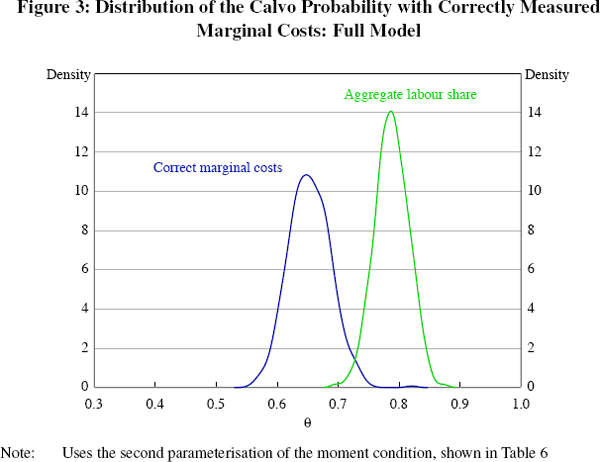
A common measure of real marginal costs used in the literature is the aggregate labour share of income (or revenue) (see, for example, Galí and Gertler 1999; Sbordone 2002). In the baseline model this is consistent with theory. However, this is not true when both roundabout production and heterogeneity are present. Instead, one should use a gross revenue-weighted average of sectoral real marginal costs, reflecting the weighting used in the construction of the aggregate price index. Using the (misweighted) aggregate labour share of income results in inconsistent estimates of the Calvo probability. The extent of this inconsistency can be gauged by comparing these ‘misweighted’ estimates to those obtained by repeating the Monte Carlo exercise with the correctly weighted series (Figure 3). It is apparent that the misweighting, while important, is not a major factor in the overestimation of the Calvo probability; the median estimate using the second parameterisation falls from 0.79 to around 0.65, still well above 0.3 (Table 7). Interestingly, the misweighting does appear to be an important source of the erroneous finding of indexation of prices in the full model; if the correct marginal costs series is used with the second parameterisation the indexation parameter more than halves in size and is no longer significantly different from zero.[12]
| Measure of marginal costs used | |||
|---|---|---|---|
| Parameter | True | Labour share | Correctly weighted |
| β | 0.99 | 1.00 (0.01) | 0.96 (0.06) |
| θmacro | 0.30 | 0.79 (0.03) | 0.65 (0.03) |
| ω | 0.00 | 0.19 (0.05) | 0.07 (0.05) |
| Imposing β = 0.99 | |||
| θmacro | 0.30 | 0.77 (0.03) | 0.66 (0.04) |
| ω | 0.00 | 0.17 (0.05) | 0.08 (0.05) |
| Notes: The median estimate is presented for each model and the estimates in parentheses are the standard deviations of the distribution of the parameters. The results in the lower panel of the table are estimated with the restriction that β = 0.99. Uses the second parameterisation of the moment condition, shown in Table 6. | |||
4.3 Lack of Suitable Instruments
Another possible source of the inconsistent parameter estimates is that the NKPC may only be weakly identified because the instruments used for future inflation and marginal costs are weak. Mavroeidis (2005) argues that this is the case for the instruments which are commonly used in the estimation of the NKPC. The results in Table 6 and Figure 2 suggest that for the baseline and roundabout models weak instruments are not a large problem. In the models with heterogeneity, it appears that weak instruments may be a problem; this problem is compounded by the fact that the instruments might not only be weak, but also invalid.
As described in Section 2 (Equation (5)), the aggregate NKPC can be expressed as a weighted sum of sectoral NKPCs (ignoring indexation):
This demonstrates that the presence of heterogeneity introduces an ‘error’
term,
Σjwjeλ,jmcjt.[13] As discussed
above, we can decompose inflation into expected inflation and the forecast
error, πt+1 = Et(πt+1)
+ νt+1. Combining these we can define a broader
error term, ut, which includes both the forecast error,
vt+1, and the error induced by heterogeneity,
that is 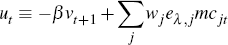 .
ut is the error term which is relevant for
estimation.[14]
.
ut is the error term which is relevant for
estimation.[14]
Recall that, given rational expectations, our GMM estimation approach assumes that
which implies that the errors are uncorrelated with the instruments, zt.
We also need the instruments to be correlated with the variables for which we are instrumenting. Therefore, we need instruments that are uncorrelated with the weighted sectoral marginal costs but are correlated with aggregate marginal costs. Among the variables available in our model, it is difficult to conceive of instruments which can satisfy this condition.[15] This problem is an example of the aggregation bias first noted by Pesaran and Smith (1995) and applied specifically to aggregate NKPCs by Imbs et al (2007).
The lack of valid instruments depends on the existence of heterogeneity in the Calvo
probabilities. If the Calvo probabilities were the same across sectors, the
coefficients on marginal costs would be constant (λj =  , and eλ,j
= 0 for all j). Therefore, the second component of ut
would disappear; it would only be comprised of the expectation error, as is
normally assumed. Consistent with this, the estimates of the Calvo probability
for the baseline and roundabout models are broadly around their true values
(Table 6 and Figure 2); it is when heterogeneity is introduced that the
estimates are upwardly biased. Also, note that if the eλ,j
and mcjt were independent then it would be possible to
express the moment condition as
, and eλ,j
= 0 for all j). Therefore, the second component of ut
would disappear; it would only be comprised of the expectation error, as is
normally assumed. Consistent with this, the estimates of the Calvo probability
for the baseline and roundabout models are broadly around their true values
(Table 6 and Figure 2); it is when heterogeneity is introduced that the
estimates are upwardly biased. Also, note that if the eλ,j
and mcjt were independent then it would be possible to
express the moment condition as 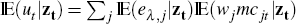 = 0, which would be satisfied if
= 0, which would be satisfied if 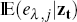 = 0. However, the distributions
of the slopes of the sectoral Phillips curves and marginal costs are not independent;
both depend on the distribution of the Calvo probabilities.
= 0. However, the distributions
of the slopes of the sectoral Phillips curves and marginal costs are not independent;
both depend on the distribution of the Calvo probabilities.
In models with heterogeneity, developments in one sector can affect other sectors and the size of the effects will depend on the distribution of the Calvo probabilities. Without roundabout production, sectors affect each other through the effect of their pricing decisions on consumer demand for other goods and the effect of their demand for labour on wages, and therefore the marginal costs faced by firms in other sectors. This is the reason why the distribution of the Calvo probabilities can matter. As an example, suppose there is a relatively large sector with flexible prices. A positive productivity shock in that sector would enable its prices to fall while its demand for labour would rise. At the same time, demand for output from other sectors would fall (as consumers buy relatively more of the now cheaper goods) and so they will reduce their labour demand. With a relatively large flexible price sector, the net effect on wages can be positive, resulting in higher marginal costs for other sectors. If the flexible price sector was relatively small, the net effect might be lower wages and lower marginal costs for other sectors. With roundabout technology, there is an additional direct effect on other firms since the prices charged by one sector will affect marginal costs in other sectors.
Note that this aggregation bias applies to any other estimation methods used to estimate aggregate NKPCs that ignore heterogeneity. For instance, Lindé (2005) uses a Full Information Maximum Likelihood approach to account for expected inflation. However, since the aggregate NKPC implicitly includes an error term that is likely to be correlated with aggregate marginal costs, estimates from this approach will also tend to be biased. Unless the estimation procedure corrects for the correlation between the regressors and the unobserved error, which is difficult as quality sector-level data are rarely available, the estimates of the NKPC remain likely to be biased.
In summary, it appears that the inconsistency that plagues estimates of the coefficient on marginal costs in the aggregate NKPC when heterogeneity is present primarily reflects model misspecification. There are two aspects to this. First, incorrect weighting affects the standard measure of marginal costs (the labour share of income) and, second, the instruments may be weak or not valid.
4.4 Sensitivity Analysis
To assess the robustness of our results we vary a number of parameters of the model and repeat the exercises performed above for the full model. First, we eliminate sector specific shocks completely. In this case, sectoral marginal costs remain heterogeneous as factor shares differ across sectors. Second, we reduce the heterogeneity in the Calvo probability by moving each sector roughly 0.1 closer to the average while maintaining the overall mean. Third, we lower the overall level of price stickiness by reducing each sector's Calvo probability, where possible, by 0.1. Finally, we estimate the purely forward-looking NKPC instead of the hybrid NKPC. The results in Table 8 show that the overstatement of price stickiness in estimates of the aggregate NKPC is robust to these alternative choices of parameters.
| Parameter |
True |
No sector-specific shocks | Less Calvo heterogeneity | Less price stickiness | Forward-looking NKPC |
|---|---|---|---|---|---|
| β | 0.99 | 0.93 (0.05) | 1.00 (0.05) | 1.00 (0.04) | 1.00 (0.00) |
| θ | 0.30 | 0.64 (0.04) | 0.79 (0.03) | 0.77 (0.03) | 0.77 (0.02) |
| ω | 0.00 | 0.05 (0.05) | 0.31 (0.05) | 0.19 (0.05) | – |
| Notes: The median estimate is presented for each model and the brackets denote the standard deviation of the estimates. Uses the second parameterisation of the moment condition. | |||||
Footnotes
This form of the hybrid NKPC is due to Galí and Gertler (1999), and is more flexible than the form in Christiano, Eichenbaum and Evans (2005) as the model is free to reject the presence of indexation. [10]
The two-equation model consists of the NKPC and an AR(2) process for marginal costs. [11]
Alternatively, with the first parameterisation the magnitude of the indexation parameter is reduced by around one-third, but remains significantly different from zero. [12]
For the models in this paper, the weights are each sector's share of gross revenue. [13]
As we allow for indexation and estimate the hybrid NKPC, 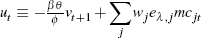 ,
where ø = θ + ω[1 – θ(1
– β)], as before.
[14]
,
where ø = θ + ω[1 – θ(1
– β)], as before.
[14]
Dees et al (2009) use a VAR to generate global or foreign instruments that may, in principle, be correlated to aggregate marginal costs and exogenous with respect to sectoral marginal costs. [15]