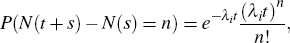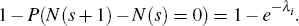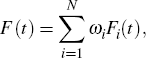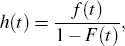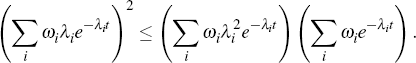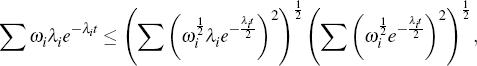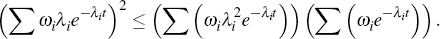RDP 2010-01: Reconciling Microeconomic and Macroeconomic Estimates of Price Stickiness Appendix B: Heterogeneous Calvo Probabilities and the Hazard Function

Appendix B: Heterogeneous Calvo Probabilities and the Hazard Function

Suppose we have an economy with N goods. The prices for each of the N goods evolve according to the Calvo mechanism. This means that the number of price changes in a given time interval follows a Poisson process. We assume that each item's price is changed at different rates. Good i's price is changed at Poisson rate λ_i so that

where N(t + s) – N(s) represents the number of events on the interval (s, s+t]. The probability of at least one price change in each period (say t = 1) is given by

The duration of prices follows an exponential distribution and so the hazard function for the duration of good i's price should be flat.

Denote the cumulative distribution function (CDF) for the time between price changes for each good by F_i(t). Now if we collect the duration of prices for each of the N goods and pool these times, the CDF of this pooled population becomes:

where ∑_iω_i = 1 and ω_i > 0 ∀i. ω_i could be set to some weight according to the relative sample sizes for each good or the weight of the good in the CPI, but we remain agnostic as to where they come from.

The hazard function is defined as the probability of a change at t divided by the survival probability

where .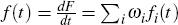

We know that 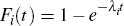, so

If λ = λ ∀i, then 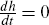. This means that if the prices of all goods in an economy are changed at the same rate, the hazard function should be flat.

If not, then the hazard function is downward-sloping.

To determine the slope of the hazard function, we only need to sign the numerator of its derivative (the denominator is always positive).

So the hazard function is downward-sloping if

Now, the Cauchy-Schwartz inequality states that

Since the terms we are dealing with are all positive, we can ignore the absolute value delimiters. If we set

we obtain:

or

In other words, the hazard function for a pooled sample should be downward-sloping.