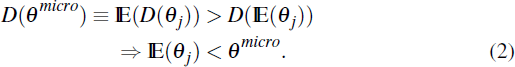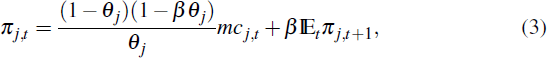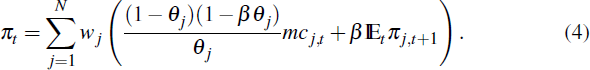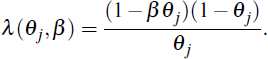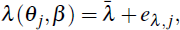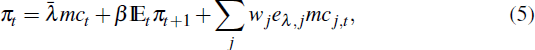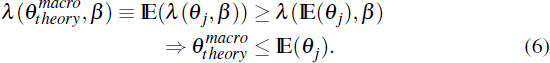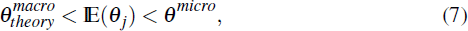RDP 2010-01: Reconciling Microeconomic and Macroeconomic Estimates of Price Stickiness 2. Comparisons of Economy-wide Calvo Probabilities
March 2010
- Download the Paper 462KB
Macroeconomic estimates of price stickiness typically rely on the assumption that all firms have the opportunity to reset their prices with the same probability. We relax this assumption and show that, at least in theory, the macroeconomic estimate of aggregate price stickiness should be less than the microeconomic-based estimate. In practice, the opposite is found – NKPC-based estimates tend to imply much more price stickiness than microeconomic-based estimates.
Under the Calvo pricing mechanism, a firm faces a probability θj (the Calvo probability) that it will not be given the opportunity to re-optimise the price it charges for its output in a given period. For such a firm, the output price would have an average duration given by
which is a strictly increasing and convex function in the Calvo probability, θj. Since D(θ) is non-linear, we show below that inferring an economy-wide Calvo probability from an economy-wide average duration will yield an estimate which differs from that which is relevant for determining the slope of the aggregate NKPC. The discrepancy between these two Calvo probabilities turns out to be economically significant, as they imply substantially different degrees of aggregate price stickiness.
2.1 Microeconomic-based Estimates
Microeconomic-based studies typically calculate the average length of time that prices are fixed for a particular product j, and compute a weighted average of these average durations to produce an economy-wide estimate for the average duration of prices, denoted by IE(D(θj)) (see, for example, Klenow and Kryvtsov 2008; Nakamura and Steinsson 2008). Some economists then infer a Calvo probability, θmicro, from this statistic. If the Calvo probability were homogenous across firms, θmicro would reflect the economy-wide average Calvo probability, denoted by IE(θj). However, given the non-linearity of Equation (1) described above, Jensen's inequality tells us that when firms face different Calvo probabilities, θmicro will be greater than the average Calvo probability IE(θj), that is
IE(θj) and θmicro are equal only in the absence of heterogeneity.
2.2 Macroeconomic-based Estimates
Using a similar argument, we can compare macroeconomic-based estimates of the Calvo probability inferred from an aggregate NKPC to the average Calvo probability from microeconomic data.
Assume that there are a finite number of sectors in the economy with firms in any given sector facing the same Calvo probability, but with Calvo probabilities varying across sectors. Each sector j, with Calvo probability θj, would therefore have its own NKPC given by
where: πj,t is inflation in sector j; β is the subjective discount factor of households; and mcj,t is the real marginal cost faced by firms in sector j. A NKPC for aggregate inflation, πt, is obtained by weighting each sectoral NKPC according its weight in the price index (wj)
Let the coefficient on marginal costs for a particular sector's NKPC be denoted as
We can decompose the coefficient on marginal costs as follows,
where 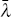 is a weighted average of the coefficients on marginal costs across the sectors;
and eλ, j is the deviation from this average for
a particular sector. We can then write the aggregate NKPC as
is a weighted average of the coefficients on marginal costs across the sectors;
and eλ, j is the deviation from this average for
a particular sector. We can then write the aggregate NKPC as
where: 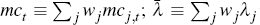 ;
and the last term can be thought of as an ‘error’ term. Assuming
that we can estimate
;
and the last term can be thought of as an ‘error’ term. Assuming
that we can estimate 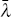 without bias, and taking β
as given, we can infer the macroeconomic estimate of the Calvo probability,
without bias, and taking β
as given, we can infer the macroeconomic estimate of the Calvo probability,
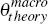 ,
which solves
,
which solves 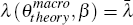 . Since λ(θ,
β) is decreasing and convex in θ, we obtain
. Since λ(θ,
β) is decreasing and convex in θ, we obtain
2.3 Comparing Microeconomic and Macroeconomic Estimates
From Equations (2) and (6) we have
with equality holding if all firms face the same Calvo probability. Therefore, macroeconomic
estimates of the Calvo probability should be lower than corresponding microeconomic
estimates. However, the evidence we cited in the introduction goes in the opposite
direction; in practice, macroeconomic estimates of the Calvo probability 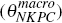 are typically much larger than microeconomic estimates (θmicro).
are typically much larger than microeconomic estimates (θmicro).
Part of the tension between the microeconomic and macroeconomic estimates of the Calvo probability reflect how θmicro itself is constructed. A better way to utilise the microeconomic data in order to produce an estimate of the Calvo probability is to separately derive Calvo probabilities for each sector from the duration of that sector and then weight these appropriately. This is IE(θj).
However, IE(θj) is not the relevant estimate for the purpose
of determining the slope of an aggregate NKPC. This is 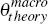 , which can be derived
from the weighted average of the coefficients on marginal costs in the sectoral
NKPCs.
, which can be derived
from the weighted average of the coefficients on marginal costs in the sectoral
NKPCs.
Given the results from a pricing survey undertaken by the Reserve Bank of Australia
presented later in Table 1 (Section 3.2), the Calvo probability
consistent with this approach is 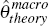 = 0.30, implying that prices are fixed for
just over 4 months on average, whereas the commonly used Calvo probability
from the average duration statistic is
= 0.30, implying that prices are fixed for
just over 4 months on average, whereas the commonly used Calvo probability
from the average duration statistic is 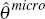 = 0.59, suggesting
prices are fixed for just over 7 months on average, and IE(θj)
= 0.48. These are all much smaller than the estimate of
= 0.59, suggesting
prices are fixed for just over 7 months on average, and IE(θj)
= 0.48. These are all much smaller than the estimate of 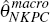 = 0.94 from the NKPC
for Australian data in Kuttner and Robinson (forthcoming).
= 0.94 from the NKPC
for Australian data in Kuttner and Robinson (forthcoming).
| Sector | Average duration (quarters) | Calvo probability (θj) |
|---|---|---|
| Agriculture | 4 | 0.75 |
| Construction | 1⅓ | 0.25 |
| Manufacturing | 2 | 0.50 |
| Mining | 4 | 0.75 |
| Utilities | 4 | 0.75 |
| Wholesale and retail trade | 1 | <0.25 (0.1)b |
| Transport and storage | 4 | 0.75 |
| Business services | 4 | 0.75 |
| Household services | 4 | 0.75 |
| Tourism | 4 | 0.75 |
| Memo items: | ||
| IEθj | 0.48 | |
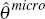 |
0.59 | |
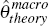 |
0.30 | |
|
Notes: (a) The Calvo probability (θj) is the probability that an intermediate-goods
firm in sector j cannot reoptimise its price in a given quarter.
Sources: RBA; authors' calculations |
||
As we will show later, estimates of price stickiness from aggregate NKPCs 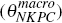 are high primarily for two reasons. First, in the presence of roundabout production
and heterogeneity in factor shares, the aggregate NKPC is misspecified when
the aggregate labour share is used as the measure of aggregate marginal costs.
Second, heterogeneity implies that commonly used instruments may be weak and
invalid, and this is exacerbated if roundabout production also exists.
are high primarily for two reasons. First, in the presence of roundabout production
and heterogeneity in factor shares, the aggregate NKPC is misspecified when
the aggregate labour share is used as the measure of aggregate marginal costs.
Second, heterogeneity implies that commonly used instruments may be weak and
invalid, and this is exacerbated if roundabout production also exists.
Note that these problems are not specific to GMM and apply to all estimates of aggregate NKPCs which fail to account for roundabout production and heterogeneity.