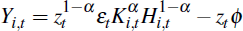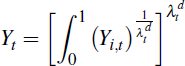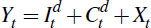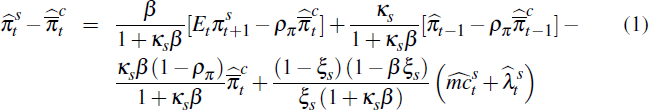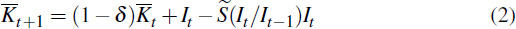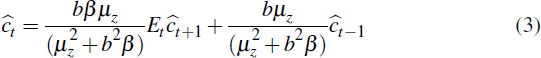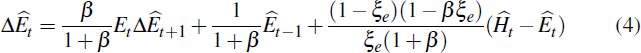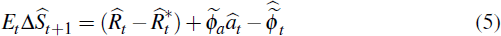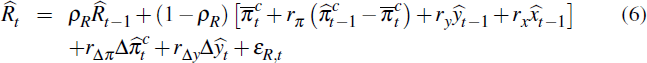RDP 2008-07: A Medium-scale Open Economy Model of Australia 2. The Model – Main Features
December 2008
- Download the Paper 485KB
The benchmark set-up of the model closely follows the open economy extension of Altig et al (2005) and Christiano, Eichenbaum and Evans (2005) by Adolfson et al (2007). For a detailed discussion of the basic model readers should refer to these sources (and Appendix B). In what follows we provide a brief sketch of the key features of the model. The model consists of a domestic economy populated with households that consume goods, supply labour and own the firms that produce the goods. Domestic households trade with the rest of the world by exporting and importing differentiated consumption and investment goods. Consumption and investment goods are also produced domestically for domestic use. There is also a firm that produces a commodity good that is exported abroad. The domestic economy is small in the sense that developments in the domestic economy are assumed to have only a negligible impact on the rest of the world.
Almost all the theory of the model can be understood in terms of households and firms responding to changes in relative prices. There are four main types of goods in the domestic economy: domestically produced and imported consumption goods and domestically produced and imported investment goods. Households will choose to consume and invest more of the type of good that is relatively cheap. The relative price between imported and domestic goods thus determines the import share in domestic consumption and investment. Similarly, the intertemporal decision to invest and consume can be understood in terms of the relative prices of goods today compared with expected future prices, which will depend on inflation. Households need to work in order to earn wages, their labour supply decision depends on the real wage offered and the marginal utility associated with the marginal increase in wage income that would come about by supplying an additional increment of labour (which leaves less time for valuable leisure).
The model has a number of frictions that slow down the alignment of relative prices and quantities to their steady-state values. All goods prices and wages are subject to Calvo-type nominal frictions. These prevent the aggregate price level from adjusting immediately to shocks. The same kind of friction is also present in households' wage-setting decisions. In addition, there are also real frictions in the model that imply that even in the absence of nominal frictions, adjustment to shocks is not instantaneous. The real frictions in the model include costs of adjusting investment and employment, and habit formation in consumption.
The structure of the model and the various frictions that determine its dynamics are outlined below in some detail.[2] However, for a more formal description of the model, we refer interested readers to Adolfson et al (2007).
2.1 Production
There is a continuum of firms, indexed by i ∈ (0,1), that produce intermediate domestic goods using the decreasing returns to scale production function
where zt is a non-stationary world productivity shock, εt is a persistent but stationary Australian-specific technology shock and Ki,t and Hi,t are capital and labour inputs at firm i, respectively. The last term, ztø is a fixed cost of production that ensures zero profits (from monopolistic competition) in steady state. It can be expressed in terms of a mark–up paid over the firm's marginal cost.
Intermediate goods are combined into the final good Yt using a constant elasticity of substitution aggregator
Total final goods produced domestically must be used for final domestically produced
investment goods 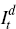 ,
consumption goods
,
consumption goods 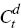 or exports Xt, thereby
satisfying the resource constraint.
or exports Xt, thereby
satisfying the resource constraint.
2.2 Nominal Frictions
There are three categories of firms operating in the economy – domestic, importing and exporting firms – which face nominal frictions that affect their price setting.[3] Similarly, domestic households face constraints on the frequency with which they can adjust the prices of the labour services they sell.
Monopolistically competitive firms produce intermediate goods using labour and capital for private consumption and investment (used to form the physical capital stock, together with imported investment goods). All types of intermediate goods are sold at a time-varying mark-up over their marginal cost. The intermediate good firms are not able to re-optimise their prices in each period, and when prices are re-optimised, they are set to maximise the discounted expected value of future profits. Since prices are not re-optimised in every period, firms need to take into account future marginal costs and mark-ups when current prices are set. Firms that are unable to re-optimise their prices in a given period index their prices to the previous period's inflation. All firms operating in the intermediate goods market solve symmetric pricing problems, though the frequency of price changes and the time-varying mark-ups are allowed to differ across types of goods.
Marginal costs also differ across different types of goods and sectors. The marginal costs of domestic producers of investment and consumption goods are determined by the cost of production, that is, wages and productivity. The marginal cost of importers depends on the exchange rate and the world price level. The marginal cost of exporters depends on the price of domestic goods they sell to the world market and the exchange rate.
Both importers and exporters are subject to price frictions stemming from assumptions regarding the currency in which the prices of exported and imported goods are set. Import prices are set in domestic currency and there is local (domestic) currency price stickiness. This captures the idea that nominal frictions are local to the market where output is sold. For instance, foreign price shocks pass through to domestic prices only gradually. However, in the long run, there is complete pass-through of changes in marginal costs of imported consumption and investment goods to the domestic economy. Export prices are set in the local currency of the export market, and prices are sticky in those currencies. This ‘pricing-to-market’ assumption, together with the sticky local currency prices, provides a short-term channel allowing for deviations from the law of one price.
2.2.1 Prices
Following much of the literature, price stickiness is introduced by making prices subject to the Calvo (1983) mechanism. The model allows for different degrees of price rigidities and indexation depending on the type of good and sector.[4] We can write a generic Phillips curve for each type of good denoted by superscript s as follows
where: 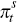 is the change in the log of the price index of good type s;
is the change in the log of the price index of good type s; 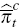 is the perceived inflation
target. Throughout the paper, a hat (ˆ) denotes log-linearised variables.
The degree of indexation is governed by the parameter κs:
if κs = 0, the Phillips curve (1) is purely forward-looking,
and if κs = 1, prices are fully indexed to last
period's inflation. β is the discount factor, ρπ
is the persistence of the inflation target (more on this below), ξs
is the Calvo probability of a firm not re-optimising the price of its good in a given
period,
is the perceived inflation
target. Throughout the paper, a hat (ˆ) denotes log-linearised variables.
The degree of indexation is governed by the parameter κs:
if κs = 0, the Phillips curve (1) is purely forward-looking,
and if κs = 1, prices are fully indexed to last
period's inflation. β is the discount factor, ρπ
is the persistence of the inflation target (more on this below), ξs
is the Calvo probability of a firm not re-optimising the price of its good in a given
period, 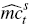 is the (log deviation of) firm's marginal
cost of producing good s and
is the (log deviation of) firm's marginal
cost of producing good s and 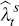 can be interpreted
as the desired mark-up of good type s.
can be interpreted
as the desired mark-up of good type s.
2.2.2 Wages
Wages exhibit stickiness and inertia due to nominal frictions built into the model. Each household supplies a differentiated type of labour to firms and therefore has some market power to determine its wage. However, households can only re-optimise their wage with probability (1 – ξw) in any given period.
Both the stickiness of nominal wages and the labour demand constraint are taken into account by households when they set their optimum wage. The fraction of households that are not able to re-optimise their wage in a given period index their wage. In doing so, they take account of the inflation target, lags of CPI inflation and wages, and the steady-state growth rate of technology.
2.3 Real Frictions
In addition to these nominal frictions, there are several sources of real frictions in the model. These frictions slow down the adjustment of quantities towards long-run steady-state values independently of the nominal frictions, and they are potentially important for the model's ability to match the data.
2.3.1 Capital adjustment costs
Firms rent capital from the households who own all domestic resources. Households can increase the economy's productive capacity by either investing in additional physical capital (which takes one period to come into the production process) or by increasing the utilisation rate of the current capital stock, thereby increasing the effective level of capital entering into production. However, adjusting the capital stock is assumed to be costly. In particular, the standard capital accumulation equation includes an extra term as in Christiano et al (2005) such that
where 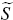 (·)
is a concave function such that marginal productivity of investment (in terms
of produced physical capital) is decreasing in the ratio of current investment
over past investment, and its minimum is at the steady state of the growth
rate of real investment. Changing the rate of capital utilisation is also
costly (see Appendix B for details).
(·)
is a concave function such that marginal productivity of investment (in terms
of produced physical capital) is decreasing in the ratio of current investment
over past investment, and its minimum is at the steady state of the growth
rate of real investment. Changing the rate of capital utilisation is also
costly (see Appendix B for details).
2.3.2 Habit formation
Household preferences are assumed to display habit persistence. So, current consumption depends on expected future consumption through the standard intertemporal consumption smoothing argument and it also depends on past consumption. The optimum consumption condition is given by the Euler equation
where the habits parameter b captures the degree of inertia in consumption.
2.3.3 Employment
Firms face an additional Calvo-like rigidity: they can adjust the level of employment to the preferred level only at random intervals (captured by the Calvo parameter, ξe). This friction creates a deviation between aggregate hours (H – actual work done) and employment (E – number of workers). The employment equation is
2.3.4 International trade in assets and the UIP condition
Households can save and lend in both domestic and world currency assets. However, financial market integration is assumed to be imperfect, as captured by two extra terms that enter the standard uncovered interest rate parity condition
where: 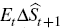 is the expected nominal depreciation of the domestic currency; and
is the expected nominal depreciation of the domestic currency; and 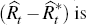 is the interest rate
differential. There are two risk premia terms,
is the interest rate
differential. There are two risk premia terms, 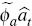 and
and 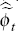 . The latter is an
exogenous risk-premium shock. The former implies that an economy will have
higher interest rates if it is a net debtor (that is, net assets,
. The latter is an
exogenous risk-premium shock. The former implies that an economy will have
higher interest rates if it is a net debtor (that is, net assets, 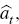 are negative), everything
else equal. This term also ensures that net debt is stationary.
are negative), everything
else equal. This term also ensures that net debt is stationary.
2.4 Central Bank
As a consequence of nominal and real frictions, changes in short-term nominal interest rates are not matched one-for-one by changes in expected inflation, leading to movements in real interest rates and creating a role for monetary policy in stabilisation.
The central bank sets the nominal interest rate 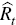 and we approximate its decision-making process with a flexible Taylor-type rule
and we approximate its decision-making process with a flexible Taylor-type rule
The nominal short rate responds to lagged interest rates 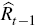 ,
deviations of lagged CPI inflation
,
deviations of lagged CPI inflation 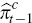 from the perceived
medium-term inflation target
from the perceived
medium-term inflation target 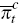 , lagged output
, lagged output 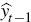 , the lagged real exchange
rate
, the lagged real exchange
rate 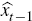 ,
and changes in inflation
,
and changes in inflation 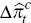 and output
and output 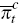 . Finally, εR,t
is an uncorrelated monetary policy shock.
. Finally, εR,t
is an uncorrelated monetary policy shock.
2.5 Government
The government is represented by a VAR(2) for taxes on capital income, labour income, consumption and payrolls. These variables are treated as exogenous in the model. After taxes are collected, they are paid back to households as a lump sum transfer. The role of taxes in the economy is thus confined to influencing marginal costs of production and marginal returns on assets.
2.6 The Foreign Economy
The foreign economy is represented by a simple VAR(4) process for trade-weighted G7 GDP (linearly detrended), inflation and a simple average of US, euro area and Japanese interest rates. These variables are also exogenous in the model.
2.7 Export Demand and the Commodities Sector
A large share of Australian exports are commodities that are traded in markets where individual countries have little market power. The standard specification of export demand is amended to reflect the fact that Australian exports and export income depend on more than just the relative cost of production in Australia and the level of world output, as would be the case in a standard open economy model. Two shocks are added to the model. The first shock, εcom,t, captures variations in exports that are unrelated to the relative cost of the exported goods and the level of world output. We also want to allow for ‘windfall’ profits due to exogenous variations in the world market price of the commodities that Australia exports. We therefore add a shock εPcom,t to the export income equation as well. It is worth emphasising here the different implication of a shock to export demand, as opposed to a shock to export income: the former leads to higher export incomes and higher labour demand, while the latter improves the trade balance without any direct effects on the demand for labour by the exporting industry.
2.8 Exogenous Shocks
In addition to these two external shocks just mentioned, there is the set of exogenous
‘domestic’ shocks in the model: the non-stationary technology
(μz,t) and stationary technology (εt)
shocks; the mark-up shocks for domestic goods 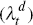 , imported consumption
goods
, imported consumption
goods 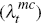 ,
imported investment goods
,
imported investment goods 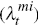 and wages
and wages 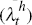 ; the consumption preference
shock
; the consumption preference
shock 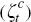 ;
the labour supply shock
;
the labour supply shock 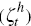 ; the investment-specific productivity shock
(ϒt); the risk premium shock
; the investment-specific productivity shock
(ϒt); the risk premium shock 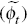 ; the monetary policy
shock (εR,t); the
medium-term (perceived) inflation target shock
; the monetary policy
shock (εR,t); the
medium-term (perceived) inflation target shock 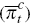 ; and the asymmetric
world productivity shock
; and the asymmetric
world productivity shock 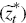 .The monetary policy and the domestic mark-up
shocks are white noise, all the other follow AR(1) processes.
.The monetary policy and the domestic mark-up
shocks are white noise, all the other follow AR(1) processes.
Footnotes
See also Appendix B, which presents the model equations in their log-linearised form. [2]
There is also a commodity exporting sector in the model. It is assumed that a single firm produces a homogenous commodity good that is exported abroad. Production evolves with the same stochastic trend as other real variables. The commodity producer is a perfectly competitive price-taker; the price and demand for commodities are determined completely exogenously in the foreign market. [3]
Firms are also assumed to face varying degrees of competition in different markets, which implies that they may receive a different profit margin from the sale of their goods in each market. [4]