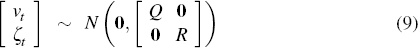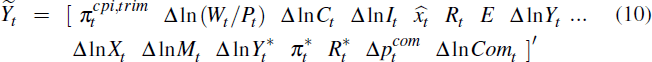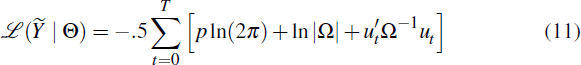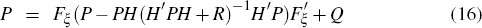RDP 2008-07: A Medium-scale Open Economy Model of Australia 3. Measurement and Estimation Strategy

The model is estimated using Bayesian methods. This section outlines our estimation strategy, including how the priors were chosen and how the variables of the theoretical model are mapped into observable time series.

3.1 Measurement

We can write the solved model in state space form

where the theoretical variables (consistent with the model) are collected in the state vector 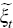and the observable variables are collected in the vector 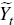. The state transition Equation (7) governs the law of motion of the state of the model and the measurement Equation (8) maps the state into observable variables. The matrices F_ξ, A_X, H′ and Q are functions of the parameters of the model and, insofar as all the structural parameters have distinct implications for the observable variables, all parameters will be identified. However, no general results exist regarding whether this will be the case, though there are ways to increase the chances of identifying a large number of parameters, for instance by making the rank of H′ as large as possible.

In our benchmark specification, we use much the same indicators as Adolfson et al (2007). The observable variables in the vector 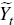are (trimmed mean) CPI inflation, the real wage, real consumption, real investment, the real exchange rate, the overnight cash rate, employment, real GDP, real exports, real imports, foreign output, foreign inflation, the foreign interest rate, commodity price inflation and commodity export volumes. That is,

The covariance matrix R of the vector of measurement errors ζ_t in Equation (8) are set to 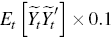so that approximately 10 per cent of the variance of the observable time series is assumed to be due to measurement errors.

3.2 Bayesian Estimation

The parameters of the model are estimated using Bayesian methods that combine prior information and information that can be extracted from the indicators in 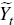. The methodology was introduced to models suitable for policy analysis by Smets and Wouters (2003). An and Schorfheide (2007) provide an overview of the main elements of Bayesian inference techniques in dynamic stochastic equilibrium models.

Conceptually, the estimation works in the following way. Denote the vector of parameters to be estimated Θ and the log of the prior probability of observing a given vector of parameters ℒ(Θ). The function ℒ(Θ) summarises what is known about the parameters prior to estimation. The log likelihood of observing the data set 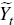for a given parameter vector Θ is denoted 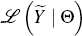. The posterior estimate 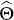of the parameter vector is then found by combining the prior information with the information in the estimation sample. In practice, this is done by numerically maximising the sum of the two over Θ, so that .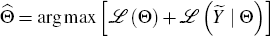

3.2.1 The priors

Our assumptions for the prior distributions of the estimated parameters closely correspond to those in Adolfson et al (2007) (see also Smets and Wouters 2003) with some exceptions: we impose simple uniform priors on the indexation parameters, the elasticities of substitution and standard deviations of the structural shocks. In the benchmark specification we impose rather tight priors on some of the policy parameters, particularly on r_x, which control the adjustment of the short-term interest rate to the real exchange rate. The priors on the parameters governing nominal stickiness, the persistence of the exogenous variables, and the parameter governing the importance of habit formation are all assigned relatively dispersed beta distributions. These priors are used to ensure that these parameters are bounded below unity.

The priors for the remaining parameters are truncated uniform, where the truncation ensures that the parameters stay in the domain prescribed by the fact that variances are positive and other bounds implied by economic theory. In Appendix C we also report the estimated distributions of the parameters imposing constant weight priors.^[5]

3.2.2 Computing the likelihood

Given the state space form, Equations (7)–(8), the likelihood for a given set of parameters can be evaluated recursively

where p is the dimension of and

is the covariance of the one-step ahead forecast errors u_t. These can be computed from the innovation representation

where K is the Kalman gain

Footnote

For more details see Chernozhukov and Hong (2003). [5]