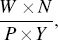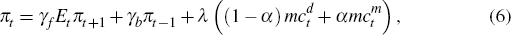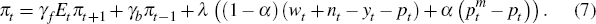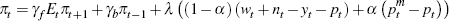RDP 2008-05: Understanding the Flattening Phillips Curve 5. Explaining the Flattening Phenomenon
October 2008
- Download the Paper 318KB
The evidence presented in Sections 2 and 4 indicates that something has changed in the way inflation responds to real marginal costs, as measured by labour's share of income. Also evident is that the relationship between the output gap (when measured as de-trended output) and labour's share of income, is far from tight. We now review the suspects which have been raised in the literature to see which (if any) can plausibly explain these observations.
The candidate explanations fall into four groups. The first is simply that there are problems with the data; that is, that the reported labour share is mismeasured in some important way. The second possibility is that the labour share is measured reasonably well – but that it is a flawed proxy for the ‘true’ marginal costs faced by firms. A third alternative explanation is that there may have, in fact, been structural changes to price-setting behaviour, and the reduction in the estimated sensitivity of inflation to costs is an accurate reflection of those changes. The fourth possibility is that the price-setting behaviour of firms has been time-invariant, but some other aspect of the model is invalid. The third and fourth possibilities suggest that the standard new-Keynesian framework that we have used here is too simple, and needs to be modified so as to better capture the inflation process.
5.1 Data Problems
At first glance, an appealing feature of the new-Keynesian framework is that it does not depend on the output gap, which is unobserved and therefore difficult to estimate, particularly in real time (see, for example, Orphanides and van Norden 2002). However, measuring marginal cost is not straightforward either. As noted above, the conventional measure of real marginal cost is labour's share of nominal output:
where: W is average compensation per-hour; N is total hours; Y is real output; and P is the price level. This is equivalent to unit labour costs – (W × N)/Y, that is, productivity-adjusted wages – deflated by the price level. In order to avoid problems associated with measuring agricultural and government output, the standard practice for the United States has been to use the labour share of income for the non-farm business sector. However, even when we constrain our attention to the non-farm business sector, considerable measurement problems may still exist, many of which are outlined in Krueger (1999). Examples of such issues include what constitutes income (for example, whether to include stock options, fringe benefits, etc), whether distinctions based on a firm being incorporated or not are useful, and whether proprietors' income should be included in returns to capital or labour. Some of these issues have the potential to not only alter the level of labour's share of income, but also to contribute to long-term trends. An example of this is the shift of proprietors to salaried employees that occurred in the United States in the first half of the 20th century (see Krueger 1999, and the references therein).
It is impossible to know for sure the extent of these data problems; however, they would have to be quite large to account for the shift in labour's share of income that has occurred in the United States.[23]
5.2 Labour Share ≠ Marginal Cost
Another logical possibility is that the labour share data are basically sound, but that the labour share is a poor proxy for firms' true marginal cost. It has long been known that the conditions under which labour's share is proportional to marginal cost are highly restrictive: sufficient conditions are that the production function is Cobb-Douglas (or more precisely, isoelastic with respect to labour), and free from complications such as labour hoarding, overhead labour, etc.[24] Rotemberg and Woodford (1999) provide a comprehensive survey of how such complications would affect the cyclicality of labour's share. What Rotemberg and Woodford do not consider, however, is the possibility of prolonged, and possibly structural, changes in labour's share of income, like that which seems to have taken place in the United States.[25]
5.2.1 Open economy dimensions
An obvious reason why labour's share may not capture marginal costs well is that it omits open-economy aspects, which are likely to be of importance, particularly for small, open economies. To examine whether there is still evidence of a structural flattening once these factors are accounted for, we estimate new-Keynesian Phillips curves for Australia.
In introducing the open-economy aspects, it is useful to distinguish between two stages of pass-through of exchange rates to consumer prices: the first being from world prices to import prices ‘at the docks’, and the second from these prices at the docks to consumer prices. Past evidence for Australia (for example, Dwyer and Leong 2001) suggests that first-stage pass-through is rapid, whereas the second stage is prolonged. Incomplete short-run pass-through has also been found for other economies – see Campa and Goldberg (2002). A simple way to introduce this in a new-Keynesian framework was developed by Monacelli (2006). In brief, he assumes that the CPI can be split into prices of domestically produced goods and prices of foreign goods. Prices of domestically produced goods evolve as sketched in Section 3.1. The law of one price is assumed to hold at the docks, that is, first-stage pass-through is complete. Incomplete short-run second-stage pass-through is captured by introducing Calvo pricing. Essentially, we obtain two Phillips curves, one each for domestically produced and foreign goods. In the latter, the measure of marginal costs are import prices at the docks relative to the retail price of foreign goods, which Monacelli (2006) terms the ‘law-of-one-price-gap’.
Such a system of Phillips curves have been estimated for Australia as part of a small DSGE model by both Nimark (2007) and Justiniano and Preston (forthcoming). In these models the retail price of foreign-produced goods is treated as an unobserved variable, and is estimated using the Kalman filter. Unfortunately, a direct measure of these prices is not available and, therefore, in order to estimate a Phillips curve using the same methods as above, we make the simplifying assumption that the Calvo parameter is the same in the domestically produced and foreign goods. This assumption is not supported by Nimark (2007) and Justiniano and Preston (forthcoming), who find that it differs across the sectors although, interestingly, Justiniano and Preston find the duration between price changes to be less for foreign goods, whereas Nimark finds the opposite.[26] The resulting aggregate Phillips curve which incorporates import prices is of the form:
where: α is the share of foreign goods in consumption; and d and m denote domestically produced goods and imports, respectively. Essentially, real marginal costs are a weighted average of marginal costs in each sector, with the weights determined by their importance in the consumption bundle.[27] Substituting in our expressions for marginal costs (and letting lower-case letters denote natural logs of variables) yields the equation we estimate:
This specification of marginal costs is strikingly similar to the long-run term in mark-up error-correction mechanism equations which have traditionally been used to model Australian inflation (for example, de Brouwer and Ericsson 1998). Interestingly, when modeling the CPI, the labour share will be an imperfect measure of real marginal costs, independent of any open economy aspects, as it deflates nominal marginal costs (unit labour costs) by the GDP deflator rather than the CPI.[28] As the weight of imported goods in consumption, α, has been a difficult parameter to estimate in the past (see Kulish and Rees 2008), we also try a variant in which it is calibrated to 0.2.[29] The results presented in Table 3 suggest that even when open economy aspects are added to the Phillips curve a flattening is evident.
| Coefficient | 1960:Q1–1992:Q4 | 1993:Q1–2007:Q2 | 1960:Q1–2007:Q2 | |||||
|---|---|---|---|---|---|---|---|---|
| Value | Standard error |
Value | Standard error |
Value | Standard error |
|||
| γb | 0.180 | 0.104 | 0.382 | 0.045 | 0.165 | 0.096 | ||
| γf | 0.777 | 0.117 | 0.596 | 0.048 | 0.804 | 0.112 | ||
| λ | 0.004 | 0.003 | 0.002 | 0.004 | 0.004 | 0.003 | ||
| α | 0.354 | 0.404 | 0.226 | 0.439 | 0.327 | 0.282 | ||
| Imposing α = 0.2 | ||||||||
| γb | 0.181 | 0.104 | 0.382 | 0.045 | 0.166 | 0.096 | ||
| γf | 0.776 | 0.118 | 0.596 | 0.047 | 0.806 | 0.111 | ||
| λ | 0.004 | 0.003 | 0.002 | 0.002 | 0.003 | 0.003 | ||
| Imposing α = 0.2 and γf + γb = 1 | ||||||||
| γb | 0.175 | 0.099 | 0.387 | 0.049 | 0.161 | 0.092 | ||
| λ | 0.002 | 0.002 | 0.001 | 0.001 | 0.002 | 0.002 | ||
| Notes: Estimated using 2SLS with Newey-West standard errors (using 12 lags). Instruments: constant, πt−1 to πt−4, lags 1–2 of the output gap, real unit labour costs, real import prices and nominal wages. | ||||||||
5.2.2 Changing sectoral composition
The observed evolution of labour's share for the United States may also reflect changes in the sectoral composition of output. McAdam and Willman (2004) show, using a disaggregated supply-side model, that shifts across sectors will affect the aggregate equilibrium mark-up, and thus labour's share. Their model includes two sources of such shifts: one is differential technical progress across sectors, which induces changes in relative prices and hence demand; the second is changes in the (exogenous) price of exports, relative to foreign goods.
Based on their model, they propose a correction to the measured labour share, which essentially is an adjustment for a time trend (capturing differentials in productivity growth) and the relative export price. They claim that this adjustment makes euro-area marginal cost stationary, and greatly improves the performance of the new-Keynesian Phillips curve. However, the results from Lawless and Whelan (2007), which estimate disaggregated inflation equations based on sectoral-level mark-ups, are less supportive of an important role for sectoral shifts in explaining the behaviour of labour's share.
5.3 Structural Changes in Price-setting Behaviour
In explaining the apparent flattening of the new-Keynesian Phillips curve, a logical possibility is that there really has been a change in underlying price-setting behaviour. A number of hypotheses fall under this rubric, and many of these are based on the idea that globalisation has fundamentally changed the economy's behaviour.
5.3.1 The Rogoff hypothesis
Perhaps the best-known of these is that of Rogoff (2003) and Rogoff (2006). His hypothesis incorporates two distinct effects: first, that globalisation has increased pricing ‘flexibility’ (that is, reduced θ, the share of firms not adjusting in any given period); and second, that increased competition has reduced product mark-ups. Rogoff argues that both of these effects will tend to increase the slope of the Phillips curve. Policy-makers, now faced with a less-favourable short-term output-inflation trade-off, will be less tempted to pursue expansionary policies in order to boost output – and this will, in turn, reduce the Barro-Gordon inflation bias.
However, as pointed out by Ball (2006), the problem with the Rogoff hypothesis is that its implication with regard to the slope of the Phillips curve is precisely the opposite of what one sees in the data: the Phillips curve has become flatter, not steeper. Moreover, the smaller equilibrium mark-up implied by the increase in competition would imply a larger labour share, and thus is inconsistent with the observed downward movement for the United States. Consequently, it seems safe to join Ball in dismissing the Rogoff hypothesis.
5.3.2 Increased openness of product and labour markets
Another globalisation-related hypothesis is that greater openness means that increases in domestic demand are increasingly satisfied through imports, rather than domestic production. This implies that increases in the output gap will have smaller effects on domestic marginal costs – and hence, muted inflationary consequences. This mechanism has been incorporated in the model developed in Razin and Binyamini (2007) and is consistent with the view expressed in Borio and Filardo (2007). A corollary is that the global output gap has become more important as a determinant of inflation. Similarly, Borio and Filardo argue that increased openness of labour markets should attenuate the inflationary effects of output fluctuations. For an overview of the channels through which globalisation may impact on the inflation process, see Bernanke (2007).
Increased openness, however, is probably insufficient to explain the flattening of the new-Keynesian Phillips curve. The reason is simple: while both developments would tend to weaken the link between the output gap and marginal costs, neither of the mechanisms above are likely to affect the link from expected future costs to inflation. In the estimates above for Australia, the share of imported goods in the consumption bundle appears to have fallen, although this is imprecisely estimated and is at odds with the increase in the share of imports in GDP evident in the data. In recent years, the greater role of China in the world economy has undoubtedly held down the price of imported manufactured goods, and increased competition may have encouraged domestic firms to be more productive. Such effects, however, would only change the behaviour of marginal costs, and estimates of the new-Keynesian specification, which rely on measures of marginal cost rather than the output gap, should be immune to these issues.[30],[31]
5.4 The Need for a Richer Structural Model
A final possible explanation for apparent flattening in the typical new-Keynesian Phillips curve is that the pricing behaviour of firms has not changed, but that the structural model we have estimated is itself too simple. An example is Ascari (2004), who argues that relaxing the simplifying assumption of no-trend inflation considerably alters the Calvo model. Alternatively, our results suggest that the frequency of price setting may be dependent on the average inflation rate, as price resetting is estimated to have been more frequent in the 1970s than subsequently, an idea also raised by Ball, Mankiw and Romer (1988). This raises a possible indirect way that monetary policy may have influenced the slope of the Phillips curve, namely by achieving lower-trend inflation, it has created an environment in which firms reset their prices less frequently.[32] While we have interpreted the Calvo parameter as a ‘deep’ parameter, really the Calvo framework imposes a constraint on optimal behaviour in order to produce nominal rigidities rather than providing a truly behavioural reason why they occur. Consequently, it is not implausible that the frequency with which prices are reset may be time-varying. To fully investigate this we obviously need a considerably richer structural model. Cogley and Sbordone (2005) estimate a new-Keynesian Phillips curve with trend inflation and allow the parameters to vary over time. They, too, find that the duration of between-price resetting was shortest in the 1970s and longest in the Greenspan era.[33]
Footnotes
Using the labour share for only the non-financial corporate sector (where Corrado and Slifman (1999) argue the data problems are less severe) also suggests that a flattening in the Phillips curve has occurred. [23]
Overhead labour is labour hired independently of the quantity of output produced. [24]
They do, however, note that there appears to have been a sizeable increase in labour's share in the non-financial corporate sector during the late 1960s. [25]
We also assume that the share of firms that use rule-of-thumb pricing, ω, is common across the sectors, which was imposed by Nimark (2007). [26]
This specification ignores imports of intermediate materials. If materials enter the gross output production function ‘isoelastically’, then the materials share is another potential measure of marginal costs (see Rotemberg and Woodford 1999). Batini, Jackson and Nickell (2005) argue that introducing intermediate materials is important for capturing the behaviour of UK inflation. Their model does not use the Calvo framework described above, but is motivated by the quadratic adjustment costs described in Rotemberg (1982). [27]
We use the trimmed-mean CPI adjusted for the introduction of the GST. Nominal unit labour costs are for the non-farm sector. Import prices are measured as the implicit price deflator from the balance of payments, adjusted for changes in average tariff rates, following Beechey et al (2000), using data from Stone, Wheatley and Wilkinson (2005) and Gruen, Robinson and Stone (2005). [28]
This is approximately the share of imports in GDP over the inflation-targeting period. [29]
Sbordone (2007) examines the implications of globalisation in a variant of the new-Keynesian Phillips curve. In particular, she builds on Kimball (1995) to allow the possibility that the increased variety of goods available as a consequence of globalisation alters the market share of each good and hence their price elasticity of demand and the slope of the new-Keynesian Phillips curve. However, Sbordone argues that the observed increase in trade is probably insufficient to have caused a decrease in the slope. [30]
Globalisation may lead to changes in the mark-up, for example, due to sectoral change. This would have a permanent impact on the price level although, as Mishkin (2007a) notes, the effect on inflation should be temporary. [31]
As Sbordone (2007) notes, one could argue that, if globalisation has assisted in creating this low inflation environment through restraining growth in marginal costs, then it has also indirectly contributed to the flattening of the Phillips curve. [32]
Groen and Mumtaz (2008) alternatively argue that the Calvo parameter has not increased. [33]