RDP 2008-02: Combining Multivariate Density Forecasts Using Predictive Criteria 5. Evaluating Density Forecasts
May 2008
Accuracy is obviously a desirable feature of forecasts. For point forecasts, accuracy is usually interpreted to mean that the forecast errors are unbiased and small according to RMSEs. For density forecasts, accuracy can be interpreted in a statistical sense by comparing the distribution of observed data with the forecast distribution. Given a large enough sample of data, if a density forecast is providing an accurate characterisation of the true degree of uncertainty, that is, it provides an accurate description of reality, then we would expect observations to fall uniformly across all regions of the distribution that are forecast to contain the same probability density. As an example, if a density forecast suggests there is a 10 per cent chance of GDP growth falling between 3.5 and 3.7 per cent at a given forecast horizon, then, if economic conditions at the time of forecasting could be replicated 100 times, we would expect 10 actual observations to fall between 3.5 and 3.7 per cent. Diebold et al (1998) employ this result to formally evaluate density forecasts; an approach that avoids both the need to specify the unknown true density and the need to specify a loss function for the user of the forecasts.
Diebold et al's (1998) approach to evaluating univariate density
forecasts is based on the probability integral transform (pit) of a sequence
of n univariate observations 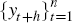 , with respect to the
h-step-ahead density forecasts
, with respect to the
h-step-ahead density forecasts 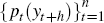 . Each of the transformed
observations or pits
. Each of the transformed
observations or pits 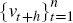 reflects the probability (according to the
density forecast) that an out-turn yt+h will be less than
or equal to what was actually observed. That is,
reflects the probability (according to the
density forecast) that an out-turn yt+h will be less than
or equal to what was actually observed. That is,
Equation (12) links where an actual observation falls relative to the percentiles
of the forecasted distribution. For example, an actual observation that falls
at the median of the density forecast would receive a pit value of 0.5. For
an observation that falls in the upper tail, say at the 90th percentile, the pit value would be 0.9. If a sequence of density
forecasts coincides with the true data-generating process, then the sequence
of pits 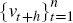 will be uniform U(0,1) and in the case where h = 1,
will be uniform U(0,1) and in the case where h = 1, 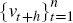 are both U(0,1)
and independently and identically distributed (iid). In other words, if the
density forecasts are not misspecified, over a large enough sample, realisations
should fall over the entire range of the forecasted density and with a probability
equal to the probability specified in the density forecast.
are both U(0,1)
and independently and identically distributed (iid). In other words, if the
density forecasts are not misspecified, over a large enough sample, realisations
should fall over the entire range of the forecasted density and with a probability
equal to the probability specified in the density forecast.
Diebold et al (1999) show that the probability integral transform approach to evaluating density forecasts can be extended to the multivariate case.[7] Let pt(zt+h) again denote a joint density forecast of the 3 × 1 vector of interest zt+h = (z1,t+h z2,t+h z3,t+h)′ made at time t and suppose we have n such forecasts and n corresponding multivariate realisations. After factoring the joint density into the product of conditional densities,
the probability integral transform for each variable in the multivariate realisations can be taken with respect to the corresponding conditional distribution. This creates a set of three pit sequences, each of length n. If the joint density forecasts correspond to the true conditional multivariate density, then these three transformed sequences will each be U(0,1), as will the 3n × 1 vector formed by stacking the individual sequences. As before, in the one-step-ahead case they will also be iid. Since the joint density in Equation (13) can be factored in six ways, there are, in fact, six equivalent pit sequences that can be used to evaluate the multivariate density forecasts.[8]
So evaluating density forecasts can effectively be reduced to testing whether an observed series is U(0,1), and in the case of the one-step-ahead forecasts, whether it is also iid. Before presenting the results, it must be highlighted that in the current context there are reasons why tests of uniformity and independence may be unreliable and it would be unwise to over-emphasise the results from these tests. Given the small sample of data on which we can evaluate the forecasts, it will always be difficult to distinguish between forecasting ability and luck. Also, as Hall and Mitchell (2007), among others, have noted, the way in which dependence in the forecasts affects tests for uniformity is unknown (as is the impact of non-uniformity for tests of independence). And given that serially dependent forecasts are entirely consistent with correctly-specified density forecasts at a forecast horizon greater than one-step-ahead (see Elder et al 2005 for a good discussion of this point), results must be treated with some caution. In addition, formal testing of the densities presented in this paper is further complicated by the fact that we allow for parameter uncertainty when constructing the forecasts.
We present a visual assessment of the hypothesis that the pit-values corresponding to the one-quarter-ahead density forecasts are uniformly distributed in Figure 4. The results for the two- and four-quarter-ahead forecasts are provided in Appendix B (a visual assessment at longer forecast horizons is difficult due to the small number of observations available to evaluate the forecasts). This method is widely used in the literature and may also prove revealing as to how the density forecasts are misspecified. We conduct both a univariate and multivariate evaluation of the BVAR2, FAVAR12 and DSGE models, as well as the two combined density forecasts based on the predictive-likelihood and equal-weighting schemes.
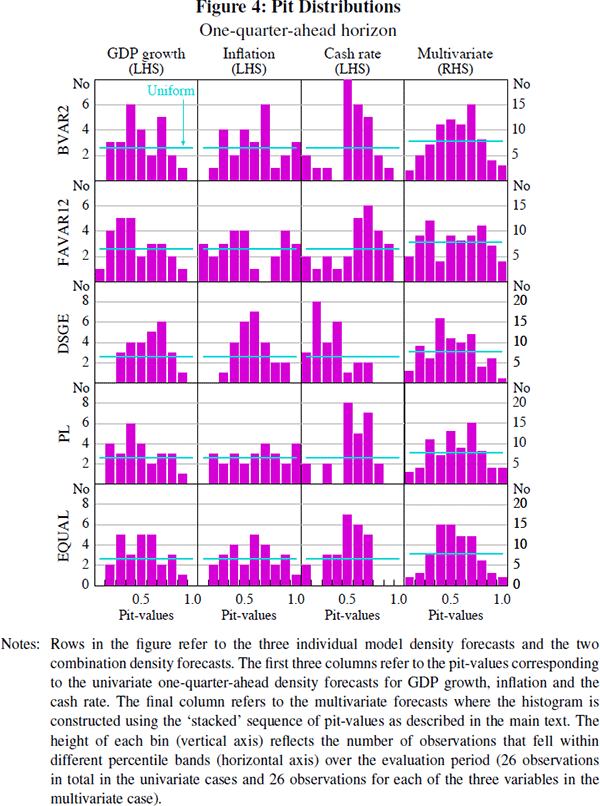
Since a number of observations are ‘used up’ when calculating the predictive-weighting criteria, the effective sample on which we can evaluate the combined densities is reduced. To evaluate the combined one-quarter-ahead density forecasts, 26 observations were available, while only 12 observations could be compared to the combined eight-quarter-ahead density forecasts.[9] To allow for a fair comparison with the predictive-likelihood weighting scheme, this reduced evaluation sample was also used to evaluate the equal-weighting scheme as well as the models individually.
In Figures 4, B1 and B2, the horizontal line represents the theoretical distribution that pit-values would follow in the case of correctly-specified density forecasts.
The ‘closer’ the sample histogram is to this U(0,1) distribution, the ‘better’ the density forecast. A ‘hump’-shaped histogram would be suggestive of density forecasts that are over-estimating the true degree of uncertainty, with too many pit-values close to 0.5 (a result of too many actual observations falling around the centre of the density forecasts over time). A histogram with peaks near 0 and 1, on the other hand, would suggest too small a probability is being assigned to outcomes in the tails of the forecasted distribution.
Some broad conclusions can be taken from the figures. It seems clear that the distributions of pit-values corresponding to the DSGE model's forecasts (the third row in each of the figures) violate the uniformity hypothesis. For both the univariate and multivariate cases, over the evaluation period, the DSGE model's density forecasts were too wide when compared to the actual distribution of observations. The ‘hump’-shaped distribution of pit-values is particularly evident at the two- and four-quarter-ahead forecast horizons (Figures B1 and B2).
Looking at the univariate cases (the first three columns in each figure) it appears that, across the different models and weighting schemes, the density forecasts for inflation perform the best. Apart from the DSGE model, the distribution of pit-values for the inflation forecasts show a reasonable coverage in the tails of the distribution, with the overall distribution typically close to the U(0,1) line. The distribution of the cash rate variable seems to be the most poorly forecast across the various methods. Turning to the multivariate cases, it seems that the FAVAR12 model provides the best description of the joint distribution of GDP growth, inflation and interest rates over the evaluation period. This seems to be true at each forecast horizon. The combination density forecasts constructed using the predictive-likelihood weights also perform well, although it is not clear that the combination density performs that much better than the individual FAVAR12 model's forecasts. There is perhaps some evidence that the optimally combined density forecasts outperform those based on an equal-weighting scheme, although this is most likely due to the poor performance of the DSGE model's density forecasts, which receive one-third weight in the equal-weighting scheme.
Formal statistical tests of the uniformity hypothesis have also been suggested.[10] For example, Berkowitz (2001) suggests taking a further transformation using the standard normal inverse cumulative density function to convert the test for uniformity into a more powerful test for normality. In Appendix B we present a variation of the Berkowitz-type test for normality which aims to allow for serial correlation in the forecasts (see Elder et al 2005). While the test delivers broadly the same conclusion as the visual assessment, given the difficulties faced when assessing the uniformity (or normality) hypothesis discussed earlier, the results should still be treated with some caution.
To test the hypothesis that the pit-values corresponding to the one-quarter-ahead density forecasts are iid, Ljung-Box (LB) tests for up to fourth-order serial correlation are shown in Table 2. LB tests on the first three moments were considered to allow for the possibility of higher-order dependence. Except for the univariate density forecasts for inflation, the tests do show evidence of serial correlation. This suggests that the GDP growth, cash rate and multivariate one-quarter-ahead density forecasts are misspecified to some extent. Taking the multivariate evaluation as an example, the LB tests show dependence in the stacked sequence of pit-values in all of the first three moments when forecasting with the FAVAR12 model. The BVAR2 model seems to fare better, although there is evidence of serial correlation in the second moment. Similarly, pit-values corresponding to the predictive-likelihood and equal-weighting scheme combination density forecasts show evidence of serial correlation in the second moment, which is inconsistent with the hypothesis of correctly-specified density forecasts at the one-step-ahead forecast horizon.
| GDP growth | Inflation | Cash rate | Multivariate | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Moment | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |||
| BVAR2 | 0.07 | 0.36 | 0.04 | 0.78 | 0.70 | 0.95 | 0.66 | 0.04 | 0.08 | 0.90 | 0.00 | 0.66 | |||
| FAVAR12 | 0.19 | 0.62 | 0.39 | 0.20 | 0.56 | 0.20 | 0.01 | 0.21 | 0.03 | 0.00 | 0.06 | 0.01 | |||
| DSGE | 0.77 | 0.79 | 0.55 | 0.85 | 0.99 | 0.96 | 0.14 | 0.99 | 0.25 | 0.00 | 0.27 | 0.07 | |||
| PL | 0.09 | 0.08 | 0.10 | 0.94 | 0.76 | 0.95 | 0.94 | 0.03 | 0.39 | 0.91 | 0.00 | 0.87 | |||
| EQUAL | 0.21 | 0.41 | 0.21 | 0.94 | 0.84 | 0.95 | 0.75 | 0.11 | 0.34 | 0.58 | 0.00 | 0.56 | |||
| Notes: Numbers in the table are p-values corresponding to Ljung-Box tests of up to fourth-order serial correlation in the pit-values. Numbers in bold represent that the null hypothesis is rejected at the 10 per cent significance level. | |||||||||||||||
Overall, based on these results, it is hard to draw strong conclusions about the accuracy of the combined density forecasts. But one result that does seem clear is that the density forecasts constructed using the DSGE model were inconsistent with the data; the density forecasts were too wide when compared with the actual distribution of observations. One possible reason for the large forecast uncertainty implied by the DSGE model could be the many restrictions imposed on the dynamics of the model. If the data ‘disagree’ with these restrictions, larger shocks will be needed to explain the patterns seen in the data and, as a consequence, greater shock uncertainty will be introduced into the forecasts. So while DSGE models have been shown to produce relatively accurate point forecasts (see, for example, Adolfson, Andersson et al 2005), our results suggest they may be less successful at characterising the uncertainty surrounding point forecasts. However, this does not mean that density forecasts from DSGE models are not useful for policy analysis. As structural models with economically interpretable state variables, DSGE models still have the advantage of lending themselves to scenario analysis and ‘story telling’; something that purely statistical models cannot do. This is equally true for density forecasts as it is for point forecasts.
Footnotes
See also Clements and Smith (2000) for an application of the multivariate pit approach. [7]
In the results that follow, the multivariate evaluation was based on factoring the
joint density of zt as follows: 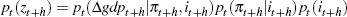 .
[8]
.
[8]
To see this, consider the sequence of eight-quarter-ahead combined density forecasts. The first such forecast can only be made once the first set of eight-quarter-ahead weights are constructed (which is in 2002:Q4). And being an eight-quarter-ahead forecast, it is evaluated against the 2004:Q4 observation. A second eight-quarter-ahead forecast can be made in 2003:Q1 (using an updated set of eight-quarter-ahead weights) and evaluated in 2005:Q1. This pattern continues until the sample is exhausted, which occurs after 12 eight-quarter-ahead forecasts are made. [9]
Corradi and Swanson (2006) provide a detailed summary. See also Hall and Mitchell (2004) for an application of the various testing procedures to density forecasts of UK inflation. [10]