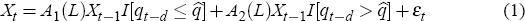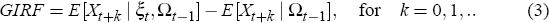RDP 2007-07: More Potent Monetary Policy? Insights from a Threshold Model 2. Methodology

The starting point is to estimate a model to capture relationships between key macroeconomic variables in which nonlinearities can arise by conditioning on the credit regime. In particular, I consider the following two-regime model:

where: X is a vector of endogenous variables; q_t−d is the threshold variable determining the prevailing regime of the system; and ε_t is the vector of disturbances. The indicator function I[·] identifies two separate regimes on the basis of the value of the threshold variable. The delay lag d and critical threshold value 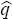are unknown parameters, which have to be estimated along with the parameters A₁ and A₂. The nonlinearity is introduced by allowing the linear structure – given by A₁ and A₂ – to vary across regimes.

I use a set of macro variables, X, that provides a minimal statistical summary of the evolution of the economy:

where: Δγ is real GDP growth; π is CPI inflation; i is the nominal cash rate; and Δcredit is real credit growth. Further details regarding the data and sources are provided in Appendix A.^[5],[6]

The threshold variable (q)is specified as a moving average of quarterly credit growth. The smoothing is applied to avoid an implausible frequency of regime-switching. The order of the moving average is allowed to vary across different specifications from two to four quarters.^[7] Because the threshold variable is constructed as a function of one of the variables in X, it means that shocks to any variable in X can (through an impact on the variable underlying q) induce a shift to a different regime.

The key test of the threshold model given in Equation (1) is whether A₁ ≠ A₂. One complication is that the threshold is not identified under the null of a linear model, but must be estimated under the alternative. In order to test for threshold behaviour, the model is estimated (by ordinary least squares) for values of q over a wide range (with the restriction that at least 10 per cent of the observations fall in each regime, allowing for a reliable test of whether A₁ = A₂). For each possible value of q, a test statistic of no difference between regimes (A₁ = A₂) is calculated (as suggested by Hansen 1996, 1997). Because the distributions of the test statistic are non-standard, the p-values are calculated by bootstrap simulations. If formal tests reject the linear model, the estimated threshold value 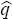is the one that minimises the log-determinant of the variance-covariance matrix of residuals.

It is generally difficult to easily interpret nonlinear time-series models by considering only the estimated parameter values of the model (van Dijk, Franses and Boswijk 2007). Perhaps the easiest way to do this is to analyse the effects of different shocks using nonlinear impulse response functions. These should not be confused with the ‘traditional’ (linear) impulse response function. Gallant, Rossi and Tauchen (1993) and Koop, Pesaran and Potter (1996) point out that in nonlinear models: (i) the effects of a shock depend on the entire history of the system up to the point when the shock occurs; and (ii) the effect of the shock does not need to be proportional to its size. This contrasts with the traditional linear impulse response function, which is conveniently: (i) symmetric (a negative shock of a given magnitude has exactly the opposite effect as a positive shock of the same magnitude); (ii) linear in the sense that the response of the system is proportional to the size of the shock; and (iii) independent of history. The features of nonlinear impulse responses allow the model to change regimes during the simulation period. In order to allow for such switching behaviour, we examine the effects of shocks using the Generalised Impulse Response Function (GIRF).

The GIRF for a specific shock ξ_t (for example, an interest rate shock) and history Ω_t−1 (defined over X's from periods t − 1 and earlier) is

The GIRF is the difference between two conditional expectations of X (which are themselves random variables). For the first term the expectation is conditioned on the particular history and the shock, while for the second term it is conditioned just on the history. The difference between the two yields the dynamic response of the variables in the system at a given horizon, k. The details of the computation of GIRFs are provided in Appendix B.

Footnotes

This specification ignores open-economy considerations for the benefit of parsimony. In a nonlinear model such as used here, each additional variable implies (at least) two extra parameters, adversely affecting the size and power of the linearity tests. I nevertheless checked the robustness of the results to alternative model specifications with open-economy variables. For instance, including US GDP growth to represent world economic activity (as in Dungey and Pagan 2000) did not change the results qualitatively. [5]

Dickey-Fuller tests indicated that inflation and the interest rate series are integrated series. Therefore I also considered a model with these two variables in first differences. The general qualitative features of impulse responses were retained. The impulse response functions, however, tend to revert to zero slightly more rapidly when the analysis is conducted in the first differences. Lanne and Saikkonen (2002) point out that the existence of a unit root may indicate factors not accounted for by linear testing procedures. [6]

The credit variable itself, however, enters the system of equations (X) directly in its original (non-moving-average) form. [7]