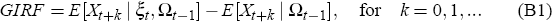RDP 2007-07: More Potent Monetary Policy? Insights from a Threshold Model Appendix B: Computation of the Generalised Impulse Response Function

Appendix B: Computation of the Generalised Impulse Response Function

The method for computing generalised impulse response function follows Koop et al (1996). The GIRF is defined as follows:

The two components of the RHS are conditional expectations of X. The first term is conditional on the shock to the i^th variable and the initial values (the history) of the variables in the model. The second term is conditional only on the history. The GIRF is calculated as follows:

1. Pick a history 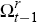, where r = 1,2,3. . .R. The history is the actual value of the lagged endogenous variables at a particular date r (there are as many histories as there are observations in the regime for which the impulse response is computed).
2. Generate residuals (u) by taking bootstrap samples from the estimated residuals (ε) of the model.
3. Using u, 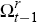and the estimated model parameters A₁ and A₂, simulate the evolution of the threshold model X over k periods. This yields X_t+k(u_t,Ω_t−1).
4. To obtain the first term in the RHS, the previous step has to be modified by adding a shock (ξ) to the i^th variable of the residual of the system. Again, simulate the evolution of the threshold model X over k periods. This gives X_t+k(ξ_t,u_t,Ω_t−1).
5. Repeat steps 2 to 4 B (= 1000) times to get B estimates of X_t+k(u,Ω_t−1) and X_t+k(ξ,u,Ω_t−1). The average over the difference of these estimates gives an estimate of the expectation X for a given history .
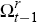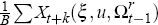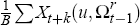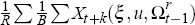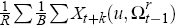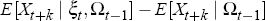6. Repeat steps 1 to 5 R times, that is, repeat the steps for all possible histories the impulse response has to be conditioned on (all the observations in each regime). For R histories this yields R estimates of and . Averaging these over all the histories, that is, and provides estimates of , that is, the generalised impulse response function for a given regime.