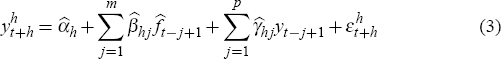RDP 2007-03: Forecasting with Factors: The Accuracy of Timeliness 4. Forecast Accuracy
April 2007
- Download the Paper 296KB
We produce out-of-sample forecasts to assess the accuracy of factor forecasts for our eight macroeconomic series. The factors and forecasting equations are estimated over an in-sample period (initially 1960:Q3–1970:Q1). The estimated factors and forecasting equations are then used to produce forecasts for horizons of two, four and eight quarters from the end date of this in-sample period. The in-sample period is then lengthened by one quarter at a time with forecasts for the three horizons produced at each step. The last forecast is for 2005:Q4, giving a sequence of almost 140 forecasts for each horizon.
Rewriting Equation (2) shows the most general specification of the forecasting equation estimated in this paper:
where  is the vector of q estimated factors at time t, and yt
is the forecast series, which is in log-difference form for all forecast series
except the unemployment rate which is in level form.
is the vector of q estimated factors at time t, and yt
is the forecast series, which is in log-difference form for all forecast series
except the unemployment rate which is in level form.
Because there are numerous ways for determining the number of factors (q) and the number of lags of the factors (m) and the forecast variable (p) included in Equation (3), there are many possible variants of the forecasting equation. Existing studies, such as Stock and Watson (2002a) and Gavin and Kliesen (2006), estimate and present many versions of the forecasting equation. While we also examined the forecasting performance of numerous versions of Equation (3), so as not to overwhelm the reader we present results for just three variants (although those are representative of the broader results). We present the same specifications for all forecast variables to limit any sense of ‘mining’ the numerous models to present more favourable results for each series. The full set of results are available from the authors on request.
The first two specifications are simple, containing a fixed number of factors at each forecast iteration. The model denoted F2 includes just two factors, with no lags of the factors or the forecast variable. The model denoted FAR2 includes two factors (but with no lagged factors) and also allows for the inclusion of up to three lags of the forecast variable (0 ≤ p ≤ 3), with the number of lags selected at each iteration using the Bayesian Information Criterion (BIC). We include two factors as they account for about one-quarter of the total variation in the full data panel. The third specification, denoted FAR-BIC, allows the BIC to select both the number of factors (up to six, 1 ≤ k ≤ 6) and the number of lags of the forecast variable (up to three, 0 ≤ p ≤ 3) at each iteration (again, no lags of the factors are included). This model imposes little structure on the forecasting equation, and so is illustrative of the accuracy of out-of-sample forecasts when there is uncertainty about the appropriate model specification.
We evaluate the accuracy of each forecast model by calculating the mean-squared errors (MSE) of the forecasts for each horizon. We also calculate the MSE of forecasts generated by a simple autoregressive model. This is a commonly used benchmark in out-of-sample forecasting exercises, which has been shown to be difficult to beat, nesting both random walk and constant growth forecasts within the specification. We present our forecast accuracy results as the ratio of the MSE from the factor forecasts to the MSE of the autoregressive forecasts. Numbers less than unity indicate that the factor forecast outperforms the benchmark autoregressive forecast.
4.1 Forecast Accuracy for the Full Panel
Before addressing the issue of timeliness, we demonstrate the performance of factor forecasts using the full data panel. Because all series are included, we do not stack the panel with lags of the series and so the panel used to estimate the factors contains 53 series. Table 2 reports the MSE ratios for the three forecasting equation specifications, at forecast horizons of two, four and eight quarters. Robust standard errors, which account for heteroskedasticity and serial correlation of the forecast errors, are reported in parentheses for each MSE ratio.
| Model | Horizon | |||||
|---|---|---|---|---|---|---|
| Two quarters | Four quarters | Eight quarters | ||||
| GDP growth | ||||||
| F2 | 0.92 | (0.12) | 0.85 | (0.14) | 0.83* | (0.13) |
| FAR2 | 0.96 | (0.17) | 0.89 | (0.17) | 0.84 | (0.14) |
| FAR-BIC | 1.10 | (0.14) | 1.02 | (0.16) | 0.78* | (0.14) |
| Non-farm GDP growth | ||||||
| F2 | 0.78** | (0.12) | 0.76* | (0.15) | 0.73* | (0.17) |
| FAR2 | 0.86 | (0.15) | 0.87 | (0.14) | 0.74* | (0.17) |
| FAR-BIC | 0.95 | (0.14) | 0.93 | (0.14) | 0.78* | (0.15) |
| Private final demand growth | ||||||
| F2 | 0.82* | (0.12) | 0.71** | (0.15) | 0.77* | (0.15) |
| FAR2 | 0.78** | (0.13) | 0.67** | (0.17) | 0.73* | (0.17) |
| FAR-BIC | 0.81* | (0.13) | 0.74* | (0.18) | 0.80 | (0.16) |
| Household final consumption expenditure growth | ||||||
| F2 | 0.90* | (0.07) | 0.69*** | * (0.11) | 0.64** | (0.16) |
| FAR2 | 0.97 | (0.08) | 0.69*** | (0.11) | 0.65** | (0.16) |
| FAR-BIC | 1.20 | (0.26) | 0.97 | (0.21) | 1.00 | (0.26) |
| Employment growth | ||||||
| F2 | 0.76** | (0.14) | 0.71** | (0.16) | 0.77* | (0.17) |
| FAR2 | 0.78** | (0.13) | 0.76* | (0.17) | 0.80 | (0.18) |
| FAR-BIC | 0.82* | (0.12) | 0.84 | (0.14) | 0.81 | (0.17) |
| Unemployment rate | ||||||
| F2 | 16.02 | (4.06) | 4.08 | (2.65) | 1.80 | (0.61) |
| FAR2 | 0.67** | (0.16) | 0.71** | (0.16) | 0.76** | (0.13) |
| FAR-BIC | 0.58** | (0.19) | 0.70** | (0.17) | 0.71** | (0.15) |
| CPI inflation | ||||||
| F2 | 1.78 | (0.56) | 1.63 | (0.40) | 1.14 | (0.22) |
| FAR2 | 0.89 | (0.12) | 0.84 | (0.16) | 0.71* | (0.20) |
| FAR-BIC | 1.01 | (0.20) | 0.78 | (0.21) | 0.63* | (0.28) |
| Building approvals growth | ||||||
| F2 | 1.09 | (0.10) | 1.04 | (0.09) | 0.94 | (0.11) |
| FAR2 | 1.01 | (0.08) | 1.04 | (0.09) | 0.98 | (0.12) |
| FAR-BIC | 0.98 | (0.09) | 0.98 | (0.09) | 1.01 | (0.11) |
| Notes: Model F2 includes two factors and no lags of the forecast variable. Model FAR2 includes two factors and up to three lags of the forecast variable, selected at each iteration using the BIC (0 ≤ p ≤ 3). Model FAR-BIC uses the BIC to select both the number of factors (up to six, 1 ≤ k ≤ 6) and the number of lags of the forecast variable (up to three, 0 ≤ p ≤ 3) at each iteration. Numbers in parentheses are robust standard errors calculated using the delta method. Ratios significantly less than 1 at the 1, 5 and 10 per cent confidence levels are indicated by ***, ** and *. | ||||||
For the majority of series and forecast horizons, the MSE ratio is less than unity, indicating that the factor-based forecasts outperform benchmark autoregressive forecasts. For example, the MSE ratio of 0.85 for the F2 model of GDP growth at a four-quarter horizon indicates that the factor forecast has a 15 per cent lower MSE than the autoregressive forecast. Although most MSE ratios are not significantly less than unity at the 5 per cent level of significance, just under half are at the 10 per cent level of significance.
The results in Table 2 show that the MSE ratio is generally lowest for horizons of four and eight quarters (with the unemployment rate a notable exception). This finding that the gains in forecast accuracy are greatest at these longer horizons is consistent with the literature. Note that this does not mean that the factor forecasts are more accurate at longer horizons than at shorter horizons; the absolute MSE of factor forecasts does increase with the horizon of the forecast (not shown). Rather, this result highlights the tendency for factor forecasts to be more accurate relative to the autoregressive forecasts at longer horizons. The improvement in forecasting performance over the autoregressive benchmark is most important from a policy perspective at longer horizons, in part because alternatives – including the use of partial indicators and the importance of recent shocks – are often available for making reasonable short-horizon forecasts.
For the four national accounts series (the first four series in Table 2) and employment, the simple models (F2 and FAR2) which keep the number of factors fixed produce more accurate forecasts than the more complex model which selects the number of factors at each forecast iteration. In general, the simplest model (F2), which maintains the same forecasting equation specification at each iteration, is slightly more accurate. This result contrasts with the poor forecasting performance of the F2 model for consumer prices and the unemployment rate; at all horizons it is less accurate than the benchmark autoregressive forecast. For these two series the inclusion of lags of the forecast variable in the forecasting equation is important for forecast performance as demonstrated by the lower MSE ratios of the FAR2 and FAR-BIC models. The unemployment rate and inflation have both had long cycles and have likely experienced substantial structural change over the 45-year sample. The factors capture the general state of the economy rather than structural change, and so it is necessary to include lags of the forecast variable to account for any structural change.[4] For the building approvals series, all three models produce forecasts that are no better or worse than the benchmark autoregressive forecast. Surprisingly, the current state of the overall economy (as indicated by the factors) seems to have little information for forecasting building approvals.[5]
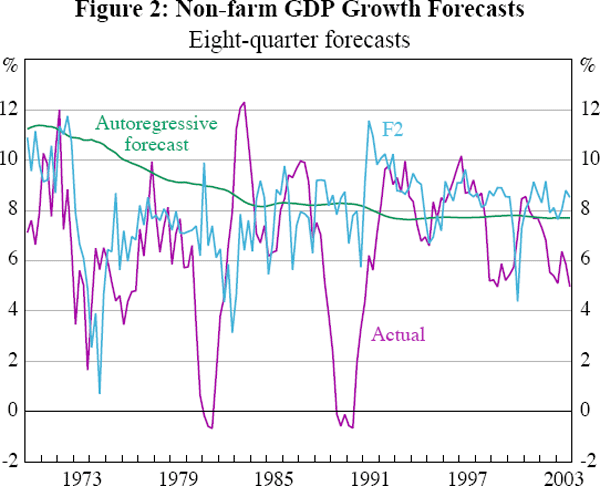
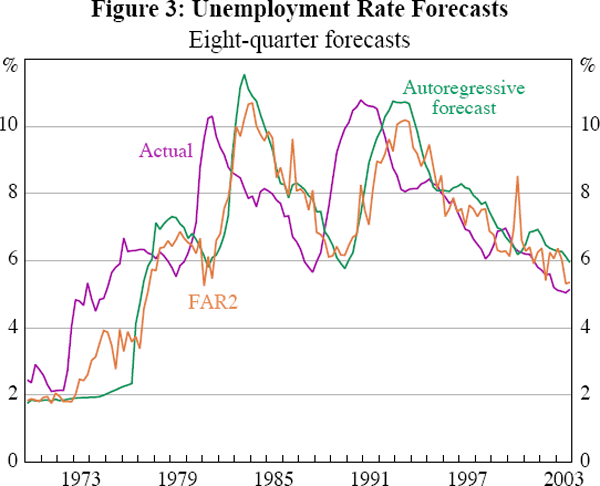
To give an indication of the out-of-sample forecasting performance of the factor-based models, Figures 2 and 3 illustrate respectively the forecasts for eight-quarter growth in non-farm GDP (using the F2 forecast equation specification) and the level of the unemployment rate eight quarters ahead (using the FAR2 specification). The autoregressive forecasts for each series are also shown. For non-farm GDP, the autoregressive forecast chosen by the BIC is a simple average of growth of non-farm GDP in the in-sample period. Clearly, the factor-based forecasts are able to capture a substantial amount of variation in the forecast series over and above the autoregressive forecasts. In contrast, for the unemployment rate the factor forecast is very similar to the autoregressive forecast, demonstrating the importance of lags of the forecast variable in forecasting this series.
4.2 Panel Timeliness and Forecast Accuracy
The results in Table 2 demonstrate that factor forecasts can outperform benchmark autoregressive forecasts for many key macroeconomic series. But the breadth of the panel used to generate these factors comes at the expense of including less timely series. As Figure 1 shows, many series have a publication lag of two months or more. In this section we examine how forecast accuracy changes if more timely data are used to generate the factors. To do this, we reproduce the forecasting exercise in Section 4.1 using progressively broader, but less timely, data panels. As outlined in Section 2.3, we include one lag of every series, along with the series that are available at each publication date. This method incorporates the broadest range of up-to-date data. We start with out-of-sample forecasts based on data available 24 days before the end of each quarter. Hence, the panel consists of 57 series: the one-period lag of all 53 series and up-to-date values for the four survey series. We repeat the exercise based on data available at the end of the quarter, allowing us to incorporate an extra three financial market series. We continue this process by moving along the timeline of release dates shown in Figure 1, progressively expanding the number of series included in the panel until it contains 106 series: the one-period lag and up-to-date values for each of the 53 series. With this sequence of out-of-sample forecasts we can then examine how the MSE ratio changes as the forecasts become less timely but the panel uses a more comprehensive set of information.
One important consideration in this exercise is when the base quarter data for the series being forecast become available. For example, the information set used to forecast CPI inflation 20 days after the end of the base quarter will not contain the CPI release for the base quarter, while that used 30 days after the end of the base quarter will. Clearly this adds to the breadth of the panel used to estimate the factors, but it also enables a more up-to-date lag to be included in the autoregressive terms. Our factor forecasts account for this, so that the FAR2 model only contains autoregressive lags 1–2 before the release date of the series being forecast, but contains lags 0–2 after the release date. However, to simplify the interpretation of the change in forecast accuracy as the breadth of the panel changes, we allow the benchmark autoregressive forecast to always use the base quarter release of the series. This means that the denominator of the MSE ratio does not change along with the timeliness of the forecast. Because of this, the MSE ratio before the release of the forecast series does not represent a fair test of forecast accuracy as the factor forecast does not use the base quarter's value of the forecast series while the benchmark autoregressive forecast does.
The MSE ratios for four- and eight-quarter-ahead forecasts are plotted against forecast timeliness – the number of days from the end of the base quarter that the forecast is made – in Figures 4–11. For each figure, moving from left to right presents the MSE ratio when forecasts become less timely, but consequently use more series to estimate the factors.[6] Beyond the release date of the series being forecast (shown as a vertical dashed line), the forecasts also use one extra autoregressive lag as required. For clarity, the FAR2 specification results are not shown in Figures 4–9 since they are very similar to the F2 results. For the unemployment rate and CPI forecasts, the FAR2 specification substantially outperforms the F2 specification (as discussed below and in Section 4). So for these two series, the FAR2 results are shown in place of the F2 results (Figures 10–11).
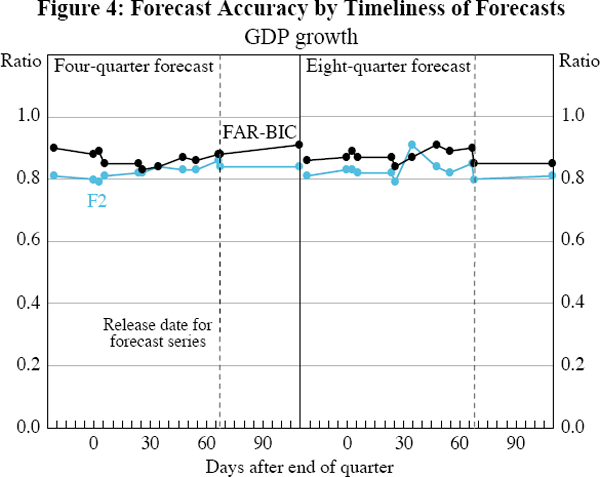
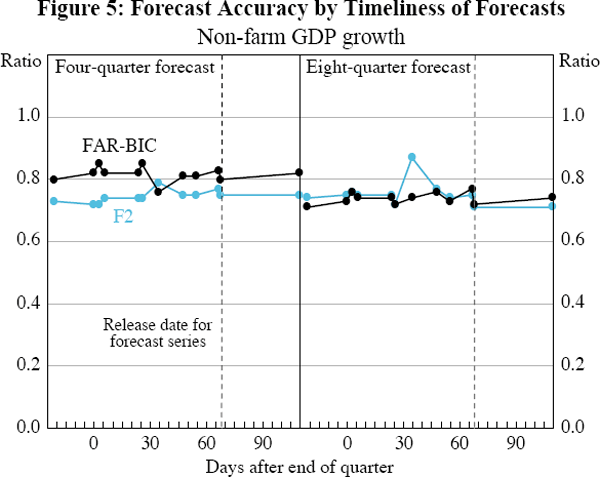
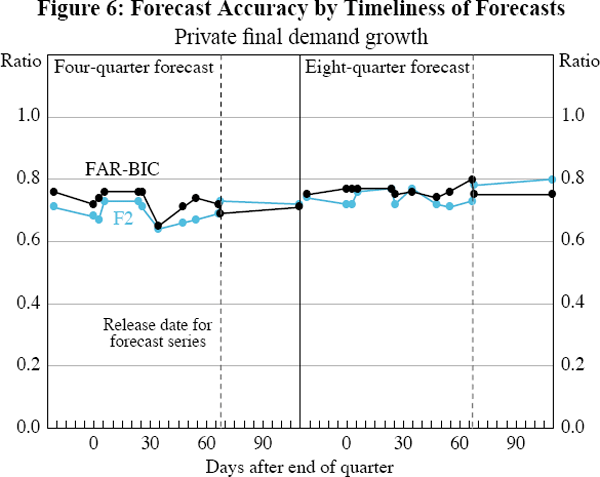
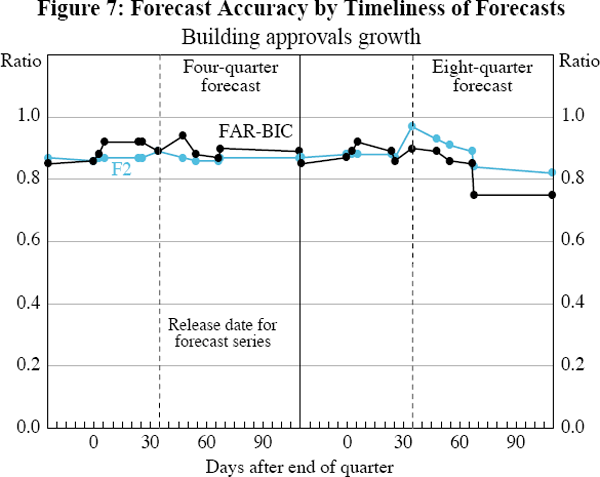
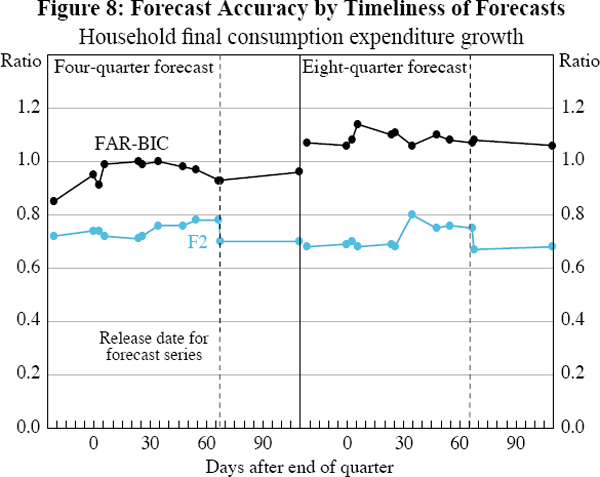
The forecasting performance of the factor models is similar for three of the national accounts series – GDP, non-farm GDP and private final demand – and building approvals (Figures 4–7). In each case the MSE ratios for both the F2 model and FAR-BIC model are always less than 1, demonstrating that the factor forecast is more accurate than the autoregressive forecast. Note that this is even more impressive in light of the fact that the autoregressive forecast uses the most recent quarter's value for the forecast series prior to its release date, while the factor forecast does not. For these series, the MSE ratio tends to be around 0.8 (though with a range from around 0.65 to 0.85), indicating that the factor forecasts are around 20 per cent more accurate than the autoregressive forecast.
The other striking feature for all four of these series, at both the four- and eight-quarter horizons, is that the MSE ratios do not have a discernable trend. This indicates that the accuracy of the forecasts does not change substantially (for better or worse) as the data panel is expanded to incorporate the additional series that become available. For these series there is no deterioration in forecast accuracy when forecasts become more timely. This is perhaps not surprising as Gillitzer et al (2005) showed that the factors using a similar data panel to that employed here are highly persistent. Since the factors derived from a given quarter's data are very similar to the factors derived from the following quarter, the forecasts based on those factors, and so their errors, are also very similar.
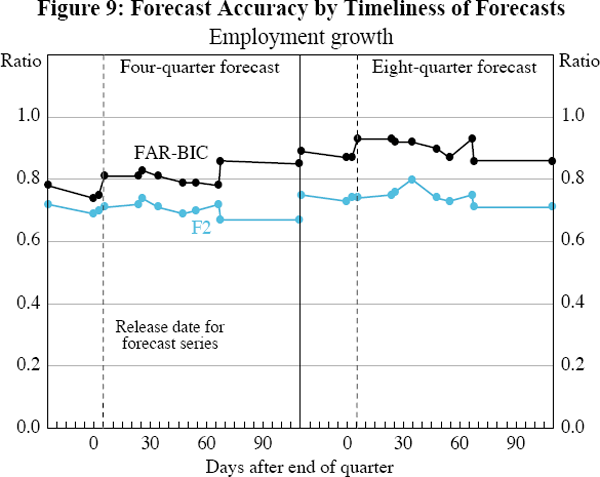
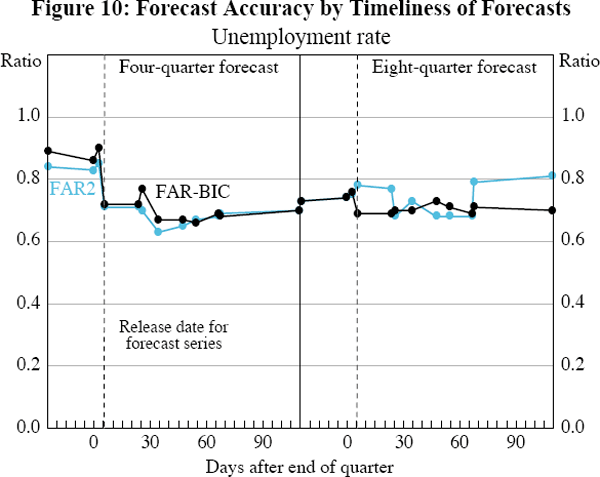
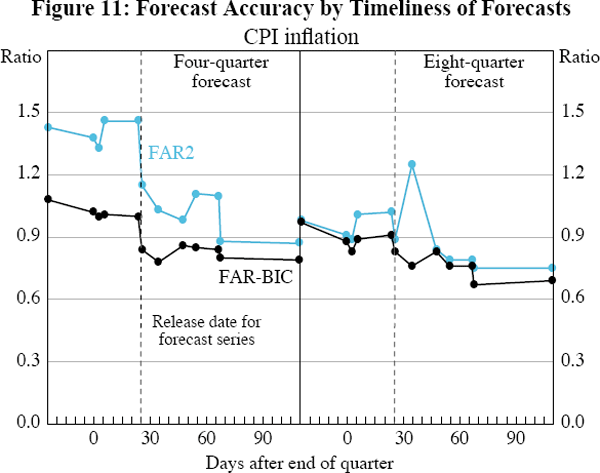
For the other four series – household final consumption expenditure, employment, the unemployment rate and CPI inflation – there are greater differences in the forecast accuracy, across factor models as well as with timeliness (Figures 8 and 11).
For household final consumption expenditure and employment, the simpler two-factor models (F2 and FAR2) are consistently more accurate than the more complex FAR-BIC model. Recall that at each iteration the FAR-BIC model chooses the number of factors and lags of the forecast variable to include in the forecast equation. It is not the inclusion of autoregressive terms that leads to this deterioration in forecast performance; in all three cases the FAR-BIC underperforms relative to the FAR2, which includes autoregressive terms (not shown). Rather, the deterioration in forecast performance is due to the model changing the number of factors at each forecast iteration. The only series for which the FAR-BIC model outperforms the simpler models is CPI inflation. This suggests that for most series, the FAR-BIC model has a tendency to over-fit the data in the period used to estimate the forecasting equations. In contrast, there appear to have been greater structural changes to the inflation process over the long sample, meaning that the changing structure of the FAR-BIC model produces more accurate forecasts. Overall, these results demonstrate that there are benefits to a parsimonious factor model that keeps the number of factors constant.
For both employment growth and the unemployment rate, the MSE ratios for both factor models are always less than one (as they are for GDP, non-farm GDP, private final demand and building approvals), demonstrating that these models produce more accurate forecasts than the autoregressive models. This also applies for most of the forecasts of household final consumption expenditure, with the exception of the FAR-BIC forecasts at an eight-quarter horizon. For CPI inflation at the four-quarter horizon, the MSE ratio for both factor models is initially greater than one, indicating that the factor model forecasts are less accurate than the simple autoregressive model. However, as the forecasts become less timely, and so the data panel used to calculate the forecasts includes more information, the forecast accuracy of the factor models improves and eventually exceeds that of the autoregressive forecasts. The factor model forecasts are generally more accurate relative to the autoregressive forecasts at the eight-quarter horizon than at the four-quarter horizon. These longer horizon forecasts for CPI inflation also tend to become more accurate as the data panel expands.
For two of the series, the unemployment rate and CPI inflation, there is a sharp improvement in the factor forecasts when the base quarter's value of each of these series is included in the information set used for their forecasts; that is, the MSE ratio steps down at the vertical dashed line. As discussed in Section 4, these two series have had long cycles and appear to have experienced considerable structural change. As a result, the FAR2 model, which includes autoregressive lags along with the two factors, substantially outperforms the simpler F2 model that excludes autoregressive lags. The usefulness of autoregressive lags apparently carries through to those lags being more timely, hence the step down in the MSE ratio for both factor models when the base quarter's lag becomes available.
There is one caveat to our observation: that, for most series, forecast accuracy does not improve markedly with broader but less timely panels. For four of the series – household final consumption expenditure, employment, CPI inflation and building approvals – there is some evidence of a small improvement in forecast accuracy of the factor models, as indicated by the step down in the MSE ratio when the national accounts series are included in the panel 68 days after the end of the base quarter.
Footnotes
Because of these long cycles and likely structural change, the sum of the autoregressive coefficients is close to unity. [4]
Interest rates are not included in the data panel as market-determined interest rates are not available for the full sample. Potentially, over a shorter sample, factors from a panel that includes interest rates would be more successful in forecasting building approvals. [5]
The ACCI-Westpac survey data are released before the previous quarter's national accounts. In forecasting the national account variables we include the previous quarter's national accounts data in the information used. In effect this means the first forecast would be made around one week after the ACCI-Westpac data are actually released. Similarly, the building approvals release has a publication lag of around 108 days, meaning that at the end of the base quarter it is not yet available for the previous quarter. Despite this we include it in our panel for completeness. Excluding it does not significantly alter the results. [6]