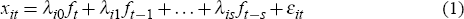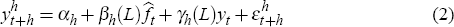RDP 2007-03: Forecasting with Factors: The Accuracy of Timeliness 2. Factor Models and Timely Forecasting

The process of using factors to forecast can be broken down into two steps. First, a panel of data is used to estimate the factors. Second, these factors are used to produce out-of-sample forecasts for the series in question. In this section we explain the estimation of the factors and the forecasting equation, though because these techniques have been discussed elsewhere, for example Boivin and Ng (2005), we only provide a brief exposition.

2.1 Estimating the Factors

The data used to estimate the factors are assumed to have an approximate factor representation, given by Equation (1),

where x_it is the time t observation of series i of the data panel, λ_ij is a vector of series-specific factor loadings for lag j of the factors, f_t is a vector of q factors common across all series and ε_it is a series-specific idiosyncratic error term (which may be weakly correlated across time and series).

To estimate the factors we use the method demonstrated by Stock and Watson (1999; 2002a; 2002b). Given the simple representation presented by Equation (1), the factors and loadings can be estimated by calculating the principal components of the data panel. If Equation (1) includes lags, then the factors are estimated by principal components of a matrix that augments the data panel with lags of the data panel; for example, if the matrix of the x_it is denoted by X and one lag is included, then the principal components are calculated from the matrix that concatenates the matrix of data from time 0 to T − 1 with that from time 1 to T, that is, X_[0,T−1]|X_[1,T].

2.2 Forecasting

The second step involves including the estimated factors in a forecasting regression. Various specifications of the forecasting equation have been used in the literature. We focus on a simple one that can easily be used for our iterative process in which we use panels with varying numbers of series, and has typically been found to produce forecasts that are at least as good as other specifications. The series being forecast, 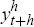, is regressed on current and lagged estimates of the factors, 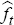, and lags of itself, as in Equation (2).

We use the notation 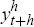to show that the dependent variable is the h-period percentage change of the series being forecast (the one exception is the unemployment rate for which we use the h-period ahead level). The lags on the right-hand side of the equation, γ_h(L)y_t, are one-period percentage changes (or the level for the unemployment rate). All percentage changes are approximated by log differences. As Boivin and Ng (2005) demonstrate, including autoregressive terms (lags of the dependent variable) along with the factors is equivalent to forecasting using the factors and the lagged idiosyncratic terms, ε. After estimating Equation (2), the forecast is then generated using the parameter estimates.

In Appendix B we compare the performance of the forecasts generated using this methodology with forecasts that use the ‘dynamic’ factors estimated by the technique of Forni et al (2005) and a non-parametric technique developed by these authors. The simpler methodology employed here is shown to produce forecasts that are at least as good as those using these more complex procedures. This result is in line with other studies, for example Boivin and Ng (2005).

2.3 Timeliness of the Data Panel

The time it takes for data for a given quarter to be released varies across different macroeconomic series. Consequently, as more time passes since the last quarter of the in-sample period, which is the base quarter from which the forecasts are made, an increasing number of series will have an observation for that quarter. To examine the trade-off between forecast accuracy and timeliness we estimate the factors and forecasts recursively using data panels expanded to include the increasing number of series that become available as the number of days since the end of the base quarter increases. This enables us to examine how forecast accuracy changes as we wait for more series to become available so that a broader panel can be used to estimate the factors.

In order to incorporate the lagged information that is contained in these series for which the base quarter's data are not available, we use a pseudo stacked panel that includes the one-period lag of all series and the contemporaneous values for the series that have been released.^[2] For example, if the panel X contains 50 series, but only 20 of these have been released one month after the end of the base quarter, then the full matrix from which we estimate the factors at this time contains 70 series and is 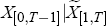, where 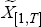is the matrix representing the panel of these 20 available series. 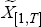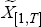The iterative procedure of expanding the panel breadth starts with the release of the first series, when contains just 1 series, and proceeds until all the series have been released and so contains all 50 series, and is the same as X_[1,T].

Footnote

An alternative approach would be to impute the missing observations using the expectations maximisation algorithm described by Stock and Watson (2002b). However, this technique does not tend to produce reliable estimates for missing observations. [2]