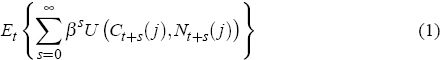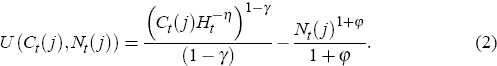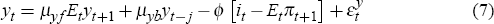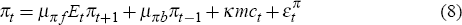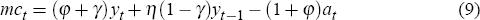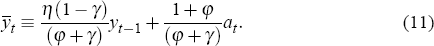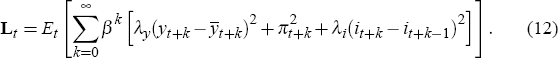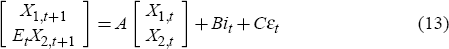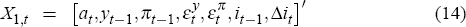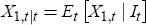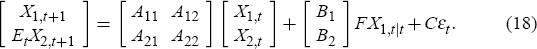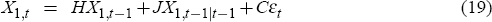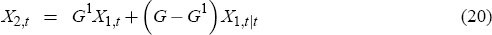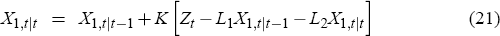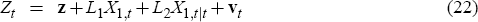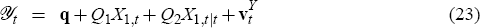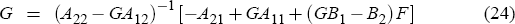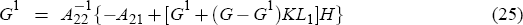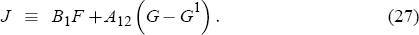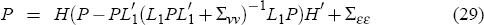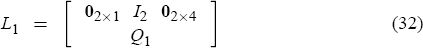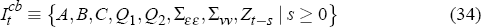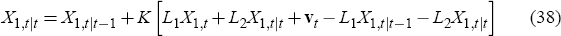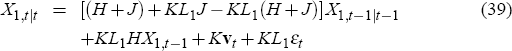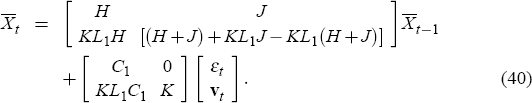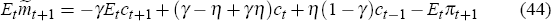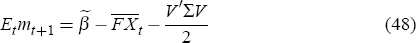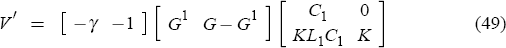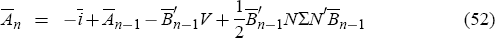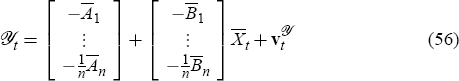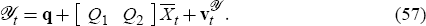RDP 2006-05: Optimal Monetary Policy with Real-time Signal Extraction from the Bond Market 2. The Macroeconomy, the Term Structure and Monetary Policy Under Imperfect Information

This section presents a model where the central bank extracts information about the state of the economy from the term structure of interest rates. Movements in the term structure will then have a direct impact on the macroeconomy through its effect on the central bank's estimate of the state and therefore also on the setting of the policy instrument. This means that the macroeconomy, the term structure model and the filtering problem of the central bank have to be solved simultaneously. This makes the model different from other recent papers, for example Hördahl et al (2006) and Wu (2002), where the macroeconomic model can be solved separately from the term structure. Here, the macroeconomy is described first without specifying an explicit interest rate function, but merely noting that it is set by the central bank to minimise a loss function that in principle could be derived from micro foundations. The filtering problem of the central bank is then solved, taking the term structure model as given. Finally, in the last part the term structure model is derived and it is demonstrated how it influences the dynamics of the macroeconomy through an information channel.

2.1 The Macroeconomy

We use a standard business cycle model of the macroeconomy with monopolistically competitive firms that sell differentiated goods. Prices are set according to the Calvo mechanism, with a fraction of firms using a rule of thumb rather than optimising as in Galí and Gertler (1999). Households supply labour and consume goods. In addition to their own current consumption, they also care about the lagged aggregate consumption level.

2.1.1 Households and firms

Consider a representative household j ∈ (0,1) that wishes to maximise the discounted sum of expected utility

where β ∈ (0,1) is the household's subjective discount factor and the period utility function in consumption C_t and labour N_t is given by

The variable H_t

is a reference level of consumption that we interpret as external habits that makes marginal utility of consumption an increasing function of lagged aggregate consumption. The habit specification helps to explain the inertial movement of aggregate output as well as the procyclicality of asset prices.^[2] Differentiated goods indexed by i ∈ (0,1) are produced with a technology that is linear in labour and subject to a persistent productivity shock A_t

that follow an AR(1) process in logs

Firms set prices according to the Calvo (1983) mechanism where a fraction θ of firms reset their price in a given period. Of the firms resetting their price, a fraction (1–ω) optimise their price decision and take into account that their price may be effective for more than one period while a fraction ω of price-setters use a ‘rule of thumb’ as in Galí and Gertler (1999). The ‘rule of thumb’ price-setters set their price equal to the last period's average reset price plus the lagged inflation rate.

2.1.2 The linearised model

The linearised structural equations are given by Equations (7) and (8)

where {y_t, π_t, i_t} is real output, inflation and the short nominal interest rate in period t. The coefficients {μ_yf, μ_yb, μ_πf, μ_πb, ø, κ } are derived from the utility function (2) and the parameters in the price-setting equation are specified in the Appendix. Marginal cost in period t, mc_t, can be found by equating the marginal utility of consuming the real wage paid for an additional unit of labour with the household's disutility of providing the additional unit of labour. The real marginal cost then equals the market-clearing real wage divided by productivity

where the relationship

was used to substitute out labour supply. Potential output, , defined as the level of output that is compatible with no acceleration in inflation, then is

The short-term interest rate is set by a monetary authority to minimise the expected value of the loss function

The weights λ_y and λ_i can be chosen such that the loss function (12) is a second-order approximation of the utility function of the representative agent.^[3] However, we do not necessarily want to impose this restriction when we estimate the model. Equations (5), (7), (8) and (9) can be written more compactly as

where

2.2 Monetary Policy and Real-time Signal Extraction

Monetary policy operates in an uncertain environment where some state variables are only observed with error and delay, and some variables, like productivity and thus potential output, are not observed at all. Variables that are not observable but relevant for monetary policy have to be inferred from the variables that are observable. In such a setting, Svensson and Woodford (2004) show that a form of certainty equivalence holds. That is, with a quadratic objective function and linear constraints, the optimal interest rate can be expressed as a linear function of the central bank's estimate of the state X_1,t|t

where I_t is the information set of the central bank at time t. The coefficients in the policy function are then the same as they would be if the central bank could observe the pre-determined state perfectly. The coefficient vector F of the optimal interest function

can thus be found by standard full-information methods, for instance by the algorithm in Söderlind (1999). Here we describe how the central bank can apply the Kalman filter to estimate the state X_1,t. The affine function that maps the pre-determined state into bond prices, characterised by the matrices Q₁ and Q₂, is taken as given and deriving the equilibrium dynamics of the model is then a straightforward application of the procedure in Svensson and Woodford (2004).

Partition the coefficient matrices in (13) conformably to the pre-determined and forward-looking variables and substitute in the interest rate function to get

The equilibrium dynamics of the model can then be described by Equations (19)–(23)

where Z_t is the vector of variables that are observable to the central bank and 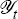is a vector of bond yields of different maturities. The system of Equations (19)–(23) can be written solely as functions of the actual state, the central bank's estimate of the state and the shock vectors ε_t and ν_t. The coefficient matrices G and G¹ are derived in Svensson and Woodford (2004) and satisfy Equations (24) and (25)

where the following definitions were used

The Kalman gain matrix K is given by

where P is the one-period-ahead forecast error, Σ_εε is the covariance matrix of the structural shocks 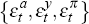and Σ_νν is the covariance matrix of the errors in the measurement Equation (22). The coefficient matrices G, G¹, the Kalman gain K and the one-period forecast error P have to be determined jointly by finding a fixed point of the system described by the Equations (24), (25), (28) and (29). Before we can solve for the equilibrium dynamics we need to specify the selection matrices L₁ and L₂ in the observation Equation (22). We thus have to decide what the central bank can observe.

2.2.1 Variables observable by the central bank

The central bank observes bond yields contemporaneously, while output and inflation are only observable with a one-period lag. This is a compromise that is necessary due to the division of time into discrete periods that do not conform to the exact delays of data releases, though it does capture some essential features of data availability. Data on real GDP are released with a significant delay while bond prices are observed every day that bonds are traded. The compromise is the observation of the price level. CPI data are usually released the month after observation so the one-quarter lag is thus too long for most countries.^[4] We can write the measurement Equation (22) as

and the matrices L₁ and L₂ are then given by

The information set of the central bank is given by

that is, in addition to observing the vector Z_t, the central bank also knows the structure of the economy.

2.3 The Law of Motion for the State of the Economy

In full-information models, the relevant state for the pricing of bonds is simply the same as the state of the economy. In the present model the central bank cannot observe the state of the economy with certainty and uses the Kalman filter to estimate it. The central bank's information set is a subset of the information set of the bond market participants. This assumption allows us to model bond market participants as if they know the central bank's estimate of the state. We define the extended state 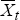as

and we want to find a system of the form

that is, we conjecture that yields are an affine function of the extended state plus a noise term 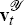. We start by substituting the observation Equation (22) into the central bank's, updating Equation (21) to get

Using Equations (19)–(21), definitions (26) and (27) and rearranging them, we get

The matrices K, L₁ and L₂ depend on the coefficients in the conjectured term structure function (23) and the covariance matrix of measurement errors/non-macro factors 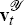denoted by 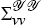. Combining Equations (19) and (39) we get the conjectured form from Equation (36)

2.4 The Term Structure and the State of the Economy

In this section we derive the law of motion for the nominal stochastic discount factor that is used to price the bonds from the utility function of the representative household. However, the framework presented here is general enough to accommodate any affine asset-pricing function and it is thus not necessary to impose that the macro model and the bond pricing function are determined by the same underlying micro foundations. Define the nominal stochastic discount factor M_t+1 as

where U_ct is the marginal utility of consumption in period t. If we assume that the distribution of M_t+1 is log normal, that is, if m_t+1 = logM_t+1 and

then the expected value of m_t+1 is

Plugging in the utility function (2) into (41) and (43) we get

where 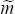denotes the deviation of m from its mean. Using that in equilibrium

must hold and that the interest rate i_t is a function of the state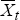

we get the following simple expression for the the expected value of m_t+1

where V′ and Σ in the variance term is given by

The log of the price at time t of a nominal bond paying one dollar in period t + n will then be

where the constant 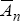and the vector 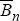are given by the recursive relations

starting from

where 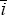is the average short interest rate. To find the vector of yields of selected maturities 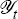, collect the appropriate constants 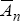and vector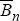s as

where the yield of an n periods to maturity bond is found by dividing the price by n. Partitioning the stacked vectors 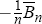appropriately gives the desired form

Equation (57) has a dual interpretation. On one hand it can be used to express bond yields as a function of the state and the vector of shocks to the term structure, 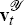, are then residuals, i.e., the component of the yields that cannot be explained by the state. A small variance of 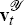should then be interpreted as that the term structure model provides a good fit of the observed yields. Equation (57) can also be viewed as a measure equation of the state. The vector of shocks 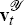are then measurement errors and when the variance of 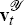is small, the signal-to-noise ratio is high and the term structure is very informative about the state of the economy. In the special case of the rank of Q₁ being equal to the dimension of the state and 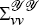= 0, the model replicates the full-information dynamics, since the state can then be backed out perfectly from the term structure. In the opposite case, when the variances of 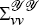are very large, the model will replicate the dynamics when the central bank can only observe imperfect but direct measures of the lagged aggregate variables.

Footnotes

See Campbell and Cochrane (1999) for the implications of habits for asset prices. [2]

See Amato and Laubach (2004). [3]

One exception is Australia, where data on the CPI are collected quarterly. [4]