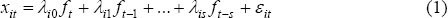RDP 2005-07: The Australian Business Cycle: A Coincident Indicator Approach 3. The SW and FHLR Methodologies
October 2005
- Download the Paper 1.72MB
Both the SW and FHLR methodologies assume that economic time-series data have an approximate factor representation. That is each series, xit, can be represented by Equation (1)
where ft is a vector of the q (unobserved) mutually orthogonal factors at time t, λij is a row vector of factor loadings on the jth lag of the factors and εit is the idiosyncratic residual. All of the series, xi, are expressed in stationary form. For most series, this involves taking the first difference of the log of the monthly or quarterly series. Hence, the factors that emerge from these models can be thought of as monthly or quarterly growth rates. To ensure that the relative volatility of individual series does not affect their importance in estimating the factors, all series are transformed to have zero mean and unitary standard deviation. Equation (1), often referred to as a dynamic factor model, is an approximate factor model in that the residuals, εit, are allowed to be weakly correlated through time and across series. This differs from the older style of exact factor models in which the residuals are uncorrelated in both dimensions. The common component of series i is that part that can be explained by the factors, and so is equal to the difference between the actual value and the idiosyncratic residual, (xit – εit).
Where the SW and FHLR methodologies differ is in how they estimate the factors and factor loadings. SW is estimated in the ‘time domain’, while FHLR is estimated in the ‘frequency domain’. SW estimates the loadings and factors by calculating the principal components of the series. To include lags of the factors, the model is estimated using a ‘stacked panel’, that is, augmenting the data matrix X (the matrix of the xit) with lags of itself. In doing so, SW estimates ft−1 and ft as separate sets of factors, implying that the model has r=q(s+1) separate factors.
While SW uses the eigenvalues and eigenvectors of the covariance matrix of the data (principal components) to calculate the factors and loadings, FHLR obtains the factors and loadings by first calculating the eigenvalues and eigenvectors of the spectral density matrix of the data. By using the spectral density matrix, FHLR explicitly accounts for any leading or lagging relationships among the variables. The FHLR index also removes high-frequency volatility, a step that is possible because FHLR constructs sample estimates of the spectral density matrix of the panel of data.[1] This results in a smoother index.
Because of these differences in the estimation methodologies, SW is often referred to as being a ‘static representation’ of the factor model while FHLR is referred to as being a ‘dynamic representation’. As noted, FHLR explicitly takes into account the possibility of leads and lags in the relationship, while SW treats lagged factors as separate factors. Since FHLR effectively aligns the data to estimate q factors, rather than r factors as in SW, it should be more efficient. This advantage of FHLR comes at the expense of additional complexity in estimation, including the need to decide on values for some estimation parameters (for example, to obtain a sample estimate of the spectral density matrix). SW is typically estimated as a one-sided filter (that is, it uses only lagged data), while FHLR is a two-sided filter, using both leads and lags in its construction. As a result, while SW will truncate the beginning of the sample if lags are included, FHLR will truncate both the beginning and end of the sample. In fact, the FHLR methodology typically uses a longer window to estimate the lagging relationships and so will truncate more of the beginning of the sample. These differences are less of an issue for the historical analysis in this paper, but an extra step is needed to construct provisional up-to-date estimates of a FHLR index.[2] An additional advantage of SW is that it can be estimated using an unbalanced panel (if there are missing data, or with mixed-frequency data) through the use of an iterative procedure that imputes the missing data and re-estimates the model.
The question then arises as to how the estimated factors should be interpreted with regard to the business cycle. If there is only one factor (q=1), then that factor is the only common feature driving the economic series and so has a natural interpretation as a business cycle index. However, that factor can be scaled by a constant (with the factor loadings scaled by the inverse of that constant) without ostensibly changing the model. In other words, the factor is only identified up to multiplication by a scalar constant. While relative changes across time have a natural interpretation, the absolute level of the factor has no defined meaning. If there is more than one factor then the interpretation of the individual factors is less clear. Not only can each factor be arbitrarily scaled by a constant, but the model given by Equation (1) can be represented by alternative linear combinations of the factors. Technically, the factors are only identified up to an orthogonal rotation. It is then not possible to interpret one factor as the business cycle, another as the trade cycle, and so on.
In the Chicago Fed's application of the SW methodology, the implicit assumption is that there is only one factor driving the economic series, and so the CFNAI takes the first factor as being the business cycle index (scaled to have a standard deviation of one). Alternatively, statistical criteria or rules can be used to determine the number of factors that are needed to adequately characterise the panel of data. Two approaches have been used in the literature. Authors using the FHLR methodology have used a given threshold for the marginal explanatory power of each factor included in the model; that is, the increase in the panel R-squared from adding one more factor to explain the panel of data (see Altissimo et al 2001; Forni et al 2000, 2001; and Inklaar et al 2003). So, the marginal explanatory power of the qth factor will exceed the threshold (usually 5 per cent or 10 per cent is used) while the marginal explanatory power of the (q+1)st factor will be less than this threshold. We follow Altissimo et al (2001) in using a 10 per cent threshold. Alternatively, Bai and Ng (2002) have developed information criteria for the static (SW) representation based on the trade-off between the improvement in fit from additional factors and model parsimony. Bai and Ng find that their information criteria often selects too many factors in panels with fewer than 40 series. However, for our dataset we find that their information criterion IC2 puts a reasonable bound on the number of factors, and so we use this criterion to guide the number of factors in the SW estimation.[3]
If more than one factor is important in explaining the data in the panel, the business cycle index can then be constructed as a weighted average of those factors. Authors using the FHLR methodology have used as their weights the factor loadings for GDP, which is included in the panel of data in this methodology. Hence, the business cycle index in this case is the common component of GDP; that part of GDP that can be explained by the factors. Because the data used to derive the factors are mostly log differenced, the index has a natural interpretation as a monthly or quarterly growth rate of the economy (scaled to have mean zero and standard deviation of one). However, while more than one factor may be required to represent the entire panel, this does not imply that all of those factors will be important in explaining GDP. Indeed, in our data the factors other than the first factor often have small weights so the common component and business cycle index closely resemble the first factor. This raises the possibility that some of the higher-order factors might be better thought of as representing some common feature in particular groups of series represented in the panel, rather than factors that are integral to the business cycle.
Footnotes
The quarterly and monthly FHLR indices abstract from volatility with a frequency less than 2π/5 (five quarters) and π/7 (fourteen months) respectively. [1]
The EuroCOIN index, which is calculated using the FHLR method, is initially published on a provisional basis and is revised for several months. [2]
Some of their other information criteria seem to be less robust in our smaller samples, often picking the maximum number of factors the test allowed. [3]