RDP 2005-07: The Australian Business Cycle: A Coincident Indicator Approach Appendix B: Dating Recessions

Christian Gillitzer, Jonathan Kearns and Anthony Richards

October 2005

In this paper, we use the Bry and Boschan (1971) algorithm to date recessions. This algorithm implements NBER-style dating of business cycle peaks and troughs in monthly data. The Gauss code to implement Bry-Boschan for monthly data was obtained from Mark Watson's website <http://www.wws.princeton.edu/~mwatson/publi.html> and was used in Watson (1994). The Bry-Boschan algorithm has been applied to Australian monthly data by Boehm and Moore (1984), Boehm and Summers (1999) and Pagan (1997). We also use a variant of the Bry-Boschan algorithm to date cycles in quarterly series. A quarterly version of the Bry-Boschan algorithm has been used by many authors, including Altissimo et al (2001), Cashin and Ouliaris (2004), Harding and Pagan (2002, 2003, 2005) and Inklaar et al (2003).

The quarterly algorithm, which also serves as an intuitive analogy to the more complex monthly algorithm, is given by the following steps:

Step 1: Local peaks (troughs) in real GDP are found as quarters greater (less) than their neighbouring two quarters either side.
Step 2: Peaks (troughs) are forced to alternate by eliminating the smaller (shallower) of any two consecutive peaks (troughs).
Step 3: A minimum phase length (peak-to-peak or trough-to-trough) of five quarters is enforced. The peak or trough removed is chosen such that the average depth of recessions is greatest after removing that point.
Step 4: Peaks (troughs) that are lower (higher) than previous troughs (peaks) are eliminated by removing that trough-peak (peak-trough) phase.
Step 5: The first and last peaks (troughs) are eliminated if they are not greater (less) than the maximum (minimum) of the points at the ends of the series.

While the FHLR methodology produces a level index, SW does not. We construct a level SW index in an analogous way to FHLR, as shown in Equation (B1):

The growth rate of the level series, gt, is calculated by scaling each observation of the business cycle index, 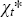Inline Equation, by the parameter σ and adding a mean growth rate μ. The scaling ensures movements of a reasonable magnitude relative to the mean. These adjusted growth rates are cumulated to form an index level. The choice of μ and σ will affect the dating of recessions by determining whether the level of the index falls in any given period. If σ is too small (large) relative to μ the resulting level series will have too few (too many) falls and so too few (too many) recessions. We set μ equal to the mean growth rate of log GDP, and σ equal to the ratio of the standard deviations of four-quarter changes in log GDP relative to four-quarter changes in the coincident indices.[24] This choice produces similar dating to FHLR.

Footnote

FHLR scale the index (which has a standard deviation of one) by the standard deviation of quarterly GDP growth to obtain the level index. While this scaling produces sensible results for FHLR, a similar scaling produces too many recessions for SW because the original SW index is less smooth than FHLR. [24]