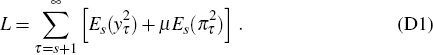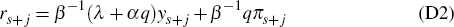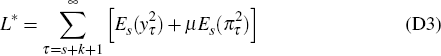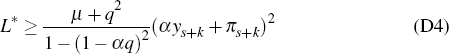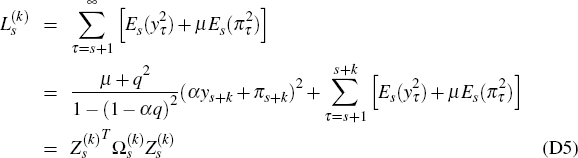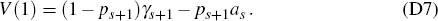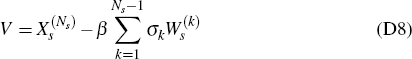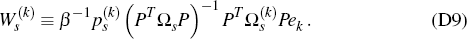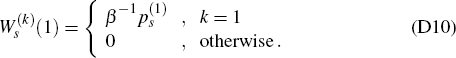RDP 2003-11: How Should Monetary Policy Respond to Asset-Price Bubbles? Appendix D: Some Technical Results Required in Appendix C
November 2003
- Download the Paper 192KB
In this Appendix we set out a number of technical results which we called upon but did not justify in Appendix C, so as not to interrupt the flow of the discussion.
D.1 How the Infinite Loss Horizon is Handled in Appendix C
Recall that the loss function used in the main body of the paper is
In each period s, this combines contributions from each period of the infinite
horizon {s + 1,s + 2,…}. In Appendix C, however, this loss is computed using finite
dimensional matrix algebra involving the matrices  .
.
To understand how this is done, the key observation is that, once a bubble has burst, no further shocks are expected to hit the economy. Then, if the bubble bursts in period s + k, it is well known (see (Ball 1999)) that, to minimise L, the optimal setting for policy, in period s + k and all subsequent periods {s + k + 1, s + k + 2,…}, is given recursively by
where the scalar q is defined by q = (− µα + (µ2 α2 + 4µ)1/2)/2. Note that Equation (7) is just a special case of this general formula, for the case λ = 0.8, α = 0.4, β = 1 and µ = 1.
Using this, it turns out that, for the case of a bubble which bursts in period s + k, it is possible to express the total contribution to the loss function L, from all periods t > s + k, purely in terms of the values of y and π in period s + k. The precise result, the proof of which is available from the authors upon request, is as follows.
Result 1. Consider an activist policy-maker in period s, facing an asset-price bubble which is expected to burst in period s + k, after which no further exogenous shocks are expected to strike the economy. Then the quantity
satisfies that
with equality if and only if policy, in all periods t ≥ s + k, is set according to the recursive rule given by Equation (D2).
It is now easy to see how the use of the infinite horizon loss function, Equation (D1), is
accommodated within the theoretical framework of finite dimensional matrix algebra used in Appendix C. For consider an activist policy-maker in period
s facing an asset-price bubble which has not yet burst. As in Appendix C, let 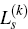 denote the
contingent loss such a policy-maker would expect were the bubble expected to burst in period
s + k. Then, in view of Result 1, we clearly have that in this setting, and
with policy for t ≥ s + k set according to Equation (D2),
denote the
contingent loss such a policy-maker would expect were the bubble expected to burst in period
s + k. Then, in view of Result 1, we clearly have that in this setting, and
with policy for t ≥ s + k set according to Equation (D2),
where  and
and
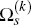 are as
defined in Section C.3 of Appendix
C; and this completes the justification of Equations (C13) and (C14).
are as
defined in Section C.3 of Appendix
C; and this completes the justification of Equations (C13) and (C14).
D.2 A Matrix Algebra Result
In Section C.5 of Appendix C we also invoked the following linear algebra result.
Result 2. For any period s let the matrices P and Ωs, and the vector χs, be as defined in Appendix C. Next, let V denote the Ns × 1 vector
Then there is a simple formula for V(1), the first component of this vector V, in terms of: the bubble's expected growth next period if it survives, γs+1; its current
size 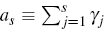 ;
and the probability,
;
and the probability, 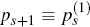 , that it will burst in period s+1, given
that it has not done so by period s. This formula is
, that it will burst in period s+1, given
that it has not done so by period s. This formula is
Proof: The proof of this result is quite lengthy and technical. It is available from the authors upon request. The basic idea, however, is first to establish that we may re-write the vector V in the form
where 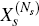 is
as given by Equation (C11), and where, for each k =
1,…,Ns − 1: σk denotes the quantity
is
as given by Equation (C11), and where, for each k =
1,…,Ns − 1: σk denotes the quantity
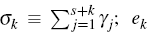 denotes
the Ns × 1 vector (0,…, 0, 1, 0,…,
0)T, the ‘l’ appearing in the kth entry; and
denotes
the Ns × 1 vector (0,…, 0, 1, 0,…,
0)T, the ‘l’ appearing in the kth entry; and
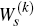 denotes
the vector
denotes
the vector
It then follows directly from Equation (D8) that, to obtain Equation (D7), it will suffice to prove the general formula that, for any k = 1,…, Ns − 1:
Finally, this latter result may be established by: first re-casting the vector quantities 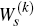 as arising
from a loss minimisation problem, analogous to the way that the vector
V did in Appendix C; and then making a judicious ‘change
of variables’ with respect to which to carry out the loss minimisation – a change of
variables prompted by the structure of the Ball model.[27] QED
as arising
from a loss minimisation problem, analogous to the way that the vector
V did in Appendix C; and then making a judicious ‘change
of variables’ with respect to which to carry out the loss minimisation – a change of
variables prompted by the structure of the Ball model.[27] QED
Footnote
Specifically, recall that in the Ball model changes in interest rates flow through to
inflation (via output) with a lag of two periods. Hence,
the following two options are readily seen to be equivalent: on the one hand,
determining an optimum profile for interest rates, rt, in periods t = s, s + 1,…, 13,
so as to minimise a given loss function; and on the other, seeking instead an optimum
profile for inflation, πt, in periods t =
s + 2, s + 3,…, 15, so as to minimise this loss, and then
recursively back-solving for the corresponding implied profile for 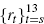 .
It is this latter approach which we employ.
[27]
.
It is this latter approach which we employ.
[27]