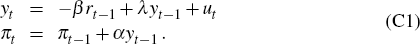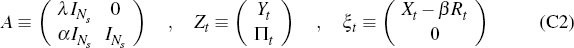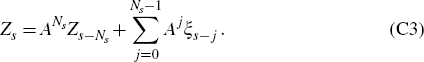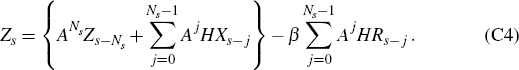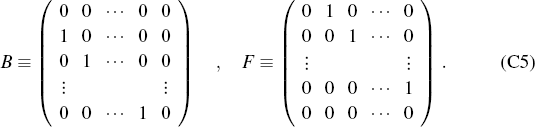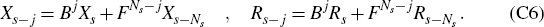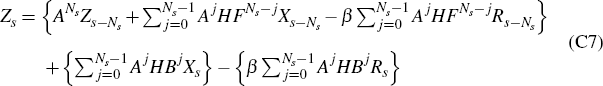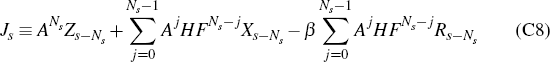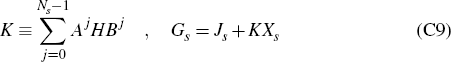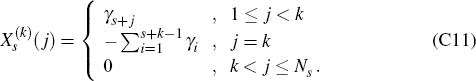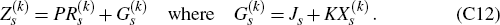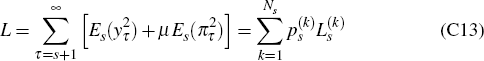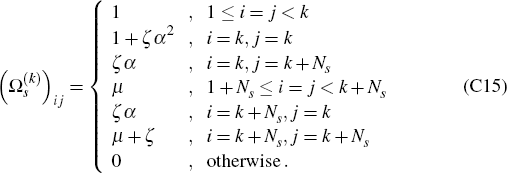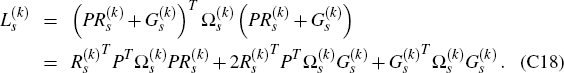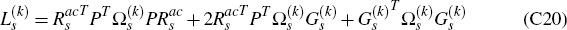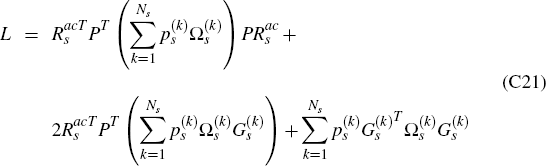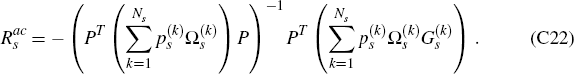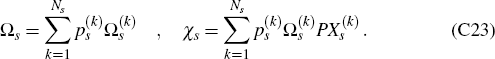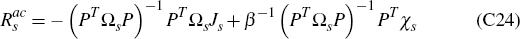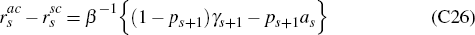RDP 2003-11: How Should Monetary Policy Respond to Asset-Price Bubbles? Appendix C: Analytic Solution of the Optimal Policy Problem

In Section 3 we compared the recommendations of activist and sceptical policymakers, when confronting various types of asset-price bubbles. For asset-price bubbles which are not influenced by policy, it is possible to derive an analytic formula for the difference between the recommendations of these two types of policy-makers. In this Appendix we outline this derivation in detail. The working is somewhat complicated owing to the contingent nature of the optimal policy problem facing an activist policy-maker in this setting.

The derivation proceeds in several stages. We first describe, in Section C.1, the contingent optimal policy problem facing an activist policy-maker, confronted by an asset-price bubble whose stochastic properties she cannot affect. Before attempting to treat this contingent problem, however, we then derive, in Section C.2, the analytic solution to the optimal policy problem facing an activist policy-maker in our Ball-style economy, when confronting a known set of future exogenous shocks to output.

Next, in Section C.3, we discuss how the optimal policy problem set out and solved in Section C.2 needs to be modified to handle the case of an exogenous asset-price bubble of the form treated in the main body of the paper – where an activist faces, not a known set of future exogenous shocks to output, but rather an array of possible different sets of future shocks, depending upon how the bubble develops in subsequent periods. This more general contingent optimal policy problem is then solved explicitly, in matrix terms, in Section C.4.

Finally, we then use this general solution to study the difference between the contingent optimal policy recommendations of activist and sceptical policymakers confronting an asset-price bubble. As in Section 3, we assume throughout that policy is ultimately set in each period by the sceptic.^[22]

C.1 Nature of the Problem for an Activist Policy-maker

Consider an activist policy-maker, in the economy described by Equations (4) and (5) of Section 2, facing an asset-price bubble developing according to Equation (3), and seeking to minimise the loss function given by Equation (6). As in Section 3, we assume that the bubble will burst with certainty in year 14, if it has not already done so. We also assume it to be unaffected by the actions of policy-makers.^[23]

For each period s = 0,1,…, 13 we wish to derive the analytic solution to the policy-maker's problem of determining the optimal current policy response to this situation. Note that, since the bubble will definitely have burst by period 14 (and is assumed not to re-form thereafter), we already know what an activist will recommend for policy in periods s = 14,15,…, namely that policy simply be given by Equation (7).

In formulating the optimal policy problem facing an activist policy-maker in each period s = 0,1,…, 13, it is crucial to appreciate that we seek here the contingent policy recommendation which such a policy-maker would make. In other words, we seek the recommendation they would make on the understanding that, whenever the bubble does ultimately burst, policy may be switched from then on to a profile better suited to an economy no longer experiencing an asset-price bubble.^[24] Specifically, for each period s = 0,1,…, 13, we therefore seek the optimal (14 − s)-component vector, 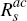, of contingent policy recommendations which an activist would, in period s, wish to see enacted in periods {s, s + 1,…, 13} unless the bubble bursts, say in period s + k, in which case policy, for periods {s + k,s + k + 1,… ,13}, would then switch to being set by Equation (7). The activist's actual policy recommendation for period 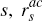, is then just the first component of this vector .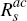

C.2 A Convenient Matrix Form for the Solution of the Ball Model

We begin by writing the Ball model in a slightly more general form than that used in the main body of the paper, viz:

Here we have included a term for a general exogenous shock in period t, u_t, in the output gap equation. Writing this equation in this way helps to simplify the subsequent discussion – even though we ultimately wish to focus on the case where the shocks {u_t} arise from a bubble via u_t ≡ Δα_t, as in Equation (4).

Now consider any fixed period s ∈ {0,1,…, 13}. To determine an activist policy-maker's policy recommendation for period 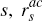, we need first to establish a suitable matrix form for the solution of the Ball model, Equation (C1), over the horizon {s + 1,s + 2,…, 14}, in the event that: the economy is expected to be struck by some given set of exogenous shocks {u_s+1,…,u₁₄}; and that policy in periods {s,s + 1,…,13} is to be set according to some given path {r_s, r_s+l,…, r₁₃}. By solution of the Ball model we mean here determination of the profiles for output and inflation over the horizon {s + 1, s + 2,…, 14}.

To this end, set N_s ≡ 14 − s. Then, for any t ≤ s, let y_t, Π_t, R_t and X_t denote the N_s × 1 vectors 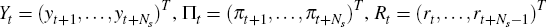and 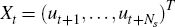. Also, let A denote the 2N_s × 2N_s matrix, and Z_t and ξ_t the 2N_S × 1 vectors, given by

where 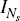denotes the N_s × N_s identity matrix. Finally, let H denote the 2N_s × N_s matrix given by 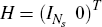, so that ξ_t = H(X_t − βR_t).

Then, for any t ≤ s we have that Ball's model for the N_s-period horizon {t + 1,…,t+N_s} may be written compactly in matrix form as the relationship Z_t = AZ_t-1 + ξ,_t. By simple iteration (and writing A⁰ for 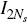) it then follows that

This represents an expression for Z_s in terms of:

• future exogenous shocks 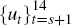, and current and future policy settings 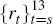, which enter through the vectors 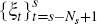; together with
• initial conditions for the endogenous variables y_t and π_t, as captured by the vector .

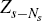Moreover, using that ξ_t = H(X_t − βR_t), it follows immediately that we may write

To proceed further, now introduce the ‘backward’ and ‘forward’ shift operators, B and F, given in matrix form by the N_s × N_s matrices

Then observe that, for any j = 0,…, N_{S − 1}, we may write

Hence we may rewrite Equation (C4) in the form

where the first bracket of terms here represents purely ‘historical’ effects (that is, the influence of initial conditions); the second captures the impact of expected exogenous shocks over the horizon under consideration; and the third reflects the influence of monetary policy settings over this same horizon.

For any given initial conditions, given set of policy decisions {r_s, … , r₁₃}, and given set of exogenous shocks {u_s+1,…,u₁₄}, Equation (C7) represents the general solution to the Ball model, over the horizon {s + 1, … , 14}, expressed in suitable matrix form. Moreover, if we now introduce the notation

and then set

then we may write Equation (C7) more compactly as the formula

where P is the 2N_S × N_s matrix defined by P ≡ −βK.

C.3 Mathematical Formulation of the Problem Facing an Activist Policy-maker in Period s

We now wish to formulate precisely the optimal policy problem facing an activist policy-maker in period s, trying to determine the optimal policy vector, 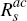, of contingent policy settings to recommend for periods {s,s + 1,…, 13}. To do this, it is necessary first to introduce yet some further notation.

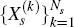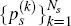First, let denote the N_s different possible N_s × 1 vectors of exogenous shocks which an activist policy-maker might expect to hit the economy in periods {s + 1, s + 2,…, 14}, depending (respectively) on whether the bubble bursts in period s + 1, period s + 2, …, or period 14. Also, let denote the associated probabilities with which each of these possible shock profiles is expected to occur, as at period s.^[25] Note that, in view of Equation (3) of the main paper for the way an asset-price bubble evolves, the vectors 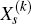are given explicitly, for each k = 1,… N_S, by the formula

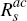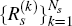Next, for any given choice of vector of contingent policy recommendations by the activist policy-maker, , let denote the corresponding set of policy paths which would actually be followed by the activist over the horizon {s, s + 1,…, 13}, depending upon when the bubble actually bursts. Thus, for each k, 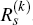is an N_s × 1 vector whose first k entries would be the same as those of 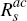, but whose remaining entries would then be as determined by Equation (7) (see also Equation (D2) of Appendix D).

Finally, let 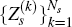denote the corresponding 2N_S × 1 vectors of outcomes for output and inflation over the horizon {s + 1,…, 14} which would occur in the event that the bubble bursts (respectively) in period s + 1, period s + 2, …, or period 14. Thus, 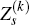denotes the vector of outcomes for output and inflation which would occur in the event that 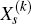describes the exogenous shocks striking the economy over this horizon, and that policy is given by the vector 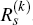. Note that, by Equation (C10), we will then have simply, for each k:

Armed with this notation, we can now formulate precisely the optimal policy problem facing an activist policy-maker in period s. For now, invoking also Result 1 of Appendix D, it is clear that, for any given choice of contingent policy recommendations 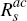over the horizon {s,s + 1,…, 13}, the corresponding loss expected by an activist policy-maker would be

where

and where the 2N_S × 2N_S matrices 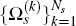are given by

Here, ξ = (µ + q²)/(1 − (1 − αq)²) is a scalar which arises from the working in Appendix D, expressed in terms of another scalar, q = (−µα + (µ² α² + 4µ)^1/2)/2.

Therefore, finally, in any period s = 0,1,…, 13, the activist policy-maker's task of finding the optimal contingent set of policy settings to recommend over the horizon {s, s + 1,…, 13} may be expressed succinctly as: find the policy vector 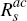which minimises

where each 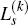is as given by Equation (C14), subject to the condition that

for each k (where the quantities P, 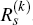and 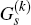are as defined earlier).

C.4 Solution of the Problem Facing an Activist Policy-maker

To solve the optimal policy problem just posed, observe first that, for each k = 1,…, N_s, by putting Equation (C17) into Equation (C14) and expanding we may write

To simplify this expression we next exploit the fact that, for each k, the vectors 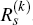and 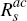have the same first k components. One implication of this is that, for each k, we have the identity

Hence, noting also that 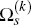is a symmetric matrix, we may rewrite Equation (C18) as

for each k = 1,…, N_s. Then, in view of Equation (C16), it follows that

and the activist policy-maker's task is to choose 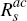so as to minimise this quantity. Yet the solution to this optimisation problem is well-known to be given by

Finally, this expression may be simplified slightly if we introduce the notation

Then, using the definitions of P and 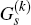, it follows from Equation (C22) that

which expresses 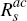as a function of the matrices P and Ω_s, the vectors J_s and χ_s, and the parameter β.

Note that, importantly, the vector J_s in Equation (C24) is a function purely of the vectors 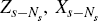and 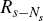. Hence, the solution vector, 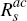, given by Equation (C24) may be viewed as consisting of two parts: a part reflecting the past set of economic outcomes, policy actions and exogenous shocks which have occurred up to period s, captured in the first term on the right hand side of Equation (C24); and a part reflecting the future exogenous shocks which the policy-maker expects to buffet the economy over the policy horizon {s + 1, s + 2,…, 14}, as captured by the second right hand side term of Equation (C24).

C.5 The Difference between the Recommendations of Activists and Sceptics

Fortunately, we are really only concerned with the first component of the vector 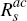, since this is the policy recommendation which the activist must actually make for the current quarter. Denote this first component by 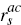, and write 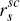for the corresponding policy recommendation of a sceptic for the current quarter. Then it turns out that, using a matrix algebra result set out in Appendix D, we can derive from Equation (C24) a simple analytical expression for the quantity (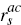 − 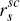), the difference between the recommendations in each quarter of activist and sceptical policy-makers.

In more detail, one way to think about a sceptic is as an activist who thinks that all the vectors 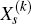are zero, and so expects no future exogenous shocks to output. It follows that the policy recommendation of a sceptic, in each period, is also given by the first component of a vector of the form given by Equation (C24) – except with the quantity ‘χ_s’ treated as being zero, so that the second term in this formula vanishes. Hence, 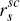is given, in each period s, by the first component of the vector (P^T Ω_SP)⁻¹ P^T Ω_SJ_S, where the vector J_s is the same as for an activist policy-maker.^[26]

This, however, then means that the difference between the policy recommendations of an activist and a sceptic in each period s will be given simply by the first component of the vector

Finally, this then turns out to yield a simple formula for this difference between the policy recommendations of activist and sceptical policy-makers, in view of Result 2 in Appendix D. We obtain that this difference is independent of the model parameters α and λ, and of the loss function parameter µ. Explicitly it depends, in each period s, only upon the bubble's expected growth next period if it survives, γ_s+1, its current size 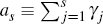, and the probability, 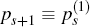, that it will burst in period s + 1, given that it has not done so by period s:

which is precisely the formula noted in Footnote 6 in Section 3.

Footnotes

Note, however, that for the working which follows it does not in fact matter upon what basis policy is eventually set in each period. All that matters is that both activist and sceptical policy-makers face an economy in the same state in each year, when devising their recommendations on the optimal stance of monetary policy. [22]

This assumption applies throughout this Appendix. Analytical treatment of bubbles whose development is affected by the actions of policy-makers turns out to be far more difficult than that of bubbles which are unaffected by policy. Moreover, for bubbles which are influenced by policy, analytical treatment does not yield a simple, closed formula for the difference between the policy recommendations of activist and sceptical policy-makers. This contrasts with the results obtained in this Appendix for bubbles which are uninfluenced by policy. [23]

See Footnote 6 regarding the contingent nature of the policy problem facing an activist policy-maker in the current setting. [24]

Note that these probabilities are not the same as the probabilities, {p_t}, referred to in the main body of the paper. Recall that, for each t, p_t+i denotes the conditional probability that the bubble will burst in period t+l, given that it has not done so by period t. For any period s, the two sets of probabilities are thus clearly related by the formulae: 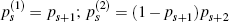; 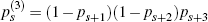and so on. [25]

Here we are using that our activist and sceptical policy-makers face an economy in the same state in each period s, which ensures that the vector J_s is the same for both types of policymakers. [26]