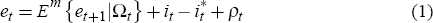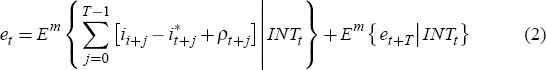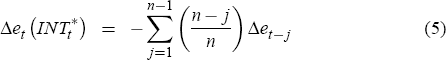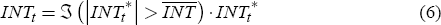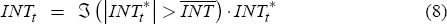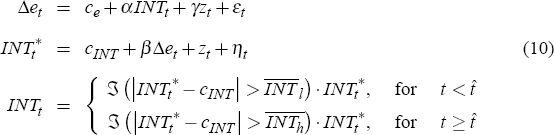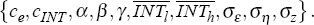RDP 2003-04: Identifying the Efficacy of Central Bank Interventions: Evidence from Australia 4. Identification of the Effectiveness of Intervention

In this section we use a simple model of central bank intervention to demonstrate how intervention and the exchange rate interact and the technique we use to solve the identification problem.

A useful starting point to consider the effects of intervention on the exchange rate is a generalised version of uncovered interest parity (UIP)

where E^m {·} is the markets' expectation operator, e_t is the exchange rate (value of domestic currency), ρ_t represents possible predictable deviations from UIP (risk premia), and Ω_t is the time t information set, which includes contemporaneous and past interventions, 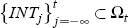. Substituting forward this relationship, and suppressing other elements of the information set, the exchange rate is

where e_t+T is the exchange rate at some distant time t+T. A sterilised intervention to support the domestic currency will increase investors' holdings of foreign bonds and decrease their holdings of domestic bonds. If domestic and foreign bonds are imperfect substitutes investors will require a risk premium (ρ > 0) to increase their relative holdings of foreign bonds. Through this portfolio balance channel, for some long-run value for the exchange rate, e_t+T, it can be seen in Equation (2) that intervention appreciates the exchange rate.

The signalling channel describes the use of intervention by the central bank to disseminate inside information about exchange rate fundamentals, either interest rates or the long-run value of the exchange rate. Intervention is supposedly a credible communication mechanism because it rebalances the central bank's portfolio in such a way that it profits from resulting changes in the exchange rate and its fundamentals. The central bank will profit from future increases in domestic interest rates if its portfolio has been rebalanced through intervention to support the currency. Intervention can then credibly communicate the bank's intended path for monetary policy, increasing E {i_t+j|INT_t}. Alternatively, the central bank may use intervention to communicate its view of the ‘long-run’ value of the exchange rate, so affecting the markets' expectations E^m {e_t+T}. Since the exchange rate will respond to current bond supplies and current news, both the portfolio balance and signalling channels indicate the exchange rate is a function of contemporaneous intervention, e_t = e_t (INT_t).

As noted earlier, central banks typically state that they intervene to slow or correct excessive trends in the exchange rate and to calm disorderly markets. Indeed, the Governor of the RBA states that the RBA has used intervention in ‘circumstances where market imperfections are resulting in overshooting’ and that ‘intervention can play a useful role in limiting extreme movements in the exchange rate’ (Macfarlane 1998). Since the RBA sterilises interventions, and is acknowledged to allow the Australian dollar to float quite freely, it seems reasonable to assume that intervention is not used as a separate policy tool with independent goals. Rather, intervention is focused on exchange rate outcomes. A simple representation of this policy, as used in Almekinders and Eijffinger (1996), is that the central bank's preferred level of intervention, or shadow intervention, INT^*, would minimise squared deviations of the exchange rate from a moving target.

Given the central bank is allowing the exchange rate to float, but doesn't want it to move ‘too quickly’, the target is taken to be a moving average of past values of the exchange rate, 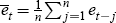. The optimal level of intervention will then by given by

However, central banks do not intervene on every day, and very small interventions are extremely rare. Presumably there are some costs to intervention, possibly because the strength of signals is reduced if they are used too frequently. As a result the central bank only intervenes if the loss function would exceed some benchmark, or equivalently if the shadow intervention exceeds a given threshold, otherwise remaining absent from the market. Actual intervention can then be represented as

where 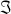(·) is the indicator function. Equations (2), (5) and (6) constitute a system that determines the exchange rate and intervention.

4.1 Set-up of the Estimation System

We generalise the previous framework to include unobservable variables that affect the exchange rate and the central bank's decision for intervention. The reason behind this extension is that we believe that there are factors that are unobservable at daily frequencies that have impact on both variables, such as liquidity shocks, macro shocks, etc. The model used is:

where Δe_t is the observed exchange rate return at date t (a positive value is an appreciation), INT_t is the observed intervention (positive values are purchases of the domestic currency), and 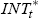is a shadow intervention. The estimation procedure includes constants and potentially lags, but this simple version is sufficient to demonstrate the endogeneity problem.

Equation (7) is the reaction of the exchange rate to the central bank intervention. We assume that the exchange rate is affected by two types of shocks: ε_t which is a pure idiosyncratic shock to the exchange rate, which we assume has no direct impact on the intervention decision; and a common shock (z_t) which is assumed to move both the exchange rate and the central bank intervention decision. We explore the interpretation of these shocks below.

Equation (8) is the decision of the central bank to intervene or not. We assume that this decision is made entirely based on the shadow intervention. In other words, if the required intervention is large (larger in absolute terms than some threshold 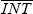), then the central bank participates in the market, otherwise it remains absent. Observe that implicitly we assume that if the shadow intervention is larger than the threshold then the central bank intervenes, and its intervention is exactly the shadow one.

Equation (9) determines the shadow intervention. We assume that it is affected by the movements in the exchange rate, by the aggregate or common shock, and by some idiosyncratic shock reflecting innovations to exchange rate policy. If the central bank aims to offset changes in the exchange rate, i.e. lean against the wind, then β will be negative. Equations (8) and (9) together constitute the central bank's reaction function; where the former reflects the decision to intervene, and the later one determines the quantity or size of intervention.

The policy shock (η_t) is interpreted as innovations in the exchange rate target that are independent of the nominal exchange rate shocks (ε_t) and the common shock (z_t). The idea is to separate idiosyncratic shocks to policy (such as trades on behalf of the government or unwinding of positions) and to the exchange rate (for example, economic fundamentals) from those shocks that we might expect to affect both variables (such as herding, liquidity, or shocks to the exchange rate during periods of high conditional volatility). These common shocks will affect how intervention takes place, and the exchange rate at the same time. We assume that these shocks are i.i.d., with mean zero and variances 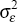, , 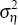and 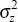. For simplicity in the exposition we have assumed that all the variables have zero mean, but in the empirical implementation it is important to include constants to account for non-zero means.

Finally, the parameter of interest is α. If central bank intervention is effective, then purchases of the domestic currency will appreciate the currency and so α will be positive.

The intuition for this model is that the central bank leans against the wind, so β < 0, either to slow deviations from trend, or to calm volatile markets. Small changes are tolerable and so the central bank does not bother intervening. On the other hand, if exchange rate returns would otherwise be large, larger interventions would be required to counteract these and will cause the central bank to enter the market. The shadow intervention 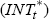summarises the expected intervention if the central bank were to trade continuously in the foreign exchange rate market.

This simple framework captures the two sources of simultaneity that exist in the data. The first one is the endogenous decision of participation. The second one is the size of the intervention and the change in the exchange rate once the decision of participation has been made. While the first source of bias has been widely acknowledged in the literature, the second has received very little attention. This is understandable. Finding instruments for the first one is hard, but some might be available. For the second one, this is much more difficult.

In this model there does not exist an instrument that can be used to solve the problem of simultaneous equations. More importantly, this bias is likely to be negative, pushing the estimate of α in Equation (7) downward, possibly even negative, explaining most of the results found in the data.

It is important to mention that there are several aspects of central bank intervention that have been oversimplified in this model. First, there is no distinction between public and secret interventions. As was mentioned before, this has received considerable attention in the literature. In this paper we focus on the estimation problem. Second, we do not attempt to distinguish between sterilised and unsterilised interventions as the RBA states that all of its interventions are sterilised.

4.2 Identification through Changes in Intervention Policy

The problem of identification is easily shown by counting the number of unknowns and the number of series we can measure in the model. Under the assumption that we only observe the exchange rate, the size of the intervention, and its timing, then, aside from the means, we can compute only five moments from the data: the probability (or frequency) of intervention; the variance of the exchange rate when there is no intervention; and the covariance matrix when an intervention has taken place. 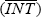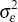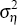However, in the model there are seven unknown coefficients that explain the behaviour of such variables: the parameters of interest (α, β, and γ), the threshold of intervention and the three variances(, , and 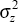).^[13]

The standard procedures in the literature use the following assumptions. First, that there are good instruments for the participation decision. Second, that either β = 0 or α = 0 (exclusion restrictions). And third, that the instrument is correlated with η_t but not with z_t. This set of assumptions seems rather strong. Central banks no doubt intervene based on their most recent information set, which includes the change in the exchange rate during the day. Further, the fact that central banks know they have market power, which is the whole rationale for intervening in the first place, collides with the assumption that β = 0. Central banks should be, and indeed are, strategic in their interventions. The alternative identification assumption that α = 0 is similarly problematic in that it implies that central bank interventions don't have any effect on the day during which they are conducted. This contradicts significant circumstantial evidence.

The main contribution of this paper is to relax these set of assumptions and use an alternative identification method that can deal with some of the econometric issues at hand. Obviously, we depend on another set of assumptions. We think those are weaker, in the sense that most of them are already imposed in the standard literature. But this is certainly the first pass at the problem using these alternative methods and further research should extend the present procedure. We discuss the caveats in detail at the end.

Our identification procedure is quite simple; in September 1991, the RBA changed its foreign exchange rate intervention policy. Following the change, the RBA all but ceased to conduct small interventions but continued to undertake larger interventions as before the change. In the model this would be summarised by a shift in 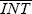. Effectively, this means that there are two regimes. Under the assumption that the parameters and the variance of the shocks remain the same across both regimes, we have only eight unknowns (one more than before because we have two thresholds) but at least ten moments in the data.

Specifically, the basic model we estimate is the following:

Note that in this setup we allow for constants in the mean equations and below we extend the model to also include lags.^[14]

We estimate this model with, and without, lags and present both results. When the model is estimated without lags, there are 10 parameters of interest:

To estimate the model with lags it is necessary to use moments that account for the behaviour of the exchange rate and intervention across days. For consistency, we use the same set of moments to estimate both the models with and without lags. We compute the following moments in each of the regimes: the proportion of days with intervention; the variance of the exchange rate on days with no intervention; and, the variance-covariance matrix on days with intervention. Furthermore, we compute the mean exchange rate return; the mean intervention; the moments related to the serial correlation of the exchange rate; and the probability of consecutive interventions.^[15] In total there are 24 moments, greater than the number of parameters, leaving our system over-identified.

We use simulated GMM to estimate the model. The general idea of this procedure can be easily understood by analysing how other techniques estimate the coefficients. For example, when we use Maximum Likelihood (ML) the goal is to estimate the parameters using the mean and the variances. GMM extends that procedure and uses other moments. Simulated GMM is a further generalisation, in which we choose different moments and characteristics from the data, and ‘create’ our own data using our auxiliary model to match those ‘moments’. Indeed, all three techniques use auxiliary models for their estimation. On the one hand, in ML we use multinomial distributions, described only by means and variances. On the other hand, simulated GMM creates its own data within a well-specified model to produce the statistics that we are interested in matching from the population.

In summary, the procedure is as follows: First, we create random draws of 20000 observations for three uncorrelated shocks with unitary variance. The same set of shock variables are retained for the entire estimation procedure. Second, we simulate the model given some initial conditions and calculate the moments of these simulated data. Third, we compute the ‘distance’ – the sum of the absolute differences – between the population and simulated moments. Finally, we iterate this procedure to search for the coefficients that minimise this distance. Because the probabilities of intervention are two orders of magnitude larger than the variances and covariances we multiply both the intervention and exchange rate data by 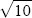so that the probabilities and variances and covariances are of equivalent magnitudes. This transformation is used to simplify the maximisation procedure.

To calculate the standard errors of the estimates we use the asymptotic distribution of the sample moments. Using the data, we bootstrap the exchange rate, intervention, and probabilities of interventions to produce a sequence of moments (100 of them). Then we estimate the coefficients for each draw of the moments, computing the distribution of our coefficients. Because it is likely that the data are serially correlated, the bootstrap takes this into account.

Footnotes

The estimation of means adds the same number of equations and unknowns to the system, thus, the problem of under-identification remains the same. [13]

The lag structure takes into account that the exchange rate can only depend on observable variables. Thus, the lag of intervention used is INT_t−1 and not 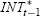. However, for the shadow intervention equation we allow it to depend on the lag shadow realisation. [14]

We have run the simulation also including other moments such as the probability of two positive interventions, and the correlation in the quantities of two consecutive interventions. The results were not sensitive to these changes. [15]