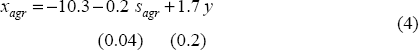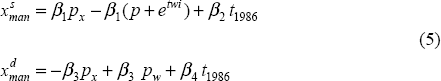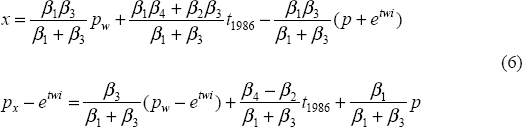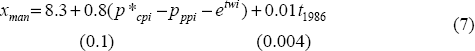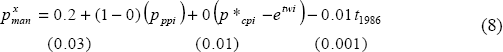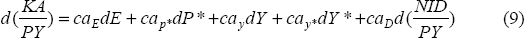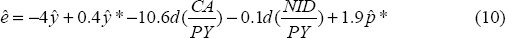RDP 2003-03: Australia's Medium-Run Exchange Rate: A Macroeconomic Balance Approach 3. Empirical Estimates
March 2003
- Download the Paper 218KB
This section presents empirical estimates of the parameters required to implement the approach set out in Section 2.2. As discussed there, we proceed directly to Step 2, since we evaluate the macroeconomic balance exchange rate as a function of the target capital account. In Section 3.1 we discuss the underlying current account equation. The coefficients of this equation are functions of trade elasticities, which are estimated in Section 3.2. In Section 3.3 we evaluate Step 3 and derive estimates of exchange rate equilibria under a range of alternative assumptions and time periods. Confidence intervals (Section 3.4) illustrate the degree of uncertainty around these estimates.
3.1 The Underlying Current Account
Our first task is to model the underlying current account. We are interested in the answer to two questions. How does the current account change if output moves to potential? And how does the current account change if the exchange rate changes? We are primarily interested in the long-run impact of these variables; that is, once pass-through is complete.
Following Equation (2), we model the Australian current account as the sum of net foreign income, the trade balance, and net transfers. Let us consider each component in turn. Net foreign income accounts for a large part of Australia's current account deficit (on average, 80 per cent in 1997–2001). Net foreign income consists mainly of net investment income, and therefore we ignore net compensation from foreign employment in our model. Net investment income is the interest income from net foreign asset holdings, which in Australia's case are net foreign liabilities. The main effects of exchange rate changes are valuation effects, which only apply to the share of net interest income that is denominated in foreign currency. We assume that there is no effect from closing the output gap on this term (for more details see Appendix B). Net investment income, while being an important part of Australia's current account, is relatively stable through time.
Most of the movement in the current account stems from changes in the trade balance. Because it is strongly influenced by movements in output and the exchange rate, our econometric analysis focuses on this component. For the trade balance we use a disaggregated model of trade, described in more detail in Section 3.2. Finally, net transfers, which account for only a small fraction of the current account, are modelled using a simple time trend. They are therefore assumed to be independent of changes in the exchange rate or in the output gap.
Once we have estimated the trend trade balance we can obtain the empirical equivalent to Equation (3), the underlying current account, which can then be solved for the exchange rate, conditional on the assumed target capital account.
3.2 Empirical Estimates of Trade Elasticities
We estimate the trade balance for Australia using data up to 2001:Q4. The starting points of the series vary from 1971:Q3–1984:Q3 (see Appendix A for more details on the data). Since the methodology is cast in terms of medium-run relationships, the time series properties of the data must be taken into account. We tested the data and found that they are non-stationary over the sample period (details in Appendix C). A cointegration framework is therefore the appropriate methodology.[5]
Particular care is taken to gauge the effects of the exchange rate on prices and volumes. This requires some clarification of the choice of the exchange rate. In principle, the macroeconomic balance approach identifies the real exchange rate and therefore most studies solve for a real exchange rate equilibrium level. The implied nominal exchange rate can then be calculated for given relative prices in a specific period. With our disaggregated approach to modelling the trade balance, we have multiple real exchange rates and therefore solve directly for the nominal effective exchange rate (the TWI, abbreviated with Etwi) instead.[6]
In principle, one could estimate the impact of changes in the exchange rate and output on the trade balance using an aggregate model, for instance, with one equation for aggregate exports and another for aggregate imports. However, we found it difficult to uncover a statistically significant exchange rate effect for these aggregate equations. Where we did, the coefficient was often unstable or had the ‘wrong’ sign. We therefore opted to use a disaggregated approach, following much of the existing literature on trade equations for Australia. We model goods and services separately for both exports and imports. Moreover, because we find it very difficult to model aggregate goods exports, we break this particular category up into the three subcategories of rural goods' exports, resource goods' exports and manufactured goods' exports. For each category there is potentially a volume and a price equation.
Trade equations are best thought of as arising from a demand and supply system. Therefore, there are simultaneity issues that are relevant for our estimation. Most of our estimated equations assume that Australia is a price maker or price taker, and thus eliminate either demand or supply from the system. Table 1 shows how this is applied to the different trade components. Clearly, there is no price equation to estimate when we assume either polar assumption of price making or price taking.[7]
| Aggregate | Price taker or price maker? |
Estimated relationship |
Price or volume estimated? |
|---|---|---|---|
| Exports | |||
| Agricultural | Price taker | Local supply | Volume |
| Resource | Price taker | Local supply | Volume |
| Manufactured | – | Reduced form | Price and volume |
| Services | Price maker | World demand | Volume |
| Imports | |||
| Goods | Price taker | Local demand | Volume |
| Services | – | Local demand and price | Price and volume |
In what remains of this section, we illustrate our estimation techniques using the first two trade components in Table 1 – agricultural and manufactured exports. For agriculture, we assume that Australian producers are price takers. This allows us to identify the supply curve since the demand curve is given by the world price. Similar simplifying assumptions of price taking or price making are used for resource exports, service exports and goods imports. For manufactures, we avoid the simplifying assumption and estimate the reduced form of a price and volume system. For service imports, we estimate both a price and a volume equation, but they are not explicitly derived from a reduced form.[8]
3.2.1 Agriculture
We model the supply curve using real GDP to account for capacity constraints and subsidies to capture any supply shocks. Under the maintained hypothesis that Australia is a price taker, world output has no direct effect on export volumes.[9]
We estimate the long-run relationship using a VECM with four lags (Equation (4)). For illustration purposes we only report the long-run coefficients. The standard deviations are below the point estimates of the coefficients in brackets. Lower case variables are in logs.
where xagr denotes the volume of agricultural exports, sagr are agricultural subsidies not included in gross value of production, and y is Australian real GDP. The results are illustrated in Figure 2.
3.2.2 Manufactures
For manufactures, we do not want to impose price taking or price making a priori. We therefore set up a demand and supply equation for manufactures in the world market and obtain the reduced forms. Variables are natural logarithms and constants are ignored for the exposition. Prices are in US$, all coefficients are positive, and zero price homogeneity is imposed.
The supply equation says that Australian producers may sell their goods onto the world market for a US$ price of px or sell it locally for a price (expressed in US$) of p + etwi. On the demand side, overseas consumers can buy the Australian good for px, or a world good (a consumption substitute) for pw. The pronumeral t1986 represents other supply and demand influences. Following Menzies (1994), the supply effects are micro reforms and tariff reductions made effective by the large mid 1980s depreciation. The demand effects are the increased market penetration of Australian firms as the ‘vanguard’ of new exporters made their presence felt. All these influences are modelled by a broken trend, starting in 1986. The system given by Equation (5) can be solved to give the following reduced forms.
An inspection of the system shows that the right-hand side of the volume equation can be written as a relative price and as a broken trend (representing both supply and demand influences). The sum of the price coefficients in the price equation is unity.
We estimate the long-run relationship using a VECM with eight lags:
where xman is the volume of manufactured exports, 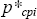 are world consumer prices, etwi is the effective exchange rate (increase is
an appreciation), pppi are domestic producer prices, and
t1986 is a broken trend starting in 1986. The results of the volume equation
in Equation (7) are illustrated in Figure 3.
are world consumer prices, etwi is the effective exchange rate (increase is
an appreciation), pppi are domestic producer prices, and
t1986 is a broken trend starting in 1986. The results of the volume equation
in Equation (7) are illustrated in Figure 3.
We estimate the reduced form expression for the price of manufactured exports, with the restriction imposed that the price coefficients sum to unity, and are non-negative. We used Non-linear Least Squares (NLS) to impose the latter restriction:
where  is
the Australian price of manufactured exports. The results are illustrated in Figure 4.
is
the Australian price of manufactured exports. The results are illustrated in Figure 4.
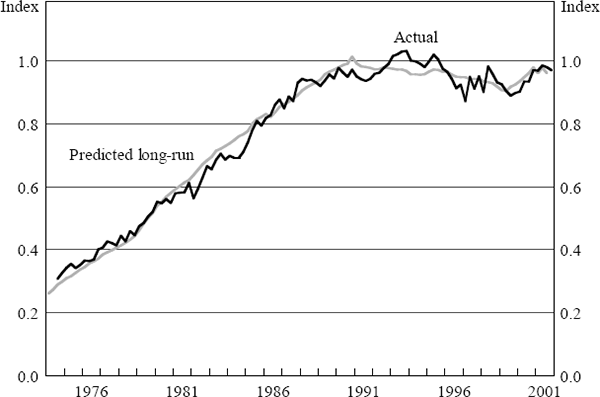
Appendix B gives the remaining trade equation estimates, plus the results for our model for income and transfers.
Overall, we are confident in our estimates of goods imports and service exports. This is not surprising since goods imports have been successfully modelled in other studies (e.g., Wilkinson (1992)). The equations for manufacturing, agriculture, and resource exports are econometrically sound, but the results are sensitive to changes in the specifications. The model for service imports, however, is less satisfactory, since we have to impose restrictions in order to obtain economically sensible results.
One of our aims is to estimate the exchange rate effect on the trade equations. We find a significant effect on the volumes of manufacturing and services exports, on the volumes of goods and services imports, and on the price of manufacturing exports. The assumption of price taking, which implies an exchange rate effect, is accepted for the prices of agriculture exports, resource exports, and goods imports. The exchange rate effect on service import prices, however, is imposed.
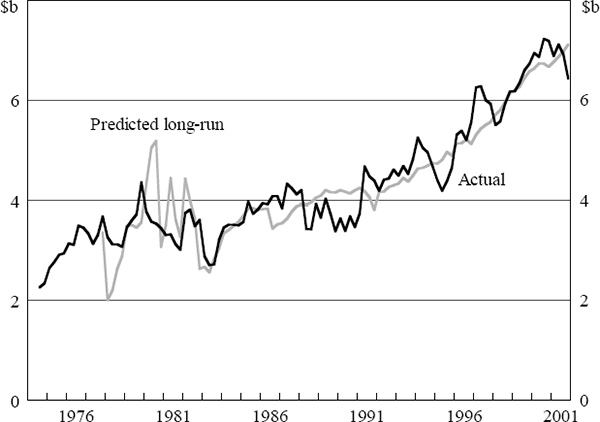
We can now add the different components of the current account. Figure 5 shows how the predicted values from our current account model compare against the actual values. We should bear in mind that our estimates are long-run estimates only, while the actual series also contains short-run dynamics, which will be poorly explained by our model. The model tracks the medium-run trends reasonably well in the early and late 1990s, but appears to be more problematic in the mid 1990s.
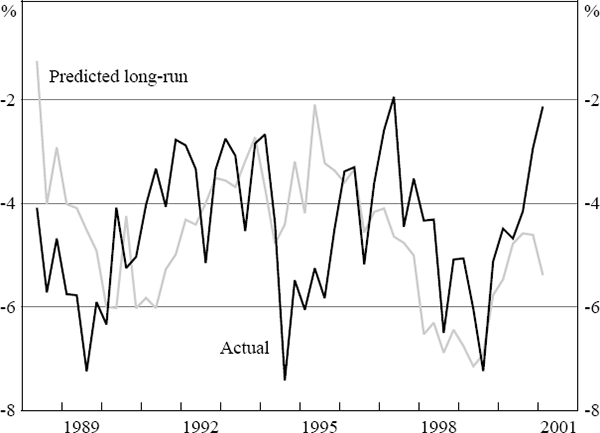
Armed with the required elasticities, it is now possible to calculate the coefficients in Equation (3). In order to calculate the underlying current account for a specific period, we have to set the output gap to zero and we have to set the exogenous variables to their values in that period.[10] The estimated underlying current account (and thus the estimated value for the equilibrium exchange rate) often changes considerably between different periods for a number of reasons. Firstly, it can be the result of changes in exogenous variables. For example, world commodity prices, which are very volatile, appear to play an important role. Secondly, it can be the result of outliers. If, for example, the output gap is at extreme values, our model might give particularly inaccurate estimates. Finally, our current account model may have a poor fit over the specific period chosen. This can also affect the estimated equilibrium value.
3.3 Estimated Relationship between the Exchange Rate and the Current Account
We now have an equation for the underlying current account, as outlined in Step 2 of the procedure described in Section 2.2. Step 3 involves solving the underlying current account equation KA = CA (E, Z) for the exchange rate, assuming different values of the target current account. This can be done algebraically once the exogenous variables Z have been set to their values in a specific reference period.
Table 2 summarises the results for the implied trade-weighted exchange rate index (TWI) equilibrium evaluated at some alternative reference points. Figure 6, which is the estimated equivalent to Figure 1 in Section 2.2, illustrates these results graphically. As predicted by theory, a larger current account deficit is consistent with an appreciation of the exchange rate. However, the estimated equilibrium exchange rate varies considerably over different reference periods, thus emphasising the uncertainty attached to any specific number.
| Ratio of current account to GDP Percentage points |
|||||
|---|---|---|---|---|---|
| Reference period | −6 | −5 | −4 | −3 | −2 |
| 1996:Q2 | 79.5 | 68.8 | 60.7 | 54.6 | 49.8 |
| 1998:Q2 | 53.8 | 47.8 | 43.2 | 39.5 | 36.4 |
| 2000:Q2 | 66.5 | 58.4 | 52.3 | 47.5 | 43.6 |
| 1992–2000 | 70.0 | 60.3 | 53.5 | 48.3 | 44.1 |
|
Notes: Due to data constraints for the NID component denominated in foreign currency, we can evaluate the equilibrium exchange rate only up to 2000. The measure of the output gaps used for the specific reference periods is described in Appendix A. In calculating the figures in the 1992–2000 row, we assume an average output gap of zero over this period for both Australia and the world. |
|||||
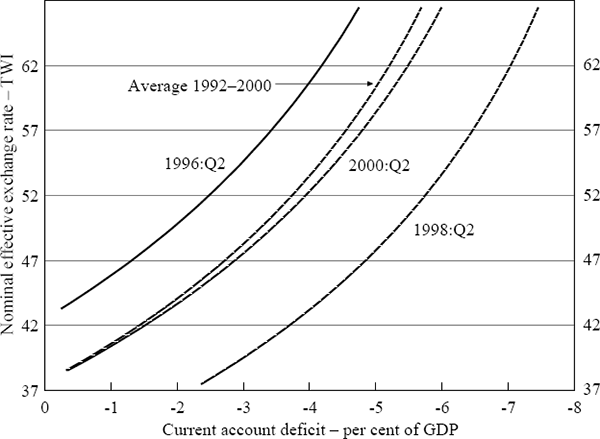
The variation of the underlying current account across different reference periods is due to changes in the exogenous variables which can affect the estimated exchange rate in two ways. First, the calculated equilibrium exchange rate is sensitive to the values of the exogenous variables in the reference period, especially if those values are outliers. Second, since those exogenous variables can change through time, the equilibrium exchange rate can also change through time.
We can calculate the elasticity in the implied equilibrium exchange rate with respect to changes in exogenous parameters by evaluating the total differential of Equation (3). We concentrate on changes in output, foreign prices P*,[11] net foreign income NID and in the capital account.
where caz is the partial derivative of ca with respect to z. Solving the differential for the exchange rate shows how it must move to keep both sides of the current account identity equal to each other in response to changes in P*, Y, Y*, NID or KA.
The elasticities caz can be derived analytically from the estimated parameters of the current account components. In principle, they can be evaluated using any reference period. To illustrate, we evaluated all the partial derivatives in the second quarter of 2000 and obtained the empirical equivalent to Equation (9). We expressed some variables in percentage changes (in lower case and denoted by hats), and solved for the exchange rate:
The first and second terms on the right-hand side reflect the adjustment necessary to attain internal balance. Closing a negative domestic output gap of 1 percentage point of GDP for a given current account level is consistent with an estimated medium-term depreciation of the exchange rate by around 4 per cent. Without this depreciation, the stronger demand would take the current account away from the target level, due to the increased imports. Closing a 1 per cent foreign output gap would be consistent with an appreciation of the exchange rate by 0.4 per cent, which is about 10 times less then the effect of closing the domestic output gap. The coefficient on world GDP seems low, but it will be recalled that we are price takers for resource and agricultural exports. In these cases, changes in world demand effect exports mainly via their effects on export prices.
The most important coefficient in this equation is the semi-elasticity with respect to the current account to GDP ratio. Our model implies that an increase in the target capital account deficit of 1 percentage point of GDP would be consistent with about a 10 per cent appreciation of the equilibrium exchange rate in the medium term. Our value of 10 per cent is rather large compared with existing studies for other countries such as WD, who find elasticities around 5–7 per cent. However, this elasticity is the inverse of the elasticity of the current account with respect to the exchange rate.[12] As noted by Goldstein and Khan (1985), estimated trade elasticities in the vicinity of zero are not uncommon. The viability of the macroeconomic balance approach depends upon this elasticity not being close to zero. In this case, implausibly large movements of the exchange rate may be needed to match the underlying current account with the assumed capital account value. As it is, this elasticity is 0.1, that is, a 1 per cent depreciation in the exchange rate raises the current account balance by 0.1 per cent of GDP.
Table 3 illustrates the results of Equation (10). It shows the estimated medium-term exchange rate elasticity with respect to changes in the output gap and the (target) capital account.
| Changes in KAtarget Per cent of GDP |
Closing domestic output gap Percentage points |
|||||||
|---|---|---|---|---|---|---|---|---|
| 1.5 | 1.0 | 0.5 | 0.0 | −0.5 | −1.0 | −1.5 | ||
| −2 | −15 | −17 | −19 | −21 | −23 | −25 | −27 | |
| −1 | −5 | −7 | −9 | −11 | −13 | −15 | −17 | |
| 0 | 6 | 4 | 2 | 0 | −2 | −4 | −6 | External balance |
| 1 | 17 | 15 | 13 | 11 | 9 | 7 | 5 | |
| 2 | 27 | 25 | 23 | 21 | 19 | 17 | 15 | |
| Internal balance |
||||||||
A current account deficit leads to continuing accumulation of foreign liabilities. The fourth term in Equation (10) demonstrates that the feedback effects of such accumulation onto the exchange rate are likely to be small. If net foreign liabilities grow at a faster rate than GDP, so that, for example, NID/GDP rises by 1 percentage point, the proportional change of the equilibrium exchange rate is −0.1.
The last term on the right-hand side is the independent effect of export prices on the equilibrium exchange rate. Since an increase in foreign export prices will boost export revenues, the exchange rate must appreciate in order to maintain the same current account. The coefficient on export prices seems high, compared with other studies that find a terms-of-trade elasticity of between 0.4 and 1.0 (Gruen and Wilkinson 1991; Blundell-Wignall et al 1993; Tarditi 1996). However, it is to be expected that changes to export prices may be associated with increases in domestic GDP. For example, a 10 per cent improvement of the terms of trade could be expected to increase domestic GDP by around 2 per cent.[13] Based on Equation (10), this leads to an appreciation of approximately 10 per cent (= 1.9·10 − 4.1·2). Thus the full elasticity is approximately unity, sitting at one end of the range of the earlier studies.
3.4 Sensitivity Analysis
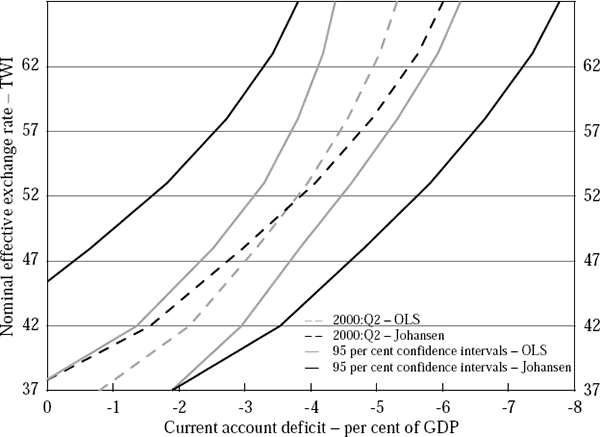
In Section 3.3 we have stressed the role of the exogenous variables as a source of uncertainty of our empirical results. However, like any estimated equation, our results are also subject to uncertainty arising from the use of econometric estimation techniques. Therefore, this section reports the results of a Monte-Carlo simulation of the confidence intervals around our estimates in Figure 6, evaluated in the second quarter of 2000. The confidence intervals are only indicative, since it is necessary to make a number of assumptions about the joint distributions of the estimated coefficients.
Our variable of interest – the estimated current account – is the sum of log-normally distributed variables (the trade equations are estimated in log-linear form) and normally distributed variables (NID and net transfer). Since we do not know the theoretical distribution of this sum, we use Monte-Carlo simulations to derive the confidence interval around the estimate of the current account.
The simulation consists of 5,000 random draws of the estimated coefficients, using the joint distributions from each estimated equation. We assume that the covariances between the components that we have estimated separately are zero.
These random draws, combined with realisations of the variables for 2000:Q2, give 5,000 estimates of the underlying current account which we use to derive 95 per cent confidence intervals around the central estimate.
We have evaluated two benchmark cases. The first case uses the Johansen estimates from the results presented in Section 3.3. As the joint distribution of the constant with the other cointegrating parameter is not known, we had to calculate a value for the constant for each iteration.[14] The second case uses OLS estimates for all equations.[15] These have the advantage that the joint distribution of all coefficients of an individual equation is known.
Figure 7 shows the central estimates and the 95 per cent confidence intervals (solid lines) for both cases. The grey lines show the OLS estimates. As these estimates are numerically different from the Johansen estimates, the resulting exchange rate equation has a slightly different slope. The black lines show the estimates based on Johansen, with the central line equivalent to 2000:Q2 in Figure 6. The confidence intervals are wider than the OLS estimates, as the Johansen procedure involves the estimation of more parameters. In the case of the Johansen estimates, the confidence intervals encompass a range as wide as 20 index points on the TWI exchange rate.
Footnotes
In the first instance we relied on the Johansen procedure to test the cointegration relationship. We also compared the results to ECM and OLS estimates. Appendix C contains the details. [5]
WD solve for a real exchange rate, but one has then to estimate (or impose) a relationship between the different real exchange rates used for the estimation of the trade equations. [6]
We are grateful to Tony Webber for helping us clarify these simultaneity issues. [7]
The service import equations do not work very well; see Appendix B. [8]
This is not as unrealistic as it sounds. The effect of world output on export volumes comes through commodity prices. [9]
The underlying current account is the sum of log-normally distributed variables, as the trade equations are estimated in log-linear form. We corrected for the transformation bias (of the mean) in the logarithmic regression using estimates of the covariance matrices as described in Section 3.4. In our case, the mean bias is very small – at around 1 per cent for the evaluation periods chosen. [10]
Since we have a number of different foreign prices, we set their rates of change equal for the purpose of this exercise. [11]
This elasticity is sometimes related to the so-called Marshall-Lerner conditions for a depreciation to impact positively upon the current account. However, the Marshall-Lerner conditions have limited relevance for Australia. First, they are neither sufficient nor necessary if the current account starts from a position of deficit. Second, and more importantly, the conditions are only relevant where a country is a price setter for all of its exports. [12]
Using the terms-of-trade adjusted GDP (Edey, Kerrison and Menzies 1987) ytot = y + tot x − x. Since exports are roughly 20 per cent of GDP, a 10 per cent improvement in export prices is equivalent to a 2 per cent increase in ytot. [13]
The theoretical joint distribution of the long-run coefficients was taken from Johansen (1991). In the Johansen procedure, the constant in
the cointegration space is calculated from 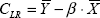 (where
Y and X denote the cointegration variables and β is the
vector of coefficients). As there is no theoretical expression for the covariance with
the other cointegrating parameters, we did not draw a series for CLR
randomly. Instead, we calculated it using this formula for each draw of the other
cointegration coefficients. In our case, the constant has a very large (sample)
covariance with the cointegration coefficients on output, which impacts substantially on
the width of our confidence intervals.
[14]
(where
Y and X denote the cointegration variables and β is the
vector of coefficients). As there is no theoretical expression for the covariance with
the other cointegrating parameters, we did not draw a series for CLR
randomly. Instead, we calculated it using this formula for each draw of the other
cointegration coefficients. In our case, the constant has a very large (sample)
covariance with the cointegration coefficients on output, which impacts substantially on
the width of our confidence intervals.
[14]
When estimating cointegrating vectors in I(1) systems, OLS is a super-consistent estimator but contains second-order biases. The Johansen estimator should in principle be preferred since it removes the bias in the median and the simultaneous equation bias (Banerjee et al 1993). This said, given our sample size, possible small sample problems of either estimator might be of more concern. [15]