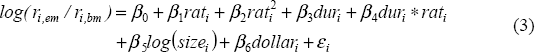RDP 2003-02: Do Collective Action Clauses Influence Bond Yields? New Evidence from Emerging Markets 4. Were Collective Action Clauses Priced in Early 2003?
March 2003
- Download the Paper 92KB
4.1 Methodology
In this section, we largely follow the methodology of Becker, Richards and Thaicharoen (forthcoming) in examining the impact of the presence or absence of CACs in the pricing of a large sample of bonds trading on the secondary market. Whereas those authors concentrated on market pricing as of 30 June 1998 and 30 June 2000, we focus on a more recent date, namely 31 January 2003.
Our dependent variable is the log of the ratio of the yield on the emerging market bond i to the yield on the corresponding mature market benchmark bond, and is denoted by log(ri,em/ri,bm).[14] We initially include the full sample of bonds from all emerging market countries. We regress the yield variable against a number of variables for the characteristics of the bond. These include: the average credit rating for the bond from Moody's and Standard and Poor's (rati);[15] the modified duration of the bond (duri); the US dollar equivalent of the amount of each bond on issue (sizei); and a dummy for US dollar-denominated (rather than European currency denominated) bonds (dollari).
Since theory offers little guidance as to the exact functional form of the relationship between the explanatory variables, we tested different functional forms in search of a parsimonious equation that explained the data reasonably well. The basic equation is as follows:
The squared rating term is included to allow for a non-linear relationship for lower-rated bonds, and the term interacting the duration and ratings variable is included to allow for the observation that, for poorly rated borrowers, yields often fall rather than rise with duration.
We then included a dummy variable (CACi) taking the value of unity if the bond includes CACs (based on English governing law). In addition, since some have argued that the impact of CACs on yields should be somewhat dependent upon the credit quality of the issuer, we also included an interaction term with the credit rating variable.
Although most major emerging market issuers have issued bonds with and without CACs, many of the bonds in our sample of secondary market yields are from countries that have issued bonds with only one type of contractual form. If the decision by countries to choose a particular contractual form were related to their creditworthiness (or to some other determinant of spreads), then it would be possible that estimates of the impact of governing law might be biased due to endogeneity. In practice we believe this is not a major issue, based both on market practice,[16] and because we expect that our credit rating variable is a fairly comprehensive measure of the information about creditworthiness that is available at any time.
Nonetheless, to address the possible problem of endogeneity we also estimate an equation for yields including only those countries that have bonds outstanding with and without CACs. As discussed by Becker, Richards and Thaicharoen (forthcoming) this is equivalent to a fixed effects correction for endogeneity and enables us to avoid the problems of endogeneity corrections based on instrumental variables. In estimating this model, we include a dummy variable for each country, but no longer need to include the credit ratings variables.
4.2 Data
We obtained data for secondary market yields for a large sample of sovereign bonds (excluding Brady bonds) from the Merrill Lynch Global Index database. We also obtained data for the currency and modified duration of each bond from Merrill Lynch. We focus on data for 31 January 2003. The sample includes sovereign borrowers rated by Standard and Poor's, and Moody's between A+/A1 and B−/B3. We omit issuance in Japanese yen, and limit our sample to issuance in US dollars and major European currencies.
We obtained data on the governing law of all bonds in our sample from Bondware or Bloomberg. Data on long-term foreign currency debt ratings were obtained from Bloomberg and transformed into a numerical variable (as described in Footnote 15). In the event of a split rating between Moody's and Standard and Poor's we use the average numerical rating.
Our final sample includes 216 bonds from 39 countries.[17] The sample of countries with bonds both with and without CACs includes 119 bonds from 13 countries, including Brazil, Croatia, Hungary, Israel, Lebanon, Malaysia, the Philippines, Poland, Russia, Slovenia, South Africa, Tunisia and Turkey. The latter group includes 48 bonds with CACs and 71 bonds without CACs.
4.3 Results
The initial specification tests to determine the functional form shown in Equation (3) were conducted before the inclusion of the CACs variable(s). In addition to the variables shown in Equation (3), we include separate country dummies for three countries (Brazil, Mexico and Turkey) that each represent more than 10 per cent of the total number of bonds in our sample (though the results that follow are not dependent on this). The parameter estimates for the basic model are shown in the first column of results of Table 3.[18] The results show that yields are higher for bonds with poor credit ratings and longer durations, and for dollar-denominated issues (relative to issuance in European currencies). The signs of each of these estimated impacts accords with conventional wisdom on market pricing, and the interaction terms also take the expected signs. The estimate on the variable for the size of the issue is negative, which may reflect a liquidity effect, with larger bonds with greater liquidity having lower yields.
| Sample – all 216 bonds from 39
issuers |
Sample – 119 bonds from 13 issuers with bonds both with and without CACs | |||||
|---|---|---|---|---|---|---|
| Explanatory variable |
No CAC variable |
CAC dummy variable included | CAC dummy and interaction term included | CAC dummy variable included | CAC dummy and interaction term included | |
| Constant | −0.293(1.4) | −0.283(1.4) | −0.314(1.5) | na | na | |
| Rating | 0.100(2.9) | 0.098(2.9) | 0.103(3.0) | na | na | |
| Rating-squared | 0.002(1.5) | 0.002(1.6) | 0.002(1.5) | na | na | |
| Duration | 0.066(4.7) | 0.068(4.7) | 0.068(4.6) | 0.054(3.4) | 0.055(3.3) | |
| Duration* rating | −0.009(6.2) | −0.009(6.2) | −0.009(6.2) | −0.009(5.5) | −0.009(5.4) | |
| Dollar-denominated | 0.152(4.7) | 0.109(3.0) | 0.111(3.0) | 0.123(4.4) | 0.117(4.0) | |
| Log (amount) | −0.053(3.6) | −0.043(2.6) | −0.043(2.6) | −0.031(1.2) | −0.025(0.9) | |
| CACs | na | −0.087(2.8) | −0.049(0.6) | 0.022(0.9) | −0.057(0.8) | |
| CACs* rating | na | na | −0.003(0.5) | na | 0.007(1.1) | |
| Adjusted R2 | 0.891 | 0.896 | 0.895 | 0.959 | 0.958 | |
|
Notes: This table shows estimates of Equation (3) to estimate the effect of the inclusion of CACs on yields on emerging market bonds. The dependent variable is given by log(ri,em/ri,bm), i.e., the log of the ratio of the yield on the emerging market bond relative to the yield on the corresponding mature market benchmark bond. T-statistics are shown in parentheses and are based on heteroskedasticity-consistent standard errors. |
||||||
We test for the importance of CACs in determining yields by first including a simple zero/one dummy variable that takes the value of one for English law bonds. The results in the second column suggest that the use of CACs was associated lower yields for the full sample of bonds. Although the parameter estimate is statistically significant, we hesitate to rely too much on any particular estimate, given that the previous work of Becker, Richards and Thaicharoen (forthcoming) shows that such coefficient estimates tend to jump around somewhat, while never deviating much from zero.
We then test whether the impact of CACs might be somewhat dependent upon credit quality by including a term that interacts the CAC dummy with the numerical ratings variable. The results in the third column indicate that the interaction term is completely insignificant, and that the basic CACs variable is no longer significant, although the parameter estimate remains negative.
When we limit our sample to 13 countries to conduct a test equivalent to the fixed-effects endogeneity correction, we exclude the rating and rating-squared variables, and instead include separate country dummies for each country. The results are shown in the fourth column, and for brevity exclude the parameter estimates for the country dummies. The results indicate that the CACs variable is now modestly positive, though it remains statistically insignificant. Our final set of results in the fifth column also includes a variable interacting the CACs variable with the numerical ratings variable. The point estimates suggest that CACs are associated with lower yields for high-rated issuers, but higher yields for low-rated issuers. However, these impacts are not statistically significant since both CACs variables are insignificant.
We summarise the results from Table 3 (and other related results which are not shown) as follows. While some of the results suggest that CACs are associated with higher yields, others suggest they are associated with lower yields, and most of the estimates are insignificant: the only significant result was in the second column and was that CACs were associated with lower yields. This pattern of variable, but almost always insignificant, estimates is exactly what one would expect if CACs have no impact on yields. These results from a large sample of bonds in early 2003 are similar to the results obtained for earlier samples in Becker, Richards and Thaicharoen (forthcoming) and suggest that the presence or absence of CACs is not a factor that is priced in the secondary market trading of emerging market bonds.
Footnotes
The reason we use this transformation rather than the log of the spread is that the latter approaches negative infinity as the spread approaches zero, implying that bonds with very low spreads may have an undue impact on the estimates. [14]
The credit rating variable is expressed in terms of the standard numerical rating, with AAA/Aaa set to 1 and B−/B3 set to 16. [15]
Becker, Richards and Thaicharoen (forthcoming) provide analysis showing that the use of governing law is highly correlated with factors such as the currency and market of issue, and the nationality of the investment bank that is the lead manager of the issue. Dammers (2002) also notes that the choice of governing law and use of CACs is not a primary decision for issuers or investors, but is likely to reflect the type of documentation typically used by the lead manager's lawyers. [16]
The countries include Bahrain, Barbados, Brazil, Chile, China, Colombia, Costa Rica, Croatia, Cyprus, Dominican Republic, Egypt, El Salvador, Estonia, Guatemala, Hungary, Israel, Jamaica, Kazakhstan, Korea, Latvia, Lebanon, Lithuania, Malaysia, Mexico, Panama, Peru, Philippines, Poland, Qatar, Romania, Russia, Slovenia, Slovak Republic, South Africa, Thailand, Tunisia, Turkey, Ukraine and Uruguay. Based on the information in Footnote 9, we define six issues by Egypt, Lebanon and Qatar as including CACs, even though they occurred under New York governing law. [17]
For brevity, we do not show the separate country dummies for Brazil, Mexico and Turkey for the first three specifications, nor the 13 country dummies in the last two specifications. [18]