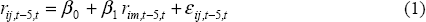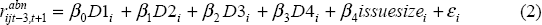RDP 2003-02: Do Collective Action Clauses Influence Bond Yields? New Evidence from Emerging Markets 3. Did Decisions on Collective Action Clauses on New Issues Affect Secondary Market Spreads?
March 2003
- Download the Paper 92KB
3.1 Introduction
The argument that the use or non-use of CACs should influence yields and borrowing costs is usually made along the following lines. Opponents of CACs have generally argued that the likelihood that borrowers will choose to honour their obligations may be altered by the use or non-use of CACs, and that the inclusion of CACs will signal a reduced likelihood of full repayment to bondholders. In essence the argument is that if restructuring is made easier then borrowers are more likely to seek to restructure and reduce their obligations, even if they are perfectly able to honour them. By contrast, proponents of CACs have typically argued that history shows that sovereign borrowers do not willingly seek to renege on their contracts so that the use or non-use of CACs contains no signal about creditworthiness. However, in the event of the financial distress of the borrower the inclusion of CACs will increase the probability of a smooth restructuring rather than a messy default, and will therefore result in reduced losses to bondholders.
The tests in this section make no assumptions about which of these effects is the dominant one, and whether proponents or opponents of CACs are ‘correct’. Instead, we initially simply seek to test if we can find any evidence that the use of CACs has affected yields at all, without any priors about which direction this effect should take.
Our test is based on the notion that if the decision to use or not use CACs contains information that is important to investors, then it influences not only the value of a bond at the time of issue but also affects the value of the outstanding stock of previously issued bonds. For example, if a borrower has previously issued bonds without (with) CACs, then the decision to issue bonds with (without) CACs may – if there is any merit to the argument of the opponents of CACs – signal a decline (improvement) in the creditworthiness of the borrower. This should be reflected not only in higher (lower) borrowing costs for the bond that contains the change in contractual terms, but also higher (lower) yields on the outstanding stock of bonds, because the latest issuance decision conveys information to the market that is relevant for the valuation of those bonds.
Alternatively, even if there is no signal about the borrower's willingness to repay, the arguments of the proponents of CACs might suggest there could still be an impact on yields, albeit in the opposite direction to the effect posited in the previous paragraph. For example, a shift towards CACs may convey information about the likelihood of a smooth (and value-preserving) restructuring rather than a messy (and value-destroying) default. For example, if the probability of a smooth restructuring is a function of the proportion of bonds with or without CACs, then decisions to change the type of issuance convey information about the likely ease of restructuring and could therefore result in changes in yields and prices in the secondary market.
3.2 Methodology
The preceding discussion can be re-expressed as a testable hypothesis: if the use or non-use of CACs is value-relevant for investors, changes in the nature of the majority action clause relative to previous issuance will impact on the value of the issuer's outstanding stock of debt.
We test this hypothesis via an event study of abnormal returns in the secondary market pricing of the existing stock of debt. We divide all debt issues (or events, denoted by i) in our sample based on whether the issue included CACs or not, and whether it represented a change in the use of CACs from the previous issue. This enables us to create four mutually exclusive dummy variables: D1i, where the issuer did not use CACs in either the current issue or the previous issue; D2i, where the issuer used CACs in both the current issue and the previous issue; D3i, where the issuer used CACs in the current issue but not in the previous issue; and D4i, where the issuer did not use CACs in the current issue, but did so in the previous issue.
One key methodological question in conducting the test is the definition of the abnormal return and the ‘event window’. For every event we know the day when the bond issue was announced to the market as occurring on that day. If this was indeed the day that the market learned everything about the issue, then we could conduct an event study for abnormal returns on that day. However, for most bond issues, the marketing of an issue typically occurs for some period before the announcement to the market that the issue is taking place on the day in question. Any assumption of the standard period of ‘pre-marketing’ will be somewhat arbitrary, but for the purposes of this study we choose to focus on a five day event window, starting three trading days before the announcement, and ending one day afterwards. Thus treating the day of the announcement of the issue as t = 0, our event window is defined as the period from t = −3 to t = +1. We would not argue that all investors become aware of the nature of the contractual terms of the issue in this window, merely that a sufficiently large fraction of investors learn about the terms of the bond in this window to have an effect on secondary market pricing if the news about the contractual terms is indeed value-relevant.
Given the definition of the event window, we define the ‘estimation window’ as the 100 day interval from t = −103 to t = −4. We then estimate a market model for this window for each event i and borrower j, by regressing the daily return on the relevant emerging market issuer (rijt) on the return on a broad portfolio of emerging market bonds (rimt). To take account of possible illiquidity in secondary market bond pricing, we estimate our market model using overlapping five-day returns. The equation we estimate is therefore given by:
Using the parameter estimates from Equation (1) we calculate a predicted return for the five-day event window, and then define the abnormal return (rabn) as the actual return less the predicted return. We then regress this abnormal return on the four dummy variables for the nature of the contractual terms, and the size of the bond issue as a ratio to national GDP, denoted issuesizet:[11]
In addition to estimating Equation (2) using abnormal returns, we also estimate it in standardised terms, i.e., by dividing the event-window abnormal returns by the standard error of the predicted return (based on Newey-West standard errors to account for the moving average error term that is introduced through the use of overlapping returns). The distribution of these standardised abnormal returns will have a unit variance if event-window returns are drawn from the same distribution as estimation-window returns.
3.3 Data
Data for this part of the study are based on bond issuance data in the Bondware database and secondary market bond index data from JPMorgan Chase.
From Bondware, we obtained data for all issuance (excluding Brady bonds) by sovereigns rated A+/A1 or lower by Standard and Poor's, and Moody's. We then focused on issuance in US$ or major European currencies into the Euromarket, US market or global market. We then limited the sample to all issuance that occurred under New York, German, English or Luxembourg governing laws. Since CACs are not customary in bonds issued under the first two governing laws, those bonds represent the issuance that occurred without CACs, while bonds issued under the latter two governing laws represent our sample of bonds issued with CACs.
The resulting sample of bonds from Bondware represents a sample where we can reasonably say that even after deciding on the currency of issue, borrowers had a choice in whether or not to use CACs. We then focus on countries that switched between using or not using CACs on at least two occasions in the sample.
We obtained data for total return indices for the existing secondary market stock of bonds from JPMorgan Chase. We use the EMBI Global indices which are available on a daily basis from the start of 1994. These indices measure the daily change in the valuation of the stock of securities issued by each country that meet certain requirements in terms of size and liquidity of each issue. In each case we required the existence of a sufficiently long time-series of returns to enable the estimation of a market model prior to the event window. We use the US dollar indices in all cases, even in cases where the bond issue was denominated in a European currency. The implicit assumption is that the two markets are not totally segmented and that news that is revealed in one market will also be reflected in pricing in the other market.
The intersection of the Bondware and JPMorgan Chase data leaves us with data from 10 countries which have switched at least twice between using and not using CACs, and for which we have the required secondary market returns data. One potential problem with the data is that they are heavily weighted toward Argentina, given that country's heavy issuance over 1991–2001. To reduce the weight of Argentina, we limit our universe of Argentinean issues to those greater than US$400 million in size.
The resulting sample includes 204 bond issues from the 10 countries, including Argentina, Brazil, Croatia, Malaysia, the Philippines, Poland, Russia, South Africa, Turkey and Venezuela. The sample includes 87 events where the borrower switched in its usage of CACs (43 to using CACs, and 44 from using CACs), and 117 events where there was no change in contractual form (26 using CACs and 91 not using CACs).
3.4 Results
The data for abnormal returns for the 204 events described above have a mean that is slightly negative, at around −0.15 per cent. This might be viewed as evidence that new issuance is typically associated with a very slight fall in the value of the existing stock of debt, because it represents an addition to the outstanding stock of debt. However, when we add a variable for the size of the new issuance as an explanator of the abnormal return, the parameter estimate is far from statistically significant (although it is negative) so we cannot attribute much of the average negative abnormal return to a ‘supply-shock’ explanation.[12]
The results from estimating Equation (2) are provided in Table 2. If the use of CACs was viewed negatively by the markets, changes from using CACs to not using CACs should be associated with positive abnormal returns whereas changes to using CACs should be associated with negative abnormal returns. Furthermore, decisions to continue the use of CACs should be associated with more negative returns than decisions to continue not using CACs. However, the first column of results provides no support for these propositions with none of the parameter estimates being statistically significant.
| Dependent variable | ||
|---|---|---|
| Explanatory variable | Abnormal return | Standardised abnormal return |
| D1 | ||
| CACs not included, no change in contractual form | −0.22(1.8) | −0.23(1.7) |
| D2 | ||
| CACs included, no change in contractual form | −0.05(0.3) | −0.26(1.3) |
| D3 | ||
| Change in contractual form to CACs | −0.07(0.5) | −0.06(0.4) |
| D4 | ||
| Change in contractual form to excluding CACs | 0.08(0.5) | −0.08(0.5) |
| Issue size/GDP | −0.14(0.9) | −0.14(0.7) |
| Adjusted R2 | 0.0012 | −0.0073 |
|
Notes: This table shows the results from an event study to investigate if decisions on whether or not CACs are included in new bond issues affect the pricing of a country's existing debt in the secondary market. The results show estimates of Equation (2) with the dependent variable first defined as the abnormal return (in per cent) around the event date and then as the standardised abnormal return around the event date. The variables D1–D4 are mutually exclusive variables defined by whether or not CACs are included in a new issue, and whether this was a change from the previous issue. T-statistics are shown in parentheses based on heteroskedasticity-consistent standard errors. |
||
Similarly, the results for standardised abnormal returns also fail to show any evidence consistent with the view that the use of CACs is penalised by the financial markets. Indeed, what is striking about these results is that the adjusted R2 for both regressions are approximately zero, suggesting the abnormal returns on the existing stock of debt are essentially independent of decisions about the governing law of bonds (and the size of the new issue).[13]
These results are complementary to, but consistent with, the results of Becker, Richards and Thaicharoen (forthcoming) and Tsatsaronis (1999). Whereas those authors show that an issuer's decisions about the use or non-use of CACs have historically had no impact on the pricing of its new debt issues, the current results show that these decisions have also had no impact on the pricing of issuer's existing stock of debt. These results would appear consistent with the reality that issuers have frequently switched between using CACs and not using CACs, and investors have been apparently unconcerned by decisions on the exact form of the contractual terms of bonds.
Footnotes
Since the four dummy variables are mutually exclusive, we do not include a constant term. [11]
It may not be surprising that the change in secondary market prices is largely independent of the size of the new issue if issuers typically have sufficient flexibility in new issuance to adjust its timing and magnitude to minimise the impact on the existing yield curve (i.e., by not proceeding with a planned issue if it is likely to result in a substantial increase in yields, and in increasing the size of an issue if there is strong demand for it). [12]
As a robustness check, we have also examined the impact of including credit ratings interaction terms with the dummy variables, and still find no evidence that choices on contractual terms affect abnormal returns. In addition, since 131 of the 204 events in the sample relate to just three issuers (Argentina, Brazil and Turkey) we have also estimated the equations excluding these three large issuers. The results are little changed. [13]