RDP 2000-07: The Effect of Uncertainty on Monetary Policy: How Good are the Brakes? 5. Results
October 2000
- Download the Paper 278KB
The benchmark for interest rate variability we use is that which results from the inclusion only of additive uncertainty in the model. As can be seen in Table 3, under additive uncertainty, the path of policy interest rates generated by the model is extremely volatile compared to that observed in practice. The average change in policy interest rates is also considerably greater than that observed in practice. The average change in policy interest rates generated by the model was 8 percentage points each quarter, and the standard deviation of these changes was around 5.6 percentage points.[14] Figure 4 shows the distribution of the average absolute interest rate change that resulted from each of the 50 draws, and illustrates the positive skew in the distribution.
| Observed variability |
Model with additive uncertainty only |
|||||
|---|---|---|---|---|---|---|
| 1985–1999 | 1993–1999 | |||||
| Real | Nominal | Real | Nominal | |||
| Absolute change in policy interest rates |Δr| |
– Mean | 0.9 | 0.9 | 0.3 | 0.3 | 8.0 |
| – Median | 0.6 | 0.7 | 0.2 | 0.1 | 6.8 | |
| Std dev |Δr| | – Mean | 0.9 | 0.9 | 0.3 | 0.3 | 5.8 |
| – Median | na | na | na | na | 5.6 | |
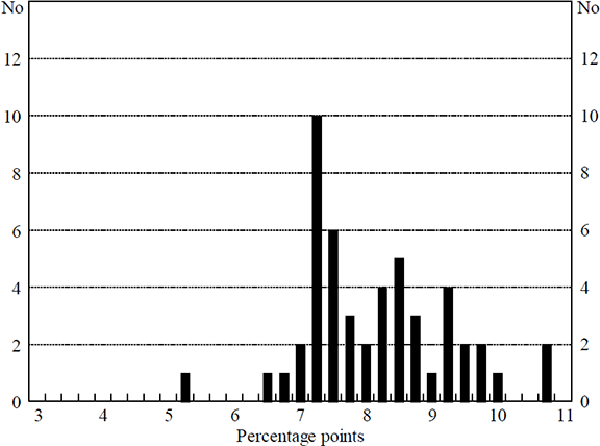
Here, as in all the other simulations that are discussed in this section, the paths of policy interest rates that were generated by the model exhibit minimal (if any) autocorrelation in interest rate changes, in contrast to that observed in practice. That is, none of the forms of uncertainty examined in this paper are able to explain the relative frequency of continuations and reversals in policy changes.
5.1 Parameter uncertainty
Table 4 summarises the results when uncertainty about the parameters is incorporated in the model. At this stage, there is no mean uncertainty: the policy-maker assumes that the mean of each parameter is as estimated in the model. We did not allow for uncertainty about every parameter in the model, but rather focused on the 10 most important parameters of the model in the output, inflation, unit labour cost, import price and real exchange rate equations.
| Form of uncertainty | Additive only | Full parameter | Interest rate sensitivity of output | Phillips curve term in wage equation | Relative importance of domestic and imported inflation | Adjustment of output to potential in output equation | |
|---|---|---|---|---|---|---|---|
| |Δr| | – Mean | 8.0 | 8.4 | 7.7 | 8.0 | 8.0 | 8.1 |
| – Median | 6.8 | 7.1 | 6.5 | 6.8 | 6.8 | 6.8 | |
| Std dev |Δr| | – Mean | 5.8 | 6.1 | 5.6 | 5.8 | 5.8 | 5.8 |
| – Median | 5.6 | 6.1 | 5.5 | 5.6 | 5.6 | 5.7 | |
The table shows that the introduction of ‘full’ parameter uncertainty does not greatly affect the variability in policy interest rates compared with that when only additive uncertainty is considered, and in fact, marginally increases it. Uncertainty about the sensitivity of output to interest rate changes seems to decrease interest rate variability only slightly.
These results are in contrast to those in Sack (2000) and Martin and Salmon (1999), where parameter uncertainty increased the smoothness of policy substantially. One possible explanation for the different findings is that, as Shuetrim and Thompson (1999) show empirically and Söderström (1999) demonstrates analytically, whether parameter uncertainty increases smoothness depends on the nature of the uncertainty and its interaction with the lag structure of the economy. Secondly, Sack and Martin and Salmon use the single observed path of shocks which affected the US and UK economies (that they obtain from their models) to derive their results, whereas here we used multiple paths.
Consequently, we conducted a similar exercise to Sack and Martin and Salmon by simulating the model with the observed residuals over the sample period, and then introducing the various forms of uncertainty. Table 5 summarises the results from this exercise.
| Form of uncertainty | Additive only | Full parameter | Interest rate sensitivity | |
|---|---|---|---|---|
| |Δr| | – Mean | 4.3 | 4.8 | 4.3 |
| – Median | 3.9 | 4.0 | 4.1 | |
| Std dev |Δr| | – Mean | 2.8 | 3.0 | 2.9 |
| – Median | 2.8 | 3.0 | 2.9 | |
These results show that interest rate variability is considerably reduced when only the path of historical shocks is considered. The second column of the table shows that, in this instance, full parameter uncertainty increases interest rate variability, but if there is only uncertainty about the sensitivity of output to the interest rate, then interest rate variability is approximately unchanged.
The interest rate variability is lower with the historical shocks than most of the draws shown in Figure 4 because the path of the shocks matters. The historical shocks are not completely random, unlike those that underpin Figure 4. The draws in our simulations are taken from a normal distribution with no serial correlation. While the historical shocks have no significant serial correlation and are not significantly different from a normal distribution (in most cases), they have sufficient non-normality and serial correlation to generate the results in Table 5.
To further narrow down the interaction of the additive and parameter uncertainty, we ran a set of simulations where there was uncertainty only about the interest sensitivity parameter and the shock in the output equation (the results are not shown here). In this instance, interest rate variability was reduced when there was uncertainty about the interest rate parameter, a result similar to that found by Rudebusch (1999). This again highlights that the exact nature of the uncertainty affects the conclusions that can be drawn about the implications of uncertainty for interest rate variability.
5.2 Mean parameter uncertainty
The above results assume that the policy-maker believes that the mean effect of interest rate changes on output (say) is the same as that implied by the model estimated with the historical data. Next we allow the parameters in the economy to have different means from those in the estimated model and also allow the policy-maker to realise this fact, while still maintaining the same degree of uncertainty (that is, the variance of the parameter is not affected by a shift in its mean). Later, we will assume that the model's parameters are as estimated but the policy-maker believes them to be different.
We focus particularly on the effect of interest rate changes on output. Firstly, we increase the impact of interest rate changes on output by one standard deviation. That is, interest rate changes are now more powerful, and the policy-maker is aware of that fact. Figure 5 shows the impulse response of output to a one percentage point reduction in policy rates for one period under the estimated and the new parameter value, −0.15 and −0.19 respectively.
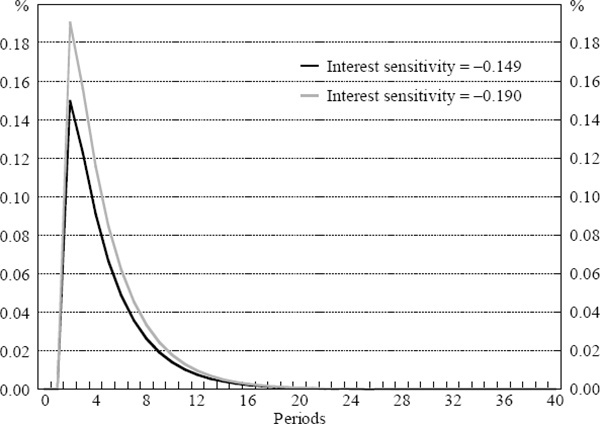
As noted in Section 3, whether increases in mean interest rate sensitivity increase policy smoothness depends on the coefficient of variation. Here, as the interest rate term is significant, one would expect that an increase in interest rate sensitivity would increase smoothness. The third and fourth columns of Table 6 show that this is certainly the case.
| Form of uncertainty | Additive only | Interest rate sensitivity parameter | Mean interest rate sensitivity – one std dev larger | Mean interest rate sensitivity – two std dev larger | Mean interest rate sensitivity – two std dev smaller | |
|---|---|---|---|---|---|---|
| |Δr| | – Mean | 8.0 | 7.6 | 6.0 | 5.0 | 14.4 |
| – Median | 6.8 | 6.5 | 5.1 | 4.2 | 12.2 | |
| Std dev |Δr| | – Mean | 5.8 | 5.6 | 4.6 | 3.6 | 10.4 |
| – Median | 5.6 | 5.5 | 4.3 | 3.6 | 10.4 | |
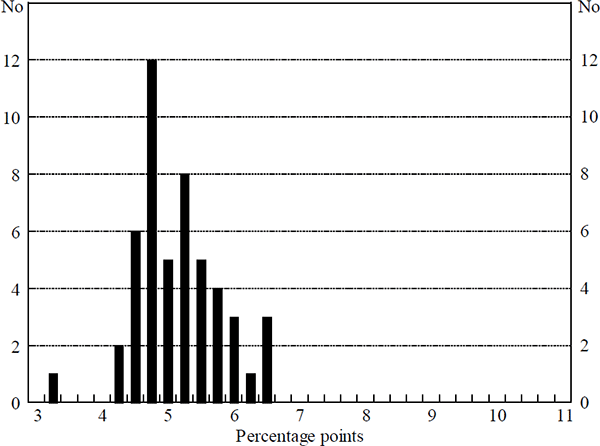
Interest rate variability is reduced by around 25 per cent with a one standard deviation increase in interest sensitivity. Figure 6 shows the frequency distribution of the average absolute change in policy interest rates in each path, that underpins the results in the third column. It shows the lower interest rate variability in each of the paths, compared to that illustrated in Figure 4.
The fourth column of the table shows that a two standard deviation increase in interest sensitivity decreases interest rate variability even further. If on the other hand, interest rate sensitivity is reduced by two standard deviations, the results in the fifth column illustrate that interest rate variability is substantially increased. This is because, in this instance, the economy is extremely insensitive to interest rate changes (the coefficient is close to zero).
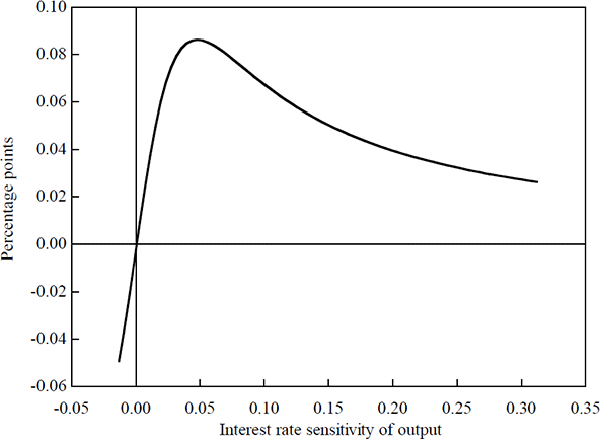
These results support the analysis in Section 3.3 above. As further evidence of this, Figure 7 traces out the optimal contemporaneous interest rate response to a temporary one per cent increase in output as the interest rate parameter is varied, that is, as the interest rate sensitivity of the economy is changed. The figure traces out a curve similar to that obtained analytically above in Figure 2.[15]
One caveat to these results is that we have confined the mean parameter uncertainty to the interest rate sensitivity of output. A shift in the mean of this parameter may be associated with changes in other equations in the model, thereby offsetting the impact on interest rate variability. However, re-estimating the output equation while imposing the higher interest rate coefficient did not affect the other coefficients significantly, but rather only resulted in larger residuals.
The above exercise assumes that the economy is more interest sensitive than that estimated, and that the policy-maker knows this. If instead, we assume that the model of the economy is, indeed, as estimated, but that the policy-maker believes the economy is more interest sensitive, we find that interest rate variability is again reduced, although not quite as much as in Table 6.[16]
In this situation, the variability of the economy as perceived by the policy-maker is increased in the same way that Brainard originally posited, thereby increasing smoothness in line with Brainard's original conclusion. Indeed, these results suggest that the policy-maker's beliefs about the effect of his or her actions on the economy have an important influence on the variability of policy interest rates.
Footnotes
Arguably, other parameters in the model might change quite significantly if such a volatile pattern of interest rate changes was the norm. [14]
If we assume that the policy-maker rules out outcomes where interest rates have a ‘perverse’ effect on activity, then the interest rate response continues to increase, as the interest sensitivity of the economy falls to zero. [15]
In each period, the policy-maker is surprised to find that the economy does not respond as much as expected to the change in interest rates. [16]