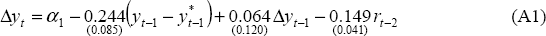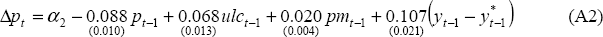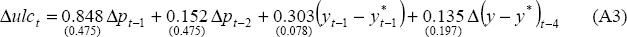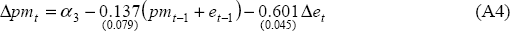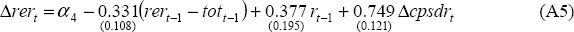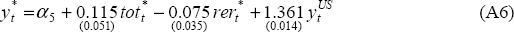RDP 2000-07: The Effect of Uncertainty on Monetary Policy: How Good are the Brakes? Appendix A: A Small Macroeconomic Model of Australia
October 2000
- Download the Paper 278KB
The model used in this paper is a simplified version of the model described in Beechey et al (2000). The motivation for each equation is provided there, along with additional references. The specification of each equation of the model along with the diagnostics are given below. All variables except for the interest rate are expressed in log levels; interest rates are expressed in annualised terms. Each equation is estimated from 1985:Q1 to 1998:Q4. In our simulations, the constants in each equation were calibrated so that the model possessed certain steady-state properties. All numbers expressed in parentheses are standard errors. Lags of variables were included, even when not significant, to allow for some dynamics in the model.
Endogenous variables
Output
 = 0.255 = 0.255
|
Standard Error = 0.007 |
| Jarque-Bera test: 1.97 [p=0.37] | LM(4) Test: 1.09 [p=0.37] |
| Durbin-Watson = 2.09 |
where y is real non-farm output, y* is potential output, and r is the real cash rate and rt = it − Δ4 pt where Δ4 pt = pt − pt−4 and i is the instrument of monetary policy.
Prices
 = 0.864 = 0.864
|
Standard Error = 0.002 |
| Jarque-Bera test: 1.12 [p=0.57] | LM(4) Test: 0.93 [p=0.45] |
| Durbin-Watson = 1.68 |
where p is the level of the underlying CPI, ulc is a measure of unit labour costs, and pm is import prices. Prices are modelled as a markup on unit labour costs and imported goods prices. The restriction that the coefficients on prices, unit labour costs and import prices sum to zero was imposed.
Unit Labour Costs
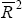 = 0.221 = 0.221
|
Standard Error = 0.010 |
| Jarque-Bera test: 0.368[p=0.83] | LM(4) Test: 0.57 [p=0.68] |
| Durbin-Watson = 2.32 |
The unit labour cost equation is a linear Phillips Curve incorporating adaptive expectations. The assumption of adaptive expectations has historically provided the best fit for Australian data. The equation was estimated with the restriction that the coefficients on lagged inflation sum to one. This restriction is not rejected by the data. The final term in the equation captures ‘speed-limit’ effects. That is, the speed with which the output gap is closed also affects wage pressures in addition to the size of the gap itself.
Import Prices
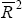 = 0.798 = 0.798
|
Standard Error = 0.015 |
| Jarque-Bera test: 2.22 [p=0.33] | LM(4) Test: 0.42 [p=0.79] |
| Durbin-Watson = 1.75 |
where e is the nominal exchange rate. We assume unitary pass-through of movements in the exchange rate in the long-run and that world prices are zero.
Real Exchange Rate
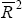 = 0.537 = 0.537
|
Standard Error = 0.031 |
| Jarque-Bera test: 1.64 [p=0.44] | LM(4) Test: 1.25 [p=0.30] |
| Durbin-Watson = 1.78 |
where rer is the real exchange rate, measured using the real trade weighted index, tot is the terms of trade and cpsdr is the commodity price index measured in SDRs.
Exogenous variables
Potential Output
where tot* is the steady state level of the terms of trade, rer* is the steady state level of the real exchange rate and yUS is the level of US real output.
For other exogenous variables, we assume:
Terms of Trade
Δtott = 0
Commodity Prices
Δcpsdrt = 0
US Real Output
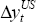 = 0.00625
= 0.00625
Nominal Exchange Rate
Assuming foreign inflation is zero:
Δet = Δrert − Δpt