RDP 2000-07: The Effect of Uncertainty on Monetary Policy: How Good are the Brakes? 2. Facts and Theories of Smoothing
October 2000
- Download the Paper 278KB
2.1 Facts
The path of short-term interest rates that results from the monetary policy decisions of most industrial-country central banks tends to be smooth. Table 1 documents the fact that central banks tend to change their policy settings relatively infrequently and in small steps.[1] The table also shows that policy changes in the same direction as the previous change are more common than policy reversals, and that there tend to be relatively long periods of inaction prior to a reversal.[2] The smooth path of policy interest rates that underpins Table 1 is illustrated in Figure 1.
| Country |
Number of changes |
Average number of days between changes | Average size of change in basis points | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Continuations | Reversals | All | Continuations | Reversals | All | Continuations | Reversals | |||
| Australia | 16 | 3 | 168 | 117 | 438 | 57 | 58 | 50 | ||
| US | 18 | 5 | 133 | 67 | 374 | 33 | 35 | 25 | ||
| UK | 27 | 5 | 96 | 81 | 179 | 41 | 43 | 30 | ||
| Germany/Euro area | 84 | 10 | 33 | 22 | 123 | 11 | 10 | 20 | ||
| Japan | 8 | 1 | 350 | 326 | 546 | 50 | 63 | 23 | ||
| Sweden | 50 | 5 | 48 | 33 | 195 | 27 | 27 | 28 | ||
| Canada | 36 | 5 | 52 | 42 | 123 | 34 | 35 | 25 | ||
Sources: Australia: cash rate Note: (a) Except Sweden (since December 1992) and Canada (since July 1994) |
||||||||||
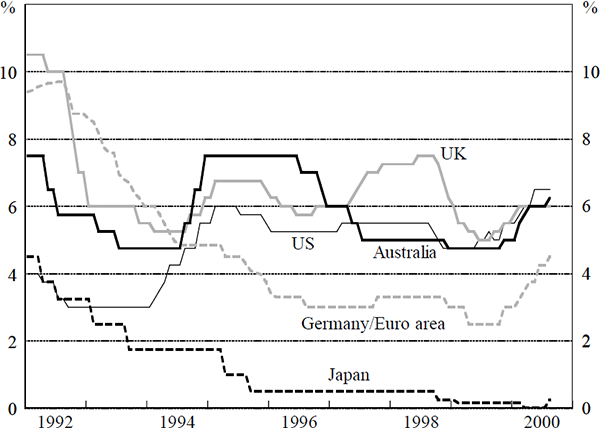
In considering whether these paths of policy interest rates are smooth, it is necessary to consider what the appropriate benchmark is. In the literature to date, two benchmarks have been proposed. Firstly, the observed pattern of policy interest rates has been compared to the optimal policy path derived from a macroeconomic model of the economy, where the policy-maker has the standard objective function that does not include an interest rate smoothing term.
This benchmark may be misleading because it ignores the effect of other information available to the policy-maker that is not captured in the model. For example, the model captures the average performance of the economy in history, whereas at any point in time, the policy-maker may consider that it has some knowledge about the residuals of the equations in the model, particularly with regard to future exogenous shocks. Even so, this does not explain the relative frequency of continuations and reversals; that is, the high degree of autocorrelation of policy interest rates.
A second benchmark that is used is the path of interest rates derived from a policy rule, generally a Taylor-type rule. In small closed-economy macro models (such as that in Svensson (1997)), the Taylor rule and optimal policy are equivalent, because all the state variables are in the rule. However, in larger models, the Taylor rule provides only an approximation to the path of interest rates derived from optimising the model, and certainty equivalence does not apply (Orphanides 1998).
To reconcile the differences between the degree of interest rate smoothing in theory and practice, one approach that has been commonly adopted is to simply impose interest rate smoothing on the model. This can be done by including a lagged interest rate term in a Taylor-type rule or by including the variance of interest rate changes in the policy-maker's objective function. While such modifications reduce the variability of interest rates, they do not explain the observed autocorrelation of policy changes. These modifications are also somewhat unsatisfactory as they are ad hoc (although Woodford (1999) derives a rationale for interest rate smoothing from first principles). Consequently in this paper, we try to identify more explicitly the factors that might induce less aggressive policy changes in practice, focusing primarily on uncertainty.
2.2 Theories
Eijffinger, Schalling and Verhagen (1999) break down the above pattern of behaviour into two facets. Firstly, they describe as interest rate ‘stepping’ the fact that policy interest rates are adjusted in discrete steps rather than continuously, despite new policy-relevant information arriving almost constantly.[3] Secondly, they describe smoothing as the process whereby policy is adjusted only gradually towards the desired position. For much of this paper, the term interest rate smoothing will encompass both forms of behaviour.
Lowe and Ellis (1997) discuss three possible explanations for this pattern of interest rate smoothing.[4] Firstly, smooth changes in policy interest rates may have the maximum effect on long-term interest rates. This argument was made by Goodfriend (1991) and is developed more theoretically by Woodford (1999). Goodfriend argues that the central bank is able to communicate its intentions more clearly to participants in the market by generating a smooth path of short-term interest rates, thereby allowing participants to infer future policy actions and build them into the long rates. The forward-looking behaviour of the market participants effectively undoes the smoothing behaviour of the policy-maker (Goodhart 1999). This suggests that a model that directly incorporates long-term interest rates and accurately reflects the expectations formation of market participants may generate a smoother optimal path for policy interest rates.
The relative infrequency of policy changes may increase the impact of the policy announcements when they actually occur. Lowe and Ellis (1997) provide some support for this hypothesis by finding that the effect of policy announcements on consumer sentiment in Australia is non-linear. That is, the announcement of the policy change itself has an effect on consumer sentiment, irrespective of the size of the change. They also find some evidence that the shift to explicit policy announcements in Australia in the early 1990s was associated with a larger impact on consumer sentiment than previously.
The second explanation for smoothing that Lowe and Ellis consider is that policy-makers may dislike frequent reversals in the path of policy interest rates because such behaviour might undermine public confidence in the monetary authorities and create instability in financial markets (Goodfriend 1987 and Cukierman 1996). For example, Goodhart (1999) cites a description of the Bank of England's recent behaviour (itself, far from the near random walk implied by economic models) as ‘almost laughable … like a drunk staggering from side to side down the street’. Moreover, the criticism(?) that the Monetary Policy Committee's actions were ‘fickle’, and ‘influenced by the latest anecdotal or statistical evidence, swaying its opinions one way or the other and back again’, would be an accurate description of the policy outcomes if the Monetary Policy Committee were to follow the dictates of an optimising macro model.
This rationale for smoothing is difficult to test because there have been few instances where central banks have pursued a policy that has resulted in volatile rates.[5] Nevertheless, to investigate this hypothesis, Lowe and Ellis (1997) examine whether long-term bond yields are more volatile around periods when there are policy reversals. They find that there is some evidence of increased volatility in Australia, the UK and the US, but that it is generally short-lived. However, if central banks were to move to a regime where reversals were more commonplace, volatility may decline. This would particularly be the case if financial market participants had a good understanding of the central bank's reaction function.
The third explanation is that the nature of the monetary-policy decision process requires that the central bank build a consensus before a change in interest rates can be adopted (Goodhart 1996). As the evidence to defend a particular action may often only accumulate slowly, so the consensus-building process may also be drawn out. This may be particularly the case where the monetary policy decision is taken by a committee rather than by a single policy-maker (Blinder 1995b).
More formally, the infrequency of policy changes can also be motivated by Dixit-Pindyck uncertainty considerations. If there are costs in implementing policy changes, then in an uncertain world, there is an option value to waiting and not reacting to each piece of economic information as it comes to hand (Eijffinger et al 1999).
Nevertheless, if the policy-maker(s) were to take the evidence of the economic model at face value, that should be sufficient to justify a policy decision. The fact that this doesn't occur suggests that the economic models are lacking some critical ingredients, or that central banks are behaving sub-optimally. In the next section, we discuss the ingredient of uncertainty.
Footnotes
Note that the table refers to nominal, rather than real rates. While the former are generally the policy instrument of central banks, the latter are often the instrument of monetary policy in empirical models including the one used in this paper. If inflation and inflation expectations change sluggishly, this distinction will not greatly affect the comparison of theory and practice. [1]
Rudebusch (1995) documents the pattern of changes in the Fed funds rate in the United States in more detail and estimates hazard functions for continuations and reversals. [2]
Conventionally, the decision-making bodies of most central banks meet at most once a month, thereby providing a bound on the frequency of policy changes. Multiple inter-meeting policy changes are extremely rare. [3]
There are other strands of literature that consider smoothing in terms of the seasonal movements in interest rates (Mankiw and Miron 1991), and in terms of the optimal inflation tax (Mankiw 1987 and Barro 1989) which will not be discussed here. [4]
The disinflation in the United States in the early 1980s is one such period, although the instrument of monetary policy at the time was non-borrowed reserves rather than a short-term interest rate. Interestingly, Mayer (1999) cites fears of generating instability in financial markets as a possible explanation for ‘excessive’ smoothing by the Fed in the 1970s. [5]