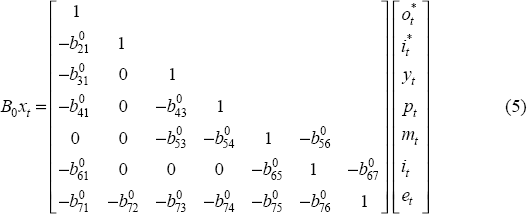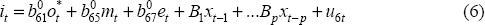RDP 1999-11: A Structural Vector Autoregression Model of Monetary Policy in Australia 2. Monetary SVAR Models

2.1 SVAR Framework

The estimation structure is as follows.^[5] Let x_t be an n × 1 vector of variables and u_t be an n× 1 vector of mean zero structural innovations. For simplicity of presentation, we ignore any constant terms in the model. The p^th order structural VAR model is written as:

for t = −(p−1)…T. We condition on the first p observations, x_−p+1…x₀. B(L) is a p^th order matrix polynomial in the lag operator L, B(L)= B₀−B₁L−B₂L²−…−B_pL^p. B₀ is a non-singular matrix and is normalised to have ones on the diagonal. This matrix summarises the contemporaneous relationships between the variables of the model and is most commonly where identification restrictions are imposed.

Associated with the structural model is the reduced form VAR representation:

where 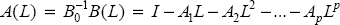and .

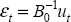To estimate the structural VAR model requires that the model be either exactly identified or over-identified. A necessary condition for the model to be exactly identified is that there must be the same number of parameters in B₀ and D as there are in Σ, the covariance matrix from the reduced form. In other words, it must be possible to recover the structural parameters from the reduced form model. (This is the order condition. The model must also satisfy the rank condition that is more difficult to verify. We assume that this condition is met. For further discussion, see Hamilton (1994).)

From the above, the relationship between the reduced form and the structural model can be expressed as:

Exact identification requires that the parameters in B₀ and D, of which there are 2n²−n, be uniquely recoverable from the reduced form. Since Σ has n(n+1)/2 parameters, we require 2n²−n−n(n+1)/2 restrictions on B₀ and D. It is standard in the SVAR literature to restrict D to be diagonal, imposing n(n−1) restrictions.^[6] We require a further n(n−1)/2 restrictions on B₀. For example, this can be accomplished by assuming that B₀ is lower triangular; this is the standard recursive or Wold causal ordering often employed in SVAR studies.

For an exactly identified model with no restrictions on A_j, a simple two-step maximum likelihood estimation procedure can be employed, assuming the structural errors are jointly normal. This is the FIML estimator for the SVAR model.^[7] First, Σ is estimated as 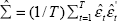, where 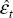are the OLS residuals from each equation of the reduced form model. Estimates of B₀ and D are then obtained by maximising the log likelihood for the system conditional on 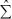. This amounts to finding the solution to the system of non-linear equations given in Equation (3).

When the model is over-identified, however, the two-step procedure is not the FIML estimator for the SVAR model. The estimates are consistent but not efficient (see the discussion in Judge et al (1985, p. 619)) since they do not take the over-identification restrictions into account when estimating the reduced form. Nevertheless, this is a common means to estimate these models, for example Sims (1986), Gordon and Leeper (1994) and Kim and Roubini (1999), and it is the method we use here.^[8]

Ideally, the restrictions imposed to identify a SVAR model would result from a fully specified macroeconomic model. In practice, however, this is rarely done. (Gali (1992), Garratt et al (1998), Huh (1999) and, to a lesser extent, Sims and Zha (1998a) are studies that go some way toward this ideal.) Instead, the more common approach is to impose a set of identification restrictions that are broadly consistent with economic theory and provide sensible outcomes. Generally, the metric used is whether the behaviour of the dynamic responses of the model accords with economic theories.

Leeper, Sims and Zha (1996), LSZ, provide a defence of this approach, representing it as an informal means of applying more formal prior beliefs to the econometric modelling. They argue persuasively that such an approach is in principle no different from other specification methods used in modelling – as long as the modeller does not fail to disclose the methods used to select the model. In particular, they argue that specifications consistent with any reasonable economic theory should not be dismissed in favour of a specification that accords with the modeller's own prior beliefs. Nonetheless, there are still legitimate concerns about SVAR models and the identification restrictions that have been employed in the literature. One important issue is the robustness of the conclusions to alternative reasonable identification restrictions, see Faust (1998). Uhlig (1997) has raised a further issue concerning the approach advocated by LSZ. He argues that in most instances of VAR modelling, it is too difficult to document completely the model specification process undertaken making it unclear what aspects of the model arise from criteria imposed on the model and what arise from the data.^[9]

These concerns are clearly important and provide a motivation for considering an existing structure that has proved successful, in some directions, for other countries. We can reasonably argue that the model has not been tailored in unspecified directions to provide desired responses for the Australian data. Of course, this does not provide any assurance that the identification structure is in some sense ‘correct’ or that our conclusions are not sensitive to the identification restrictions imposed. It merely makes our approach more transparent.

Given a set of variables of interest and criteria for model selection, identification restrictions can be imposed in a number of different ways. Most commonly, these involve restrictions on B⁰, 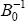or long-run restrictions imposed on B(1).^[10] The KR model, consistent with much of the SVAR literature, imposes restrictions only on the B₀ matrix, the contemporaneous relationship between the variables of the system. Generally, restrictions on B₀ are motivated in one of the following ways.

First, with open economy models, it is common to identify an external sector that does not respond contemporaneously to movements in domestic variables so that the B₀ matrix is block triangular. (This can be extended further by restricting the whole of B(L) to be block triangular as in Cushman and Zha (1997) and Dungey and Pagan (1998).) The second argument used to justify identification restrictions on the B₀ matrix is the timing of information. If we think of an equation of the SVAR model as a behavioural equation, a policy response function for example, then we can impose zero restrictions based on the fact that certain variables are only available with a lag. For example, an output measure for time t is only available after one quarter, at time t + 1.^[11]

A third type of argument is the imposition of behavioural assumptions. For example, KR imposes the restriction that domestic monetary authorities do not respond contemporaneously to movements in foreign interest rates. A further type of behavioural restriction often imposed is that certain variables respond slowly to movements in financial and policy variables. So, for example, output and prices do not respond contemporaneously to changes in domestic monetary policy variables.

2.2 The Kim and Roubini Model

The model specified by Kim and Roubini considers the following set of variables:

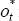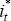where all variables except interest rates are expressed in logarithms. is an oil price index in current US dollars, the Federal Funds rate, y_t is domestic output, p_t the domestic price level, m_t a narrow monetary aggregate, i_t the domestic policy interest rate and e_t the exchange rate expressed in US dollars.

The oil price variable is included to capture anticipated inflation for the G6 countries. It is generally accepted that these models require such a variable in order to account for forward-looking monetary policy. Typically, we observe interest rates rising in advance of measured inflation. Without specifying the response of policy-makers to anticipated inflation, these models predict that an innovation to monetary policy leads to a rise in the price level (or inflation, depending upon the specification) – this is the price puzzle. KR includes the oil price index to resolve the price puzzle.

The Federal Funds rate is included to control for the response of domestic monetary policy to US financial variables. KR cites evidence in Grilli and Roubini (1995) that this is important for the G6 countries. For the sample we consider, Australia has had relatively open capital markets and it is also reasonable to assume that domestic interest rates are related to US interest rates.

The remaining variables are simply the standard variables of open economy monetary business cycle models: output, price, money, an interest rate, and the exchange rate. One point to note, however, is the focus on US interest rates and the USD exchange rate. This means that the US is serving as a proxy for the international economy. While this might not be ideal for all purposes, it has the advantage of being simple. Further, there is sufficient evidence to suggest that the US has an important influence on Australian financial variables and is likely to act as a reasonable proxy. (See de Roos and Russell (1996) and Dungey and Pagan (1998).)

The KR model restricts the elements of the B₀ matrix as follows (with zeros above the diagonal suppressed):

Further, the structural variance covariance matrix D is assumed to be diagonal. The model is over-identified – there are five more restrictions than required to just identify the model. As well, written in this manner, it is easy to see that the model is largely recursive with the exception being the relationship between the domestic interest rate, the monetary aggregate and the nominal exchange rate.^[12] To make the notation of Equation (5) more explicit, it is useful to consider an individual equation of the model in complete detail. For example, the domestic interest rate equation is:

The other equations of the model can be similarly expanded.

The explanation for the restrictions imposed is as follows. The first two variables are treated as external variables which are unaffected by contemporaneous movements in any domestic variable. The Federal Funds rate, denoted 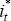, depends contemporaneously on the oil price variable reflecting the role this variable plays as a proxy for measures of anticipated inflation. Domestic output is assumed to respond to changes in oil prices immediately, as are domestic prices. This is based on the assumption that oil prices are an important determinant of production and pricing decisions and firms respond quickly to any changes.^[13] Otherwise, output is assumed to adjust slowly to the financial variables of the model. Similarly, the price level is assumed to adjust slowly to all variables except for movements in output (and oil prices as discussed).

The interest rate equation is interpreted as the policy reaction function of the central bank. The interest rate we use is the official cash rate, the interest rate in the overnight money market in Australia.^[14] The policy reaction function of the central bank depends contemporaneously on three variables: the oil price variable, the domestic monetary aggregate and the nominal exchange rate. The oil price variable is included as a proxy for anticipated inflation. The justification for excluding output and the price level is based upon the timing of information; that is, measures of these variables are not available at the time policy is set. For the price level, this is reasonable since we have included a variable to act as a measure of anticipated inflation. For output, however, one should be aware we are restricting the monetary authorities from responding to any indicators of future output apart from those specified in the model.

Finally, an important omission from the policy reaction function is the US interest rate. Kim and Roubini justify this by arguing that for domestic monetary authorities the information in changes to the Federal Funds rate, expected or unexpected, is dominated by the information in the movements of the nominal exchange rate. This contrasts with Cushman and Zha's model for Canada, which includes the US Federal Funds rate in the domestic policy reaction function. Cushman and Zha (1997) (CZ hereafter) argue that inclusion of this variable is important in specifying their model. To foreshadow our results, we find it necessary to follow CZ and include the contemporaneous US Federal Funds rate in the domestic interest rate equation in order to obtain sensible dynamic responses. This is also a source of difference between our model and Dungey and Pagan as the latter also exclude the foreign interest rate (contemporaneously) from their domestic interest rate equation.

The monetary aggregate equation is specified as a standard money demand equation, dependent upon output, prices and interest rates. We use a measure of M1, consistent with KR. One aspect of this specification is that we do not restrict 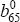=1 so that we would be modelling a demand for real balances (as, for example, CZ do). Were we to impose this restriction we would also have to consider how we wish to model the dynamic adjustment of money demand – in terms of nominal or real balances. For simplicity, we follow KR and leave the contemporaneous and dynamic relationships unrestricted with a possible loss of efficiency.

Finally, the exchange rate is treated as dependent upon all innovations of the model. This reflects the fact that the exchange rate is a financial variable and reacts quickly to all information. A similar argument is employed in CZ.

It is instructive to highlight the similarities between the KR model and the CZ model. Although the KR model is much smaller in dimension, the two models share, to a considerable extent, the same structure for money demand and supply. For money demand, the specifications are identical in terms of exclusion restrictions. The only difference is that the coefficients on m and p are restricted to be equal and opposite signs in CZ. The money supply or interest rate equation is also nearly identical in structure, the only difference being that CZ include the Federal Funds rate, as already mentioned. So, to summarise, both KR and CZ impose effectively the same non-recursive structure for the monetary components of the model.

As both papers provide models with reasonable dynamic responses for monetary policy innovations, it suggests that this non-recursive monetary structure is the important element of the identification scheme for each model. Some sensitivity analysis presented below confirms that this is the case for Australia. It further suggests that the additional restrictions imposed on the dynamics of the model by CZ so that the B(L) matrix is block triangular, are not crucial for identifying a reasonable model for a small open economy and, at least in the first instance, may be set aside.

Footnotes

A useful general reference for SVAR models is Hamilton (1994). [5]

Although it is standard to restrict D to be diagonal, it is not an innocuous restriction as it affects the interpretation of restrictions on B₀. [6]

This follows the discussion in Hamilton (1994, pp. 331–332). Hausman, Newey and Taylor (1987) generalise the estimation of simultaneous equations models with covariance restrictions beyond the normality assumptions underlying MLE. [7]

Two alternatives are to estimate the model using instrumental variables, as discussed in Pagan and Robertson (1998) or to use the Bayesian estimation method suggested by Sims and Zha (1998b) and Zha (1999). [8]

This is based upon the discussion in Faust (1998). [9]

Gali (1992) is an example of a model that uses all of these types of restrictions. Pagan and Robertson (1998) provide a discussion of the different type of restrictions used in SVAR models and some estimation issues; similarly, Faust and Leeper (1997) consider the usefulness of long-run identification restrictions. Finally, it is also possible to impose identification restrictions on the cointegration matrix of a VECM; see for example Garratt et al (1998) and Fung and Kasumovich (1998). [10]

The model must have sufficient dimension to warrant restrictions based upon the timing of information and a diagonal structural covariance matrix. For example, while inflation measures may only be available with a lag, a leading indicator of inflation may inform monetary policy. In this case, the exclusion restrictions on B₀ coupled with the diagonal covariance matrix are not valid restrictions. Fundamentally, the problem is one of an omitted variable leading to a mis-specified model. [11]

We order the model differently to Kim and Roubini. We do so to identify the features of the model which make it differ from the more standard recursive ordering. For example, this model is very similar to the recursive model in Eichenbaum and Evans' (1995) study for the US which documents evidence of the exchange rate and forward discount puzzle. [12]

Notice that the oil price variable is measured in USD. Domestic producers, however, are more likely to be concerned with the AUD value. Consequently, these identification restrictions are likely to be too simple, not accounting for the interaction between the USD oil price and the exchange rate. This is a limitation of the KR structure. (We are grateful to Adrian Pagan for bringing this to our attention.) As it turns out that the oil price variable plays very little role in the model when applied to Australian data, we do not amend this aspect of the KR model. [13]

For the whole of the sample period we consider, this interest rate has been the principal policy instrument of the Reserve Bank. While reserve ratios were also used to some extent in the early part of the sample, the cash rate was still an important policy instrument. For a more complete discussion of these issues, see Macfarlane (1984) and Rankin (1992). [14]