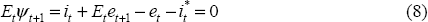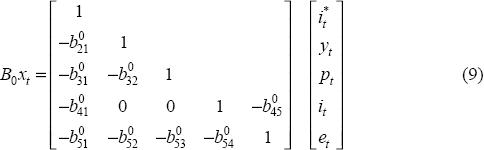RDP 1999-11: A Structural Vector Autoregression Model of Monetary Policy in Australia 3. Estimation Results
December 1999
- Download the Paper 819KB
3.1 Data
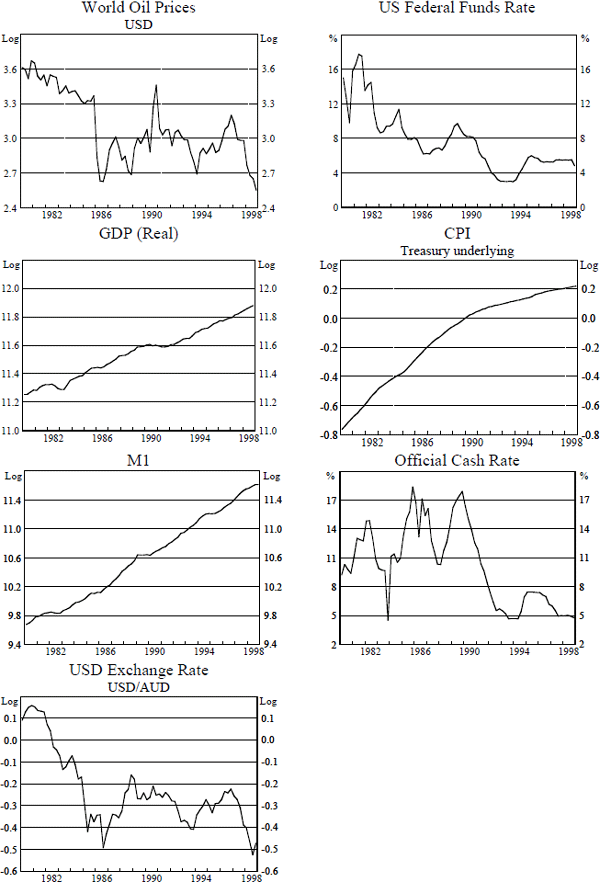
The data are quarterly for the sample period 1980:Q1–1998:Q4, 76 observations. All variables are in logarithms except for the interest rate variables, which are in annual terms. The foreign variables are a current USD spot price for oil and the US Federal Funds rate. The Australian variables are real GDP, the underlying consumer price index, a narrow monetary aggregate (M1), the official cash rate and the USD/AUD exchange rate. Full details on the data including source are available in the data appendix. Figure 1 presents the series as they are used in the estimation. This sample period is later than the sample periods considered in Kim and Roubini, which run from mid-1970 to mid-1990. For Australia, the later sample period we choose is more appropriate because of the structural changes, in particular financial market deregulation, that occurred during the late 1970s and early 1980s. Dungey and Pagan (1998) also focus on this later sample period for similar reasons.
3.2 Estimation
We estimate two versions of the Kim and Roubini model. The first is the one we have already
described and we refer to this as Model 1. The second allows the Federal Funds rate to enter the
interest rate equation contemporaneously; that is, we do not restrict 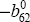 to be zero. We refer to this as Model 2.[15]
to be zero. We refer to this as Model 2.[15]
All models are estimated in levels. As some or all of the variables are possibly non-stationary in levels, it is possible that standard inference will not be correct, although the models estimated in levels should provide consistent parameter estimates. Further, if the variables are integrated then there may also be a set of cointegration restrictions that, if imposed, would improve the efficiency of the estimation.
We accept the loss of efficiency in preference to imposing possibly incorrect restrictions on the data resulting in a mis-specified model. Inference, however, is more troubling. While we do report likelihood ratio tests of over-identification restrictions, we cannot be confident of the distribution of these statistics. For the impulse response functions and the variance decompositions, we use the bootstrap procedure in Kilian (1998). An alternative and common approach is to use a Bayesian framework, as advocated by Sims and Zha (1998b) among others. This involves quite different methods of inference and we leave this for future work.[16]
The lag length for the reduced form model is set at p = 6, which is the maximum lag length that is feasible for our sample period. The choice of p = 6 is generally supported by the diagnostic tests reported in Table 1. For lag lengths less than six, using a conventional significance level of five per cent, we find evidence of first and fourth order serial correlation in the residuals of some of the equations of the VAR. With a lag length of six, only the residuals of the oil price equation exhibit any serial correlation at the five per cent significance level. A lag length of six is also supported by the ARCH tests, although there remains some evidence of ARCH(1) in the residuals of the domestic price and interest rate equations. Additional support is provided by the likelihood ratio tests for lag length where a lag length of five is strongly rejected in favour of the alternative of six. Finally, AIC and Schwarz criteria are presented for each lag length with the AIC criteria providing support for p = 6. Given the serial correlation and ARCH in the residuals for p = 4, 5 we ignore the Schwarz criteria supporting p = 4.
| Equation Diagnostics | Equation | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| p | ot* | it* | yt | pt | mt | it | et | ||
| Serial Correlation of Residuals | |||||||||
| AR(1) | F |
4 |
6.318 (0.016) | 0.516 (0.477) | 0.012 (0.913) | 0.436 (0.513) | 0.015 (0.903) | 0.577 (0.452) | 0.002 (0.964) |
| 5 |
4.755 (0.036) | 0.288 (0.595) | 0.055 (0.816) | 0.500 (0.485) | 6.734 (0.014) | 0.332 (0.568) | 0.081 (0.778) | ||
| 6 |
3.260 (0.083) | 0.042 (0.839) | 0.246 (0.624) | 0.153 (0.699) | 0.021 (0.887) | 0.496 (0.488) | 3.412 (0.076) | ||
| AR(4) | F |
4 |
1.983 (0.116) | 4.142 (0.007) | 1.482 (0.226) | 0.747 (0.566) | 1.824 (0.144) | 0.859 (0.497) | 2.726 (0.043) |
| 5 |
4.486 (0.006) | 2.842 (0.041) | 1.755 (0.163) | 1.148 (0.353) | 2.058 (0.111) | 0.819 (0.523) | 0.798 (0.536) | ||
| 6 |
3.839 (0.016) | 1.517 (0.230) | 2.507 (0.070) | 1.093 (0.383) | 1.160 (0.354) | 0.729 (0.581) | 1.310 (0.296) | ||
| Arch of Residuals | |||||||||
| ARCH(1) | χ2 (1) |
4 |
3.005 (0.083) | 0.754 (0.385) | 0.287 (0.592) | 5.686 (0.017) | 0.410 (0.522) | 5.615 (0.018) | 0.490 (0.484) |
| 5 |
3.957 (0.047) | 1.606 (0.205) | 0.001 (0.977) | 0.663 (0.416) | 0.046 (0.831) | 8.626 (0.003) | 0.130 (0.719) | ||
| 6 |
0.086 (0.769) | 1.073 (0.300) | 0.285 (0.594) | 3.859 (0.049) | 0.024 (0.876) | 3.998 (0.046) | 0.002 (0.962) | ||
| ARCH(4) | χ2 (4) |
4 |
4.081 (0.395) | 12.215 (0.016) | 1.523 (0.823) | 5.647 (0.227) | 4.206 (0.379) | 6.801 (0.147) | 5.382 (0.250) |
| 5 |
7.098 (0.131) | 11.592 (0.021) | 1.350 (0.853) | 0.903 (0.924) | 1.453 (0.835) | 9.555 (0.049) | 3.595 (0.464) | ||
| 6 |
2.147 (0.709) | 5.761 (0.218) | 2.715 (0.607) | 5.135 (0.247) | 1.380 (0.848) | 4.408 (0.354) | 4.033 (0.402) | ||
| STABILITY (1993:3) | |||||||||
| χ2 (15) |
23.506 (0.074) | 27.014 (0.029) | 28.222 (0.020) | 26.550 (0.033) | 30.900 (0.009) | 23.573 (0.073) | 29.230 (0.015) | ||
| System Diagnostics | |||||||||
| p = 4 | p = 5 | p = 6 | |||||||
| AIC | −38.06 | −38.50 | −40.79 | ||||||
| Schwarz Criterion | −31.64 | −30.47 | −31.12 | ||||||
| Lag Length | H0: p = 1 | H0: p = 2 | H0: p=3 | H0: p=4 | H0: p=5 | ||||
| H1: p = 2 | H1: p = 3 | H1: p=4 | H1: p=5 | H1: p=6 | |||||
| χ2 (49) |
61.172 (0.114) | 64.593 (0.067) | 62.985 (0.086) | 56.532 (0.214) | 93.158 (0.000) | ||||
|
Notes: Sample is 1980:1–1998:4. Marginal significance levels are in parentheses. The test for serial correlation is from Davidson and Mackinnon (1993, p. 359). The degrees of freedom for this test are (r,n−(pk+1)−r) where r is the degree of serial correlation, n the number of observations and k the number of variables in the VAR. The test for ARCH is from Davidson and Mackinnon (1993, p. 557). The test for lag length is the LR test described in Hamilton (1994, p. 297). The stability test is a heteroskedasticity robust Chow-type test as described in Davidson and Mackinon (1993, p. 378) |
|||||||||
We present this aspect of the model specification with some care for two reasons. First, it turns out that the structural estimation is sensitive to the choice of lag length. We obtain very different results for p = 6 relative to the results for p = 5 for Model 2 (our preferred model, as we explain below). It is necessary then, for the results to be credible, that p = 6 be a suitable choice. The second reason to be careful is that the bootstrap procedure we employ for inference, due to Kilian (1998), assumes that the residuals of the VAR model are independent and identically distributed.
The results for Model 1 are summarised in Table 2 and Figure 2. Table 2 presents the estimate of B0, the associated standard errors and a likelihood ratio test of the over-identification restrictions. While we cannot reject the over-identification restrictions at standard significance levels, the marginal significance level is quite low, 0.07, suggesting that the KR model may not be consistent with the Australian data.
| ot* | it* | yt | pt | mt | it | et | |
|---|---|---|---|---|---|---|---|
| 1 |
|||||||
| −0.0088 (0.0000) | 1 |
||||||
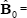 |
0.0123 (0.0109) | 0 |
1 |
||||
| 0.0029 (0.0039) | 0 |
−0.0581 (0.0425) | 1 |
||||
| 0 |
0 |
−0.3916 (0.2755) | 0.0149 (0.4973) | 1 |
0.2480 (0.3117) | ||
| 0.0003 (0.0273) | 0 |
0 |
0 |
0.5878 (0.3366) | 1 |
−0.3270 (0.1862) | |
| 0.0059 (0.0959) | −8.3393 (3.1696) | 1.0616 (1.9125) | −3.3730 (3.6756) | −0.4423 (1.6192) | 3.5693 (2.1353) | 1 |
|
| Test for Over-identification Restrictions χ2(5) 10.1741 (0.0705) | |||||||
|
Notes: Sample is 1980:1–1998:4. Standard errors from the ML estimation are reported in parentheses. The test for over-identification is a LR test, see Davidson and Mackinon (1993, p. 642). The marginal significance level is in parentheses. |
|||||||
Notes: These graphs show point estimates and 90 per cent confidence intervals of the responses of domestic variables over the following 24 quarters to a 25 basis point rise in the cash rate in quarter 1. After the initial 25 basis point increase, the cash rate responds endogenously to the system. All variables are in logarithms except for the interest rate which is in percentage terms. Note that a change of 0.01 in the log level of a variable is approximately equal to a one per cent change in that variable. Variables are y, domestic output, p, the underlying consumer price index, i, the domestic cash rate and e the USD/AUD exchange rate.
Figure 2 presents the estimated impulse response functions of the domestic variables (excluding mt which is not necessary for the following arguments) to innovations to it which result in an impact of 0.25 per cent.[17] For each point estimate, we also report a 90 per cent confidence interval generated by the bootstrap method described in Kilian (1998).[18] As is evident from Figure 2 (and Figure 3), these bands are very wide and in almost all cases encompass zero for the whole of the response. It is clearly important to provide these bounds to identify the uncertainty associated with the point estimates. We believe, however, that the focus should be on the point estimates, rather than the bounds themselves, as these provide the best guide to the model's responses. Throughout, the discussion will concern the point estimates and will note significance only, insignificance being the norm.[19]
An inspection of these impulse response functions indicates, however, that this model is not a
satisfactory description of monetary policy. Specifically, in response to an increase in the
cash rate of 0.25 per cent, we observe a rise in output and the price level and a depreciation
of the nominal exchange rate, all of which are inconsistent with what we expect to be the
effects of a contraction in monetary policy. On this basis and the results from the test of the
over-identification restrictions, we argue that the model has not accurately identified monetary
policy and we consider Model 2, which relaxes the restriction that  be zero.
be zero.
Table 3 and Figures 3a–d provide a summary of Model 2. The estimate of B0, the associated standard errors and the test of the over-identification restrictions are reported in Table 3. As before, we cannot reject the over-identification restrictions but this time with much greater confidence. The marginal significance level is 0.75. One notable feature of the results is the relatively large standard errors on the coefficients in the B0 matrix. Large standard errors are common in these models, see for example Sims and Zha (1998a) and KR, and in part underlie the uncertainty associated with the impulse response functions.[20]
| ot* | it* | yt | pt | mt | it | et | |
|---|---|---|---|---|---|---|---|
| 1 |
|||||||
| −0.0088 (0.0000) | 1 |
||||||
 |
0.0123 (0.0109) | 0 |
1 |
||||
| 0.0029 (0.0039) | 0 |
−0.0581 (0.0425) | 1 |
||||
| 0 |
0 |
−0.2448 (0.1978) | −0.1893 (0.5009) | 1 |
0.4571 (0.1394) | ||
| 0.0032 (0.0724) | −6.2416 (5.4021) | 0 |
0 |
−1.4029 (1.5268) | 1 |
1.1198 (1.1921) | |
| 0.0145 (0.1619) | 4.9730 (8.7254) | −5.8721 (4.5255) | 8.7294 (9.0767) | 0.0971 (0.8511) | −7.6258 (7.2145) | 1 |
|
| Test for Over-identification Restrictions χ2(4) 1.9205 (0.7504) | |||||||
|
Notes: See Table 2. |
|||||||
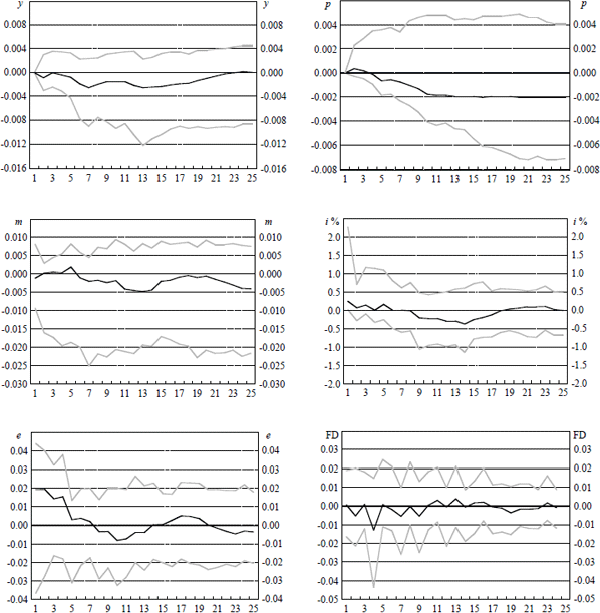
Notes: These graphs show point estimates and 90 per cent confidence intervals of the responses of domestic variables over the following 24 quarters to a 25 basis point rise in the cash rate in quarter 1. After the initial 25 basis point increase, the cash rate responds endogenously to the system. All variables are in logarithms except for the interest rate which is in percentage terms. Variables are y, domestic output, p, the underlying consumer price index, m, the monetary aggregate M1, i, the domestic cash rate, e, the USD/AUD exchange rate and FD the forward discount bias.
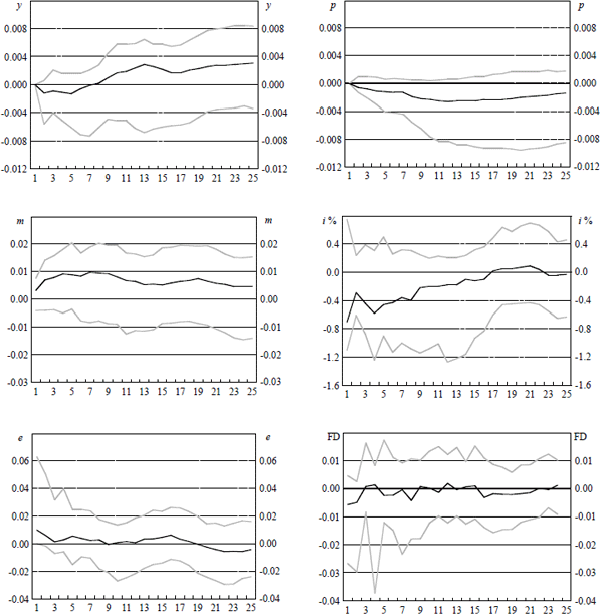
Notes: These graphs show point estimates and 90 per cent confidence intervals of the responses of domestic variables over the following 24 quarters to an increase of approximately one per cent in the exchange rate in quarter 1. After the initial increase, the exchange rate responds endogenously to the system. All variables are in logarithms except for the interest rate, which is in percentage terms. Variables are y, domestic output, p, the underlying consumer price index, m, the monetary aggregate M1, i, the domestic cash rate, e, the USD/AUD exchange rate and FD the forward discount bias.
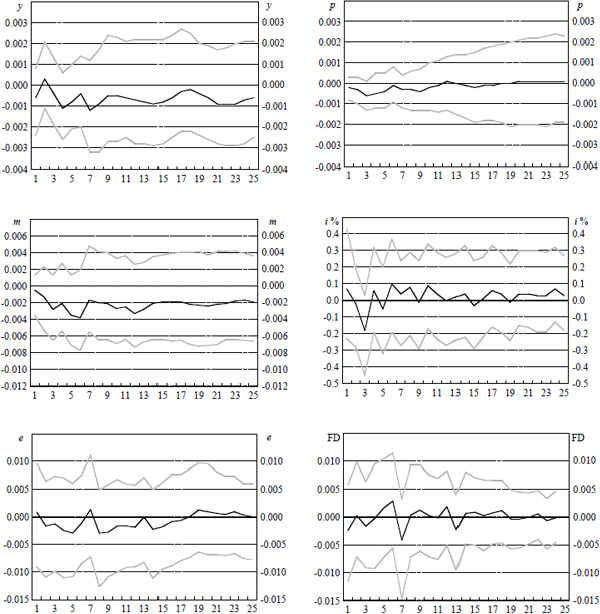
Notes: These graphs show point estimates and 90 per cent confidence intervals of the responses of domestic variables over the following 24 quarters to an increase of approximately five per cent in the oil price index in quarter 1. After the initial increase, the oil price responds endogenously to the system. All variables are in logarithms except for the interest rate which is in percentage terms. Variables are y, domestic output, p, the underlying consumer price index, m, the monetary aggregate M1, i, the domestic cash rate, e, the USD/AUD exchange rate and FD the forward discount bias.
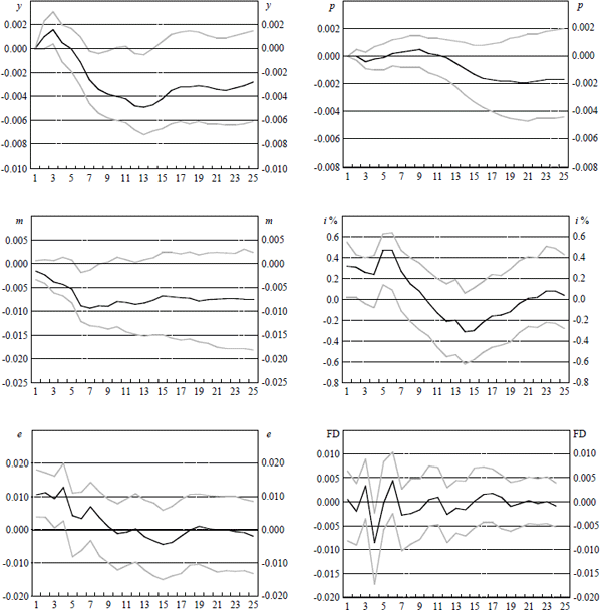
Notes: These graphs show point estimates and 90 per cent confidence intervals of the responses of domestic variables over the following 24 quarters to a 27 basis point rise in the Federal Funds rate in quarter 1. After the initial increase, the Federal Funds rate responds endogenously to the system. All variables are in logarithms except for the interest rate which is in percentage terms. Variables are y, domestic output, p, the underlying consumer price index, m, the monetary aggregate M1, i, the domestic cash rate, e, the USD/AUD exchange rate and FD the forward discount bias.
The estimated impulse response functions for the model are presented in Figures 3a–d and in contrast to Model 1, we obtain results that accord with our expectations and are broadly consistent with those of KR. We now consider these responses in detail with particular attention to the response of the economy to monetary policy innovations.
3.2.1 Innovations to the cash rate
Figure 3a presents the effects on the domestic variables of a one-off rise in the cash rate of 0.25 per cent. Before considering the effects of this rise, notice that the direct effect of the innovation on it itself is presented with standard error bounds. This arises because of the interdependence of the interest rate, money aggregate and the nominal exchange rate and the fact that the coefficients are estimated with error.
The contraction of monetary policy has the following effects. The level of output falls by about 0.20 per cent between 5 and 15 quarters after the contraction. After approximately 20 quarters the decline in output has been fully reversed. It appears that the long-run effects on output are very small or non-existent (although recall that the model estimated in levels may be biased against non-zero long-run effects, see Gali (1998)). The price level also falls with some delay with maximum effect, about 0.20 per cent by approximately 10 quarters. Unlike output, there is an indication that the effect on the price level may be permanent. As well, the effect on the nominal exchange rate is as we would anticipate – we see an immediate appreciation which lasts for roughly five quarters. This appreciation raises the USD/AUD exchange rate by 2.1 per cent above the value it would have otherwise been. After roughly two years the rate returns to its original level and it appears there are no permanent effects, although it does oscillate around zero. A feature of our results is the relatively small effects of monetary policy innovations on output and the price level and the quite large effects on the nominal exchange rate. This is similar to KR and to other monetary SVAR studies.
The permanent fall in the price level and the apparent transitory effect on the nominal exchange rate seems to suggest that we observe a permanent depreciation of the real exchange rate. The model does not, however, provide enough information to support this conclusion since the foreign price level is not included in the specification. It is not correct to argue that the foreign price level must remain unaffected by the domestic monetary innovation as identified in the KR model. This would only be true if we were confident that the innovation is not systematically correlated with movements in the foreign price level, something that is beyond the KR specification. KR addresses this to some extent by re-estimating the model with the real exchange rate in place of the nominal exchange rate.
Consistent with most of the exchange rate literature, they find that the two variables behave roughly the same — the nominal exchange rate response is similar to the real exchange rate response. We have also used the real exchange rate in the model and, similar to KR, the results are largely unchanged.[21]
The effect on M1 is not as well specified as we might wish. We do not observe a significant liquidity effect (fall in M1) in response to the contraction in monetary policy. We suspect that in order to examine the liquidity effect properly requires a much more detailed specification of the operation of monetary policy, along the lines of Bernanke and Mihov's (1998) study for the United States. This involves modelling a monetary aggregate much more closely related to the policy interest rate (in the US case, borrowed and non-borrowed reserves). The somewhat erratic response may also reflect the difficulties associated with modelling money demand in Australia (and elsewhere) due to instabilities arising from structural changes to financial markets over the sample period. (See de Brouwer, Ng and Subbaraman (1993).)
The results concerning monetary policy effects can be compared with previous work for Australia. We find that the effect on the level of output is largest between 5 and 15 quarters out. This is a similar lag length to the results reported in Dungey and Pagan (1998), although the magnitude of effects on output cannot be compared because Dungey and Pagan model responses around trend.
We now examine more closely the effects of a monetary policy innovation on the nominal exchange rate. For the United States, Eichenbaum and Evans (1995) identified an anomalous result: a persistent overshooting of the nominal exchange rate in response to an innovation to monetary policy. This overshooting results in excess returns to domestic assets and is referred to as the forward discount bias puzzle.
Excess returns are defined as:
The first three terms on the RHS are (approximately) the ex post return on domestic assets for one USD invested domestically (recall et is defined as the logarithm of the USD price of the domestic currency). If uncovered interest rate parity (UIP) holds, the conditional expectation of ψt is zero; that is:
The response of Etψt+1 is also plotted in Figure 3a. Although the uncertainty of the point estimates make it impossible to conclude with any confidence for or against the UIP hypothesis, there does appear to be some limited evidence of UIP being violated with excess returns mostly negative in the first nine quarters.[22] Further, the extent of the deviation is economically significant: the largest deviation is approximately −0.013 (i.e.−1.3 per cent) three quarters out. What is occurring is that after the initial appreciation, the subsequent depreciation more than offsets the difference between the domestic and foreign interest rate leading to the negative excess return. This result contrasts in two ways with those reported in Eichenbaum and Evans (1995). First, although we observe deviations from UIP we do not observe the same degree of persistence these authors identified for the United States. Second, Eichenbaum and Evans identified positive excess returns for US assets in response to a contraction in US monetary policy; in contrast, we observe negative excess returns for Australian assets in response to a contraction of Australian monetary policy. In effect, the model still exhibits a forward discount puzzle but in the opposite direction, a result in contrast to the conclusions of Kim and Roubini for the G6 economies.
3.2.2 Innovations to the nominal exchange rate
The responses of the domestic variables to a nominal exchange rate innovation are reported in Figure 3b. In response to an appreciation of approximately one per cent, the cash rate falls immediately by more than 0.50 per cent. This is consistent with monetary policy systematically moving to offset the price level effects following the appreciation. Even with this response, we still observe a smooth decline in the price level to a maximum decline of approximately 0.30 per cent after roughly 12 quarters. Interestingly, the long-run response of output to this innovation is positive. The level of output after 24 quarters is 0.25 per cent higher than it would have otherwise been. Two possible explanations can be offered. First, the exchange rate innovation may reflect innovations to the terms of trade. Alternatively, the results we observe could reflect the effect of the resultant reduction in the domestic interest rate. To fully examine this issue requires respecifying the model to include the terms of trade and successfully identifying both transitory and permanent terms of trade shocks. This is beyond the scope of the current study. We do, however, examine the role of monetary policy in response to nominal exchange rate shocks in further detail below when we consider alternative policy experiments.
3.2.3 Innovations to the oil price variable
Figure 3c presents the domestic variable responses to a one standard deviation innovation to the oil price index. These responses provide some useful information about the model and its suitability for Australian data. In particular, the response of the price level suggests that the oil price index is not acting as a leading indicator of inflation. Indeed, a positive oil price innovation leads to a fall in the price level, exactly the opposite of what we would expect were it playing this role. This result is not entirely unusual. Bernanke, Gertler and Watson (1997), which examines the effect of oil price shocks on the US economy in a model similar to that here, also finds that, for certain measures of oil prices, oil price shocks lead to a fall in the price level. These authors, whose focus is to model oil price shocks, resolve this by increasing the dimension of their model and using a more complicated measure of oil prices. Zha (1999) also examines this issue and demonstrates that the result is reversed if one treats this variable as exogenous to the system (that is B(L) has a block triangular structure). Finally, the result may reflect the fact that Australia is a net energy exporter with a floating exchange rate. Gruen and Dwyer (1995) argues that, with a floating exchange rate, a favourable terms of trade shock can in some instances be disinflationary. This depends upon the exchange rate appreciating in response to a terms of trade shock which lowers the price of importables. In terms of our results, this suggests that the oil price innovation may be interacting with the nominal exchange rate in such a way as to lead to a fall in the price level. (To further complicate matters, there is also the response of monetary policy affecting the results.) Whatever the source of the result, what is important for our current purposes is whether the oil price variable is acting as a leading indicator of inflation. The results in Figure 3c, coupled with the forecast error variance decompositions discussed below, suggest that it is not and one might wish to consider dropping this variable from the model.
3.2.4 Innovations to the foreign interest rate
Finally, Figure 3d reports the response of domestic variables to a rise in the foreign interest rate. In this case, the magnitude of the innovation is roughly 0.25 per cent, similar to the domestic monetary innovation. For output, prices and the domestic interest rate, we observe responses that are similar to a contraction in domestic monetary policy. This is generally consistent with KR's results for the G6 economies.
One should bear in mind, however, that we have a very limited specification of the external
sector. It is almost certainly the case that innovations to the Federal Funds rate in this model
cannot be interpreted as pure innovations to US monetary policy. Consequently, it would be
incorrect to interpret the coincident response of the domestic monetary policy instrument as the
domestic monetary authorities following US monetary policy. A more reasonable interpretation is
that innovations to 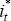 capture business cycle innovations in the US
and possibly the world economy. From this perspective, the response of domestic policy and
domestic variables seems understandable. This may also explain why the smaller dimension model
here, with a very limited description of the external sector, requires
capture business cycle innovations in the US
and possibly the world economy. From this perspective, the response of domestic policy and
domestic variables seems understandable. This may also explain why the smaller dimension model
here, with a very limited description of the external sector, requires 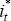 to be
included in the domestic interest rate equation. In contrast, Dungey and Pagan with a larger
external sector, need not include
to be
included in the domestic interest rate equation. In contrast, Dungey and Pagan with a larger
external sector, need not include 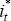 in the domestic interest rate
equation.[23]
in the domestic interest rate
equation.[23]
3.2.5 Forecast error variance decomposition
We now consider the forecast error variance decomposition for Model 2. In Table 4, we report the proportion of the forecast error variance of each variable accounted for by the innovations to each of the structural equations. Results are reported for forecast horizons 1, 4, 12 and 24 quarters ahead. As well, we report 90 per cent confidence intervals based upon the bootstrap procedure described earlier although, again, we focus discussion on the point estimates.
| Innovation | Forecast (quarters) | Proportion of forecast error variance for variable | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| yt | pt | it | mt | et | |||||||
| ot* | 1 | 0.02 | (0.00 0.24) | 0.01 | (0.00 0.20) | 0.01 | (0.00 0.22) | 0.00 | (0.00 0.18) | 0.00 | (0.00 0.16) |
| 4 | 0.02 | (0.01 0.18) | 0.04 | (0.01 0.22) | 0.02 | (0.02 0.23) | 0.03 | (0.00 0.24) | 0.00 | (0.01 0.15) | |
| 12 | 0.01 | (0.01 0.17) | 0.01 | (0.01 0.16) | 0.02 | (0.02 0.19) | 0.03 | (0.01 0.19) | 0.01 | (0.01 0.17) | |
| 24 | 0.01 | (0.01 0.16) | 0.00 | (0.00 0.14) | 0.01 | (0.02 0.17) | 0.02 | (0.01 0.16) | 0.01 | (0.02 0.17) | |
| it* | 1 | 0.00 | (0.00 0.00) | 0.00 | (0.00 0.00) | 0.13 | (0.00 0.36) | 0.04 | (0.00 0.20) | 0.16 | (0.02 0.37) |
| 4 | 0.04 | (0.01 0.19) | 0.01 | (0.00 0.10) | 0.18 | (0.03 0.32) | 0.08 | (0.00 0.21) | 0.20 | (0.05 0.39) | |
| 12 | 0.21 | (0.05 0.35) | 0.01 | (0.01 0.15) | 0.20 | (0.05 0.30) | 0.24 | (0.03 0.38) | 0.13 | (0.05 0.28) | |
| 24 | 0.23 | (0.04 0.37) | 0.07 | (0.01 0.32) | 0.20 | (0.06 0.30) | 0.23 | (0.03 0.35) | 0.10 | (0.05 0.26) | |
| yt | 1 | 0.98 | (0.75 1.00) | 0.03 | (0.00 0.21) | 0.08 | (0.00 0.25) | 0.09 | (0.00 0.31) | 0.03 | (0.00 0.21) |
| 4 | 0.71 | (0.36 0.77) | 0.01 | (0.01 0.18) | 0.04 | (0.03 0.23) | 0.32 | (0.09 0.53) | 0.04 | (0.01 0.21) | |
| 12 | 0.57 | (0.17 0.63) | 0.06 | (0.03 0.32) | 0.05 | (0.04 0.33) | 0.32 | (0.05 0.52) | 0.28 | (0.07 0.38) | |
| 24 | 0.53 | (0.11 0.60) | 0.32 | (0.03 0.52) | 0.10 | (0.06 0.36) | 0.45 | (0.06 0.58) | 0.30 | (0.09 0.40) | |
| pt | 1 | 0.00 | (0.00 0.00) | 0.96 | (0.65 0.99) | 0.03 | (0.00 0.13) | 0.00 | (0.00 0.09) | 0.00 | (0.00 0.08) |
| 4 | 0.16 | (0.02 0.34) | 0.82 | (0.41 0.83) | 0.04 | (0.01 0.16) | 0.01 | (0.01 0.14) | 0.10 | (0.02 0.28) | |
| 12 | 0.07 | (0.03 0.29) | 0.28 | (0.11 0.43) | 0.08 | (0.03 0.26) | 0.01 | (0.01 0.23) | 0.11 | (0.05 0.28) | |
| 24 | 0.06 | (0.02 0.34) | 0.11 | (0.03 0.34) | 0.09 | (0.04 0.28) | 0.01 | (0.02 0.29) | 0.15 | (0.05 0.31) | |
| mt | 1 | 0.00 | (0.00 0.00) | 0.00 | (0.00 0.00) | 0.01 | (0.00 0.55) | 0.64 | (0.13 0.88) | 0.06 | (0.00 0.17) |
| 4 | 0.02 | (0.00 0.14) | 0.00 | (0.00 0.14) | 0.03 | (0.01 0.48) | 0.16 | (0.03 0.47) | 0.03 | (0.01 0.14) | |
| 12 | 0.04 | (0.01 0.21) | 0.08 | (0.01 0.31) | 0.16 | (0.03 0.38) | 0.07 | (0.02 0.41) | 0.06 | (0.02 0.21) | |
| 24 | 0.02 | (0.01 0.24) | 0.15 | (0.01 0.40) | 0.14 | (0.03 0.36) | 0.04 | (0.02 0.37) | 0.10 | (0.03 0.27) | |
| it | 1 | 0.00 | (0.00 0.10) | 0.00 | (0.00 0.11) | 0.10 | (0.00 0.42) | 0.03 | (0.00 0.24) | 0.61 | (0.05 0.76) |
| 4 | 0.01 | (0.01 0.15) | 0.01 | (0.01 0.21) | 0.06 | (0.02 0.33) | 0.00 | (0.01 0.28) | 0.57 | (0.07 0.60) | |
| 12 | 0.07 | (0.01 0.23) | 0.18 | (0.02 0.45) | 0.09 | (0.04 0.30) | 0.03 | (0.01 0.31) | 0.36 | (0.07 0.45) | |
| 24 | 0.06 | (0.02 0.25) | 0.16 | (0.02 0.39) | 0.13 | (0.04 0.30) | 0.03 | (0.02 0.29) | 0.27 | (0.06 0.38) | |
| et | 1 | 0.00 | (0.00 0.00) | 0.00 | (0.00 0.00) | 0.64 | (0.00 0.43) | 0.19 | (0.01 0.75) | 0.14 | (0.01 0.59) |
| 4 | 0.04 | (0.01 0.18) | 0.11 | (0.01 0.28) | 0.63 | (0.03 0.51) | 0.40 | (0.05 0.63) | 0.06 | (0.02 0.42) | |
| 12 | 0.04 | (0.01 0.21) | 0.37 | (0.04 0.55) | 0.41 | (0.03 0.44) | 0.32 | (0.06 0.45) | 0.05 | (0.04 0.29) | |
| 24 | 0.09 | (0.02 0.27) | 0.19 | (0.03 0.52) | 0.32 | (0.03 0.42) | 0.22 | (0.06 0.39) | 0.07 | (0.04 0.28) | |
Notes: Numbers in parentheses are 90 per cent confidence intervals based upon the bootstrap procedure due to Kilian (1998). |
|||||||||||
The contributions of innovations to it, domestic monetary policy, are of the most interest and here we find results generally in keeping with the literature. Innovations to monetary policy contribute very little to the forecast error variance of output, contributing only approximately five per cent 24 quarters out. In other words, unanticipated changes to domestic monetary policy have very little effect on output. This is similar in magnitude (slightly smaller) to the results reported in the KR study for the G6 countries. It is also similar in magnitude to results reported in Dungey and Pagan which finds that the cash rate contributes between one and three per cent between 12 and 50 quarters out. Our results are also broadly consistent with the general findings from the SVAR literature – innovations to domestic monetary policy have very little effect on output. This is one of the principal conclusions Sims (1998) argues is robust to different model specifications.[24]
Also consistent with the US literature is the relatively small contribution of monetary policy innovations to the forecast error variance of the monetary policy instrument itself, in this case the interest rate. At most, innovations to it contribute roughly 15 per cent to the forecast error variance of it (after 24 quarters). In other words, most of the observed variation in monetary policy is endogenous – that is, a systematic response to the state of the economy, much as we would expect. This is similar to findings for US studies and is another conclusion from the SVAR literature that appears to be robust across model specifications (Sims 1998).
Where innovations to it do have a larger effect is on the exchange rate. In the short run, 60 per cent of the forecast error variance of et is explained by innovations to the domestic interest rate. And the contributions of 27 per cent are still substantial after 24 quarters. This is very similar to the results for Canada and Italy reported in KR while the other countries in the KR study have much smaller contributions. It confirms what we might have suspected – unanticipated movements in the domestic interest rate have substantial effects on the USD/AUD exchange rate.[25]
The variance decompositions also provide support for our previous concerns that the oil price variable is not particularly useful in the Australian context. Innovations to the oil price variable provide very little contribution to the variation of any of the domestic variables. Kim and Roubini also find little role for the oil price variable in their model for the UK and Canada. They argue that this reflects the fact that both of these countries are oil exporting countries so that changes in oil prices do not have the same effects as for the other countries. In response to this general result, they re-estimate the model for these countries, dropping the oil price variable, and obtain similar results.
The explanation put forward by Kim and Roubini, that this is a feature related to oil exporting countries, is less relevant for Australia since it has not been a consistent net exporter of petroleum products over the sample period.[26] Nonetheless, our results suggest that we can also estimate a six-variable model, one that excludes the oil price variable. The estimation results are reported in Table 5. Comparison of these estimates with those of Table 3 shows that the two models are broadly similar so, consistent with KR, we find little change in the conclusions. (For space considerations we do not present the impulse response functions. These are available upon request.)
| 6 Variable Model: eliminating the oil price variable | ||||||
|---|---|---|---|---|---|---|
| it* | yt | pt | mt | it | et | |
| 1 | ||||||
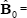 |
0 | 1 | ||||
| 0 | −0.0890 (0.0396) | 1 | ||||
| 0 |
−0.2239 (0.2693) | −0.2836 (0.6940) | 1 |
0.5734 (0.3342) | ||
| −5.4218 (3.5973) | 0 |
0 |
−0.8474 (0.7346) | 1 |
0.9934 (0.7874) | |
| 5.4668 (12.2161) | −7.6525 (8.4746) | 9.5933 (13.3456) | 4.1305 (6.4492) | −7.9373 (9.9259) | 1 |
|
| Test for Over-identification Restrictions χ2(3) 0.8813 (0.8299) | ||||||
| 5 Variable Model: eliminating the oil price and domestic monetary aggregate variables | ||||||
| it* | yt | pt | it | et | ||
| 1 | ||||||
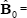 |
−0.0757 (0.1801) | 1 |
||||
| −0.0581 (0.0623) | −0.0822 (0.0412) | 1 |
||||
| −2.9459 (3.5313) | 0 |
0 |
1 |
0.7091 (1.2436) | ||
| 10.4249 (57.0075) | −3.0775 (12.7131) | 1.3609 (14.5768) | −13.3317 (57.7636) | 1 |
||
| Test for Over-identification Restrictions χ2(1) 0.4827 (0.4872) | ||||||
Notes: See Table 2. |
||||||
This result raises an interesting question, one not addressed by Kim and Roubini. If the oil price variable is not a necessary component of the model for the UK, Canada and (from our results) Australia, why then do we not observe evidence of the price puzzle? Recall that the role of the oil price variable is a leading indicator for inflation to capture forward-looking monetary policy actions. For the Australian data, three variables seem to be performing this role. Inspection of the reduced form equation for the price level reveals that the monetary aggregate, the cash rate and the nominal exchange rate are all useful predictors of the price level to some extent. In particular, the nominal exchange rate predicts the price level six periods ahead. This is consistent with the accepted view in Australia that nominal exchange rate movements feed through to the price level after some time. As noted previously, this is clearly evident in the response of the price level to a nominal exchange rate shock presented in Figure 3. This is not the complete story, however. As we discuss below, the non-recursive structure is also necessary to obtain a model with sensible results.
Finally, we also find support for our argument that the innovations to  are best
interpreted as external business cycle innovations. These innovations account for a substantial
proportion of variation in output and the domestic interest rate, much as we would anticipate
from a measure of external business cycle shocks. For example, innovations to US GDP and US
financial market variables in the Dungey and Pagan study make contributions of a similar
magnitude to domestic output. Further, of the countries in the KR study, only Canada, which is
closely linked to the US, has a contribution of
are best
interpreted as external business cycle innovations. These innovations account for a substantial
proportion of variation in output and the domestic interest rate, much as we would anticipate
from a measure of external business cycle shocks. For example, innovations to US GDP and US
financial market variables in the Dungey and Pagan study make contributions of a similar
magnitude to domestic output. Further, of the countries in the KR study, only Canada, which is
closely linked to the US, has a contribution of  to variation in
output of a similar magnitude to that here. This strong relationship between US and Australian
business cycles is also consistent with other empirical studies for Australia, see Gruen,
Romalis and Chandra (1997) for an overview.
to variation in
output of a similar magnitude to that here. This strong relationship between US and Australian
business cycles is also consistent with other empirical studies for Australia, see Gruen,
Romalis and Chandra (1997) for an overview.
3.3 Further Discussion
3.3.1 Alternative policy experiments
The previous section examines the effects of monetary policy by considering the effects of a one-off change in the structural innovations of the domestic interest rate equation. This procedure recognises the systematic component of monetary policy and uses deviations from an average policy reaction function to identify the effects of monetary policy. We can in addition consider other aspects of monetary policy. One possibility is to consider a sustained rather than a one-off change in the policy variable. A second possibility is to consider the role of systematic monetary policy in more detail by comparing the effects of innovations to the economy with and without the estimated response of monetary policy. Sims and Zha (1998a) present both of these types of experiments. Bernanke, Gertler and Watson (1997) consider the latter type, examining the effect of oil price shocks with and without an endogenous monetary policy response.
The simplest means of implementing these types of experiments is to replace the estimated policy reaction function, the interest rate equation, with one that is independent of the other variables of the model. For our purposes, we use a simple random walk model for the nominal interest rate. This means that all non-policy shocks have no effect on the domestic interest rate and one-off policy shocks have a permanent effect on the domestic interest rate.[27]
Since the model is not re-estimated when the random walk model replaces the policy reaction function, the underlying assumption is that the dynamics of the private sector are unaffected in the face of persistent deviations from the average policy rule. This assumption is susceptible to the Lucas critique. Sims and Zha accept this drawback and proceed. Bernanke, Gertler and Watson refine the procedure somewhat by allowing financial variables to adapt to the regime change while the real sector remains unchanged. This approximates the idea that financial market participants more quickly adapt to a change in policy regime relative to the rest of the economy. We follow Sims and Zha and treat the entire private sector in a uniform manner.
These alternative experiments are presented in Figure 4. Figure 4a presents the response of the domestic variables to two different policies: a sustained increase in the domestic interest rate of 0.25 per cent and a one-off innovation to the domestic interest rate of similar magnitude. (The latter experiment is the same as reported in Figures 3a–d and repeated here for comparison. For clarity, standard error bounds are omitted.) The permanent increase in the domestic interest rate has short-run effects similar to the one-off innovation. Output and price fall and the nominal exchange rate appreciates. In the case of the latter, the magnitude of the effect is somewhat larger in the case of the permanent shock; otherwise, the magnitudes are roughly the same. This suggests that over a policy horizon of four to eight quarters, the two policy experiments can be treated as effectively the same, particularly for price and output.
Notes: These graphs show point estimates of the responses of domestic variables over the following 24 quarters to changes in the cash rate of two types. The grey line shows responses to a sustained 25 basis point rise in the cash rate. The black line shows the responses to the standard VAR experiment where there is a 25 basis point rise in quarter 1, after which the cash rate responds endogenously to the system. All variables are in logarithms except for the interest rate which is in percentage terms. Variables are y, domestic output, p, the underlying consumer price index, m, the monetary aggregate M1, i, the domestic cash rate and e the USD/AUD exchange rate.
Where the responses of the two experiments differ is in the longer-run. After roughly two years, the permanent change in interest rates is associated with explosive paths for the other domestic variables of the model. We discount these long-run effects, however, as they involve substantial and accumulated deviations from historical behaviour on behalf of the central bank with no corresponding change in behaviour of the private sector.
Gruen, Romalis and Chandra (1997), although quite different in approach, presents results similar to those here. In their study, they find that a permanent increase in the real interest rate affects output significantly after three to four quarters but with the principal effects occurring after five quarters. After three to four quarters, the effect on the level of output in this study is a fall of 0.05 per cent.[28] Interestingly, we also find a decline in the level of output of 0.05 per cent after three quarters in response to a permanent increase in the nominal interest rate. After four quarters, however, our results diverge considerably with our model reporting an effect roughly four times as large as Gruen, Romalis and Chandra. At longer horizons our results diverge even further.
To better compare the two models, we can perform the following experiment. From our experiment, where we hold the nominal interest rate constant, we can obtain a path for the real interest rate calculated as the nominal interest rate less the four-quarter-ended log change in the price level. We can use the Gruen, Romalis and Chandra model to forecast the effect on output of this real interest rate path and compare this with that predicted by our model. After three quarters, the effect on the level of output is the same in both models. At longer horizons, the Gruen, Romalis and Chandra model has a much smaller impact on output than our model predicts.[29]
Figures 4b and 4c present the responses of the domestic variables to one-off innovations to the nominal exchange rate and the Federal Funds rate respectively under two policy scenarios. The first allows domestic monetary policy to respond according to the estimated endogenous policy response and the second restricts the interest rate response to zero.
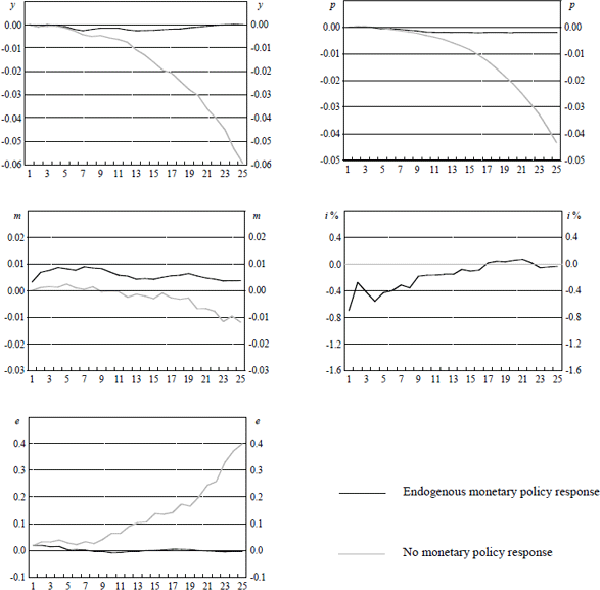
Notes: These graphs show point estimates of the responses of domestic variables over the following 24 quarters to a one per cent increase in the exchange rate. The grey line shows the responses of the variables when monetary policy does not respond endogenously to the system and the black line shows the responses when it does. All variables are in logarithms except for the interest rate which is in percentage terms. Variables are y, domestic output, p, the underlying consumer price index, m, the monetary aggregate M1, i, the domestic cash rate and e the USD/AUD exchange rate.
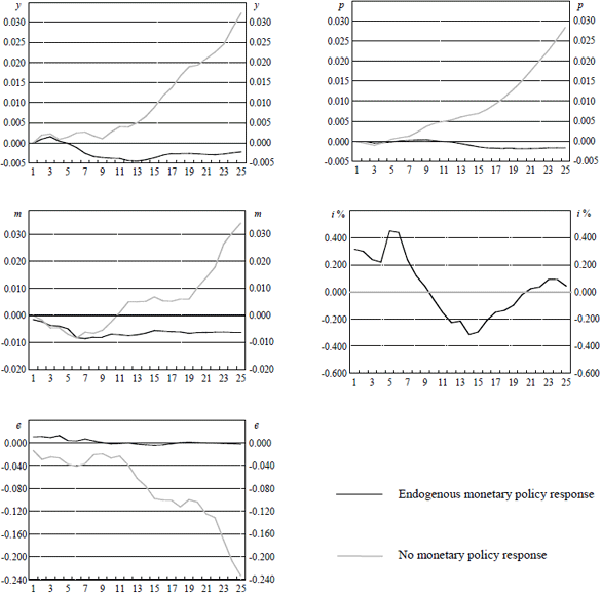
Notes: These graphs show point estimates of the responses of domestic variables over the following 24 quarters to a 27 basis point increase in the Federal Funds rate. The grey line shows the responses of the variables when monetary policy does not respond endogenously to the system and the black line shows the responses when it does. All variables are in logarithms except for the interest rate which is in percentage terms. Variables are y, domestic output, p, the underlying consumer price index, m, the monetary aggregate M1, i, the domestic cash rate and e the USD/AUD exchange rate.
For the exchange rate innovation, the estimated response of monetary policy is to offset the contractionary effect of the appreciation by lowering domestic interest rates. Relative to the no-response scenario, this has the effect of offsetting further persistent appreciation of the nominal exchange rate and consequent declines in the price level and the level of output. On the whole, it appears that monetary policy has on average stabilised the responses of the exchange rate, real output and the price level to exchange rate innovations.
For the Federal Funds rate innovation, roughly a 25 basis point rise, the estimated response of the domestic interest rate is a similar increase maintained over roughly the following eight quarters. Without this response, we observe a persistent and growing depreciation of the nominal exchange rate associated with an explosive increase in the price level and the level of real output. For reasons discussed previously, we probably wish to consider the relative effects over the short-run, discounting the longer-run effects. Over a horizon of four to eight quarters, what we observe is monetary policy offsetting the exchange rate depreciation induced by the Federal Funds rate rise. The explanation for this is either a direct desire to maintain stability of the exchange rate or to offset the subsequent effects on the price level, which occur after 8 to 12 quarters. The final outcome is for monetary policy to completely dampen the price level effect with some resultant fall in output.
Both these sets of results, the responses to exchange rate and foreign interest rate innovations, should be interpreted with some care. Innovations to the exchange rate and the Federal Funds rate are not fully identified within the model. In the case of the former, innovations may comprise terms of trade innovations or other external shocks which have an inflationary effect and, in our model, manifest themselves as exchange rate innovations. In the case of the US Federal Funds rate, innovations in this variable will capture movements in US monetary policy, US inflation and output shocks and possibly global business cycle shocks. These shocks, in our model, have an inflationary effect on the Australian economy and the Reserve Bank has, on average, moved against these shocks. Because of the model's limited external sector and the difficulty in identifying the nature of external shocks, we view these results as preliminary indicating that there is potential information in these types of experiments. A model sharing the basic features of the KR structure with a more fully developed external sector is likely to provide useful information about the role of monetary policy in Australia.
3.3.2 Stability
An important drawback of using monetary SVAR models to identify monetary policy is the need to treat the monetary policy reaction function, in our model the domestic interest rate equation, as a time invariant linear structure over the whole of the sample period under consideration. Rudebusch (1998a, 1998b) argues that this is an important weakness of many US studies and, given the data requirements of VAR studies, a weakness of the method in general. Recently, Bagliano and Favero (1997) document more completely the temporal instability of standard benchmark SVAR models for the US, finding strong evidence of instability for models estimated across policy regimes.[30]
The model we present above is estimated over the period 1980–1998, chosen to provide a reasonable number of observations while at the same time limiting the amount of structural change within the sample period. Nonetheless, the operation of monetary policy has undergone changes in this period and implicitly we have assumed that the model is robust to these changes. To examine this issue, we consider the stability of the model across two sub-samples, separated in mid 1993. This date can plausibly be regarded as the start of an explicit inflation-targeting regime for monetary policy.[31] While other important changes have occurred over the sample period, both to the structure of the Australian economy and the operation and objectives of monetary policy, the focus on the move to an explicit inflation target is clearly an important one. The usefulness of the model for current policy analysis depends to a large extent on it being a stable representation of the economy during the current policy regime.
Because we focus on structural change quite late in the sample, we do not have sufficient degrees of freedom to estimate the model over the two associated sub-samples. Consequently, we employ a procedure due to Chow (1960), outlined in Davidson and Mackinnon (1993), which allows us to consider break points without re-estimating over sub-samples.[32] The tests for structural break in mid 1993 are performed for each equation of the reduced form VAR model and are reported in Table 1. We perform the test on the reduced form since evidence of parameter instability in these equations must carry over into the structural model. From Table 1, we observe evidence of parameter instability in three equations: those for the foreign interest rate, the domestic interest rate and the monetary aggregate. At one level, this is further evidence of the difficulties of modelling monetary variables, in particular monetary aggregates.[33] More importantly for our purposes, these results imply that the monetary policy reaction function we specify is not robust to the change in monetary policy regime. While not too surprising, this is an important issue that subsequent research must deal with.
Although the stability tests indicate a problem with the specification of the model, it is difficult to know how important this is in economic terms since it is not possible to estimate a model with any confidence over the 1993–1998 period. Even with sufficient degrees of freedom, say using monthly data, there is still the issue that we observe less than one business cycle over the period. One limited means of further examining the instability is to re-estimate the model using subsets of the sample. Figure 5 reports the response of key domestic variables, output, price level, interest rate and exchange rate, to a monetary policy innovation. In terms of model specification, these responses are an important means of judging the structural model. Each figure shows three responses of a particular variable to an interest rate innovation. The three responses arise from three different sample periods all starting in 1980:Q1 but ending in 1996:Q4, 1997: Q4, and 1998:Q4 respectively.
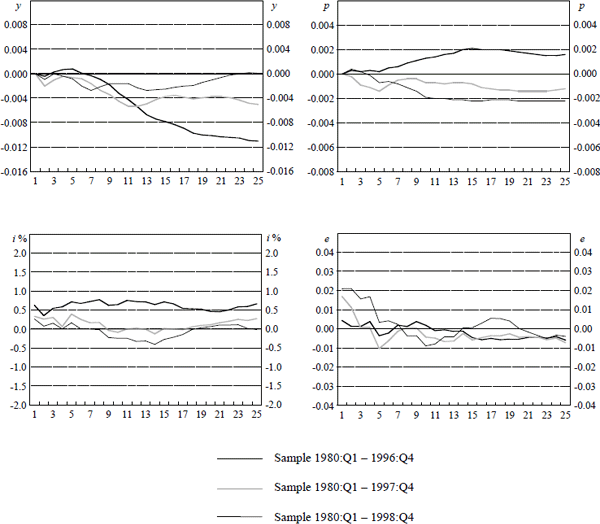
Notes: These graphs show point estimates for three different samples of the responses of domestic variables over the following 24 quarters to a one standard deviation rise in the cash rate in quarter 1. After the initial one standard deviation increase, the cash rate responds endogenously to the system. All variables are in logarithms except for the interest rate which is in percentage terms. Variables are y, domestic output, p, the underlying consumer price index, i, the domestic cash rate and e the USD/AUD exchange rate.
The broad features of the response of output appear to be relatively robust to these different sample periods, especially over the first couple of years, although it is only for the full sample that we observe output return to its original level. Similarly, the qualitative response of the nominal exchange rate appears to be robust to these different sample periods. The responses of the interest rate and price level, however, are more troubling. In the case of the former, the endogenous response of the interest rate to the state of the economy seems to be dependent upon the sample period. This supports the previous reduced form evidence that the interest rate equation is unstable. In the case of the price level, we have the most worrying result. The resolution of the price puzzle is not robust to different sample periods.
Clearly, instability is a problem with the model and this qualifies our conclusions. Nonetheless, we argue that the model still provides us with useful information, both about the effects of monetary policy and potential problems with these sorts of models. With respect to the former, despite the evidence of instability, our results are consistent with other studies in the literature, including Dungey and Pagan's study for Australia, and are broadly consistent with economic intuition. This suggests that we may be capturing important features of the Australian data. For the latter, the evidence we present here suggests that future work will need to address this instability directly.
3.3.3 Alternative specifications
On the basis of a number of issues raised in the above results it is useful to summarise briefly a number of alternative specifications to Model 2. Specifically, we consider the importance of the non-recursive structure and whether oil prices and money are needed in the model. We also consider including the foreign interest rate contemporaneously in the equations for the domestic variables in recognition of the fact that it is likely to reflect a range of external shocks other than just foreign monetary policy shocks.
First, if we estimate a recursive structural VAR model using the variables of the KR model, then we observe evidence of the price puzzle – a rise in the price level in response to a contractionary monetary policy innovation. It appears then that the non-recursive structure, that is the interdependence of the domestic monetary aggregate, interest rate and exchange rate, is an important structural feature of the model. This is consistent with arguments put forward by Kim and Roubini for the countries they consider as well as arguments presented in Cushman and Zha (1997). It is, however, a somewhat puzzling result since there is no obvious intuitive reason why this feature of the model resolves the price puzzle. This contrasts with the results for US studies where the role of a leading indicator of inflation can be readily explained (Sims 1992). This aspect of the model is somewhat troubling and merits further investigation.
As we discuss above, estimation results are broadly similar whether oil prices are included in the model or not; this variable does not perform any role as a predictor of inflation in terms of forward-looking monetary policy. The non-recursive structure and the other variables of the model, in particular the cash rate and exchange rate, appear to be sufficient. We also estimate a model where oil prices and money are both excluded. The model is identified in the same manner as Model 2. The results suggest that money is not playing an important role in the model either. The results are broadly consistent with Model 2 and they provide yet one more piece of evidence that one can abstract from movements in monetary aggregates when examining the effects of monetary policy. This is the strategy pursued by de Brouwer and O'Regan (1997) and by Dungey and Pagan (1998) and has the desirable feature of avoiding problems with instability in money demand.
Finally, previous discussions have emphasised the importance of including the Federal Funds rate in the domestic interest rate equation and, further, that external business cycle effects are reflected in movements of this variable. In this context, it seems sensible to include the contemporaneous foreign interest rate in the output and price equations as well. Doing so yields results similar to those from Model 2.
A simple means of summarising these alternative specifications is to provide the smallest dimensioned and least restrictive model that provides conclusions similar to Model 2:
For completeness, the estimate of B0 for this model is presented in Table 5. Inspection of this matrix indicates that it captures the same contemporaneous relationships between the variables as Model 2.
Footnotes
We also estimate a number of other variations. These are discussed in detail in Section 3.3.3 below. [15]
Related to this issue are comments by Gali (1998) on Bernanke and Mihov (1998). The latter presents a model in log levels as we do here. Gali argues that since estimation in levels tends to bias downward the parameter estimates on the first lag of the dependent variable such models may not provide very accurate representations of the data in small samples. This is particularly important for long-run effects since the bias is away from permanent effects. [16]
It is standard in the literature to consider innovations of one standard deviation in magnitude. Although it varies for each of the models we consider, the impact of a one standard deviation innovation to the interest rate always provides an impact effect on the domestic interest rate similar to 0.25 per cent. We focus on a 0.25 per cent impact effect on the interest rate because it is a magnitude relevant for policy analysis. [17]
Kilian's bootstrap procedure involves a preliminary bootstrap to correct possible bias in the coefficient estimates of the reduced form VAR. A subsequent bootstrap is used to calculate the empirical distribution of the impulse responses and the variance decompositions. We use 500 and 1,000 replications respectively. Following a suggestion in Kilian, the preliminary bias adjustment from the initial bootstrap is applied in the second bootstrap. In each of the second set of replications, the reduced form and the B0 matrix are estimated. [18]
A comparison of our impulse responses and confidence intervals with those of KR must be done with some care. First, KR uses a plus or minus one standard error band which is much narrower than the 90 per cent confidence interval we employ. Second, their bands are based upon Bayesian inference and have formally incorporated prior beliefs about the model. [19]
These standard errors are derived from the second derivative of the inverse of the Hessian matrix from the ML estimation. They are only approximate since we use a two step procedure. [20]
These results are not reported but are available from the authors upon request. [21]
VAR models with quarterly aggregate macroeconomic data are clearly not the best means of testing and examining an arbitrage hypothesis about financial markets. Our model does, however, encompass the endogenous monetary policy hypothesis put forward by McCallum (1994) to explain observed deviations from UIP. The results of the VAR analysis suggest that it might be a fruitful exercise to explicitly examine UIP and endogenous monetary policy. [22]
Although Dungey and Pagan restrict all direct contemporaneous effects of foreign variables to be zero in the interest rate equation, external business cycle effects are transmitted indirectly through domestic expenditure, output and inflation. [23]
See also the discussion in Faust (1998). [24]
One might query whether the fact that we can account for the forecast error variance of the nominal exchange rate in this manner suggests that we have a model that is able to forecast the exchange rate well. This is not, however, the case. All we have done is apportioned a large part of the model's forecast error variance to the variance of a particular structural innovation. We have not considered the absolute magnitude of the forecast error itself. Further, our results are based entirely upon within-sample analysis. A natural direction to pursue with the model we present is to consider explicitly its out-of-sample forecasting ability. So, for example, we could query whether our model outperforms a random walk forecast for the nominal exchange rate in out-of-sample experiments, similar to Meese and Rogoff (1993). Recent work by Robertson and Tallman (1999) suggests that examining the out-of-sample forecasting performance is an important concern for these types of models. We leave this for future work. [25]
Australia has only been a consistent net exporter of refined petroleum products since 1990, although it has been intermittently so since 1982 (ABARE (1998, pp. 298–305)). [26]
Using a random walk model for the interest rate is simply a modelling device used here for the simulations. It does not reflect a view that this is a sensible model of the policy interest rate variable. Sims and Zha use a slightly different approach, setting to zero all coefficients in the structural interest rate equation other than those associated with lags of the interest rate itself. Only for the policy shocks does this differ from the approach we use and, even then, by very little. For Bernanke, Gertler and Watson, where the focus is non-policy shocks, the approach is identical to that here. [27]
Gruen, Romalis and Chandra consider the effects of a one percentage point rise in the real interest rate. To compare with our results, we scale their results by ¼. [28]
These results are available from the authors on request. [29]
Most studies do take care to consider sample periods which are regarded as providing relatively stable and uniform monetary policy behaviour. Bernanke and Mihov (1995) is a good example. Nonetheless, the demands of VAR models make this difficult in many instances. [30]
Stevens (1999) cites a speech by the then Governor, Bernie Fraser, given in March 1993 (Fraser 1993) as the earliest statement of an explicit inflation target for the Reserve Bank. A number of other dates around this time could alternatively have been used. [31]
Since the procedure suggested by Chow assumes a constant variance across the two sub-samples in question, which is unnecessarily restrictive, we follow Mackinnon (1989) and use a heteroskedasticity-robust variant of Chow's alternative procedure (Davidson and Mackinnon 1993, pp. 399–402). [32]
For Australia, see de Brouwer, Ng and Subbaraman (1993). [33]