RDP 1999-04: Value at Risk: On the Stability and Forecasting of the Variance-Covariance Matrix 2. Stability of the Variance-covariance Matrix

The standard approach, when using the variance-covariance method of estimating VaR, is to use historical variances and covariances as the forecasts of the future variance-covariance matrix. This approach assumes that the variances and covariances are constant over the period of estimation and forecast.

We test this assumption using daily data for working days from 15 December 1983 to 29 October 1997. Nine foreign exchange rate returns and eight interest rate return series are used.^[1]

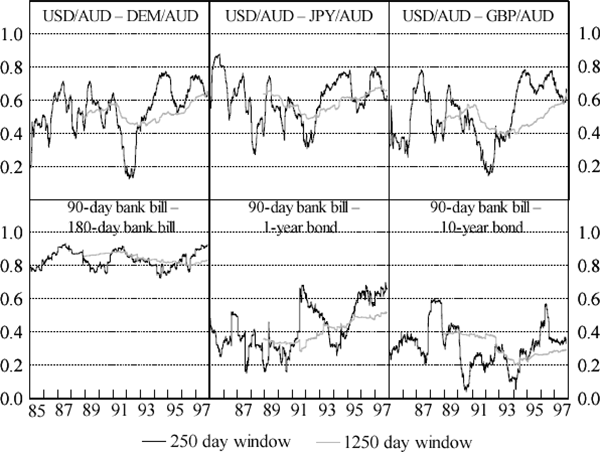
Figure 1 shows the correlation between selected pairs of exchange rate returns and interest rate changes. Correlations calculated using moving windows of 250 and 1,250 working days (that is, approximately one and five years) are shown. These graphs indicate, particularly when shorter window lengths are considered, that correlations move considerably through time.

To formally test this impression the global test for a constant unconditional correlation/covariance matrix as outlined in Jenrich (1970) is applied. This test quantifies the difference between two matrices via the trace of a relative difference matrix; the relative difference matrix being the difference between the two matrices divided by their sum.^[2] Firstly, within-asset class covariances and correlations are considered. The unconditional covariance and correlation matrices for the nine foreign exchange return series and the eight interest rate return series are analysed separately. The full sample was broken into separate fixed-length sub-periods. The Jenrich test is then applied to test the equality of each pair of matrices calculated from adjacent sub-periods. The analysis was repeated for sub-period lengths ranging between 125 and 1250 days.

The analysis was conducted for the full foreign exchange and interest rate covariance matrices and also for subsets of these matrices. The subsets considered were the Australian dollar against the US dollar, Japanese yen, German mark and British pound (major currencies); and the Australian dollar against the Canadian dollar, French franc, Dutch guilder and New Zealand dollar (other currencies) in the case of foreign exchange. For the interest rate series the subsets were the Treasury bond yields for one, two, five and ten-years (bond yields); and the yields on bank accepted bills of 30, 90 and 180-day maturities in conjunction with the overnight cash rate (discount securities). The numbers reported in Table 1 are the proportion of times a given covariance or correlation matrix was found to be equal to the matrix estimated from the following consecutive sub-period of data (at a 5 per cent level of significance).

It can be seen that the proportion of comparisons found to be equal is low. The results indicate that the correlation and covariance matrices are far from constant. In only one case was the correlation matrix stable over the full sample period. There is some tendency for correlations to be relatively more stable than covariances. To some extent this is to be expected since covariances reflect not just the relation between two series but the variances of the series as well. To the extent that variances are not stable this will be reflected in the covariances but not the correlations.

The statistical significance of the difference in the matrices appears to be an increasing function of the length of the sub-period compared. This could be indicative of a gradual change in the true covariance matrix over time. It can also be seen that instability is related to the dimension of the covariance matrix. Testing was carried out on various bivariate matrices to isolate any potential outlier within the full matrix. Appendix A reports the proportion of stable comparisons for the bivariate covariances and correlations. The USD/AUD and DEM/AUD covariance matrix and the 90-day bank accepted bill and overnight cash rate covariance matrix appear to be less stable than the other bivariate systems. However, removing these from the full analysis had no substantial effect. With the bivariate systems the proportion of stable matrices is dramatically increased. Thus it seems that the greater the number of financial-asset returns that a bank is exposed to the less stable will be the associated variance-covariance matrix.

Our results are consistent with Kaplanis (1988) in that the correlation matrix is relatively more stable than the covariance matrix. Kaplanis, however, found evidence of a constant correlation matrix over adjacent 46-month periods for ten stock markets' monthly returns over the period from 1967–1982. Longin and Solnik (1995) find the unconditional correlation matrix of monthly excess returns for seven countries' share price indices to be unstable over periods of five years. Sheedy (1997) applied the same test to equity index data for the US, UK, Japan, Germany and the World Index and foreign currency returns covering the US dollar against the British pound, Japanese yen, German mark; the British pound against the Japanese yen and German mark; and the Japanese yen against the German mark. Her results, with respect to the equity data, provide mixed evidence for the stability of the correlation matrix. She reports, however, that the foreign exchange data consistently reject the hypothesis of constant correlation. This is consistent with our findings.

When calculating the VaR measures it is common practice among banks to take full account of correlations within asset classes (for example, across a number of exchange rates or commodity prices) but to make more simplistic assumptions about correlations across asset classes (that is, between exchange rates, interest rates, equity returns and commodity returns). For example, the Basle Committee on Banking Supervision prohibited the use of empirical correlations when aggregating risk exposures across asset classes in their initial proposals to allow banks to use internally developed VaR models to determine required capital. One commonly cited rationale for this approach is that while reliance may be placed on within asset class correlations, correlations across asset classes are considerably more unstable.

To examine this proposition we examined the stability of a selection of correlations and covariances between exchange rates, interest rates and equity prices (the All Ordinaries Index). The results (shown in Table 2) are not significantly different from the within asset class bivariate analysis. Across-class correlations appear to be neither systematically more or less stable than correlations within asset classes (both in terms of the proportion of stable comparisons and the average magnitude of differences between matrices over time, as measured by the Jenrich statistic). This supports the Australian Prudential Regulation Authority's approach towards banks' internally-developed VaR models that may be used for capital-adequacy purposes which does not draw any distinction between across-class and within-class correlations.

Footnotes

The exchange rates are the Australian dollar against the US dollar, German mark, Canadian dollar, French franc, British pound, Japanese yen. New Zealand dollar, Swiss franc and Dutch guilder. The foreign exchange series are the indirect rates (that is, rates are expressed in terms of the foreign currency value of one Australian dollar). The interest rates are the overnight cash rate; the 30, 90 and 180-day bank accepted bill rates; and the 1, 2, 5 and 10-year Treasury bond yields. Returns are calculated as proportional changes in underlying rates. [1]

A variance-covariance matrix with dimension p has p(p−1)/2 + p independent elements, but the corresponding correlation matrix has only p(p−1)/2 independent elements since its diagonal elements are all unity. The Jenrich test has, in each case, an asymptotic chi-squared distribution with the number of degrees of freedom equal to the number of independent elements in the matrix. For testing the equality of the correlation matrix the test statistic has the form:

View MathML

where the Rs denote sample correlations, dg the diagonal operator, n₁ and n₂ the length of data used to estimate matrices R₁ and R₂ respectively and δ_ij the kronecker delta (one if i=j and zero otherwise). If the sample correlations are replaced by sample covariances, the first term in the equation above becomes the test for stability of covariances. The second term is hence, a correction employed when testing correlation matrices. [2]