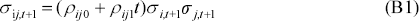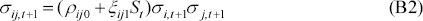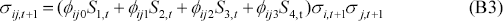Appendix B: Conditional Correlation Analysis | RDP 1999-04: Value at Risk: On the Stability and Forecasting of the Variance-Covariance Matrix

RDP 1999-04: Value at Risk: On the Stability and Forecasting of the Variance-Covariance Matrix Appendix B: Conditional Correlation Analysis

James Engel and Marianne Gizycki

May 1999

Download the Paper 604KB

Given the questions surrounding the constant correlation assumption various departures from the model are tested. Three alternative models are estimated along the lines of Longin and Solnik (1995). The constant correlation model is augmented with a time trend, threshold variables and asymmetry variables. The models are estimated over the full sample; over two halves of the sample; over four quarters of the full sample; and over consecutive 500 day periods. To simplify the analysis only bivariate systems involving the AUDYUSD paired with the eight other exchange rates and 90-day bank bill rate paired with the other interest rate series are used.

The covariance equation in the model augmented with a time trend (chosen arbitrarily as linear) has the form:

If the coefficient on the time trend is significantly different from zero then this provides evidence that the conditional correlation is not constant across time. Table B1 summarises the results from this exercise.

Table B1: Testing Constant Correlation GARCH Functional Form
Time trend
	Full sample	Half sample	Quarter sample	500 days
Foreign exchange	13.56^*	6.23^*	4.88^*	2.75^*
Interest rates	4.83^*	4.03^*	3.73^*	2.43^*
Threshold
Foreign exchange	6.28^*	4.74^*	3.14^*	2.14
Interest rates	4.31^*	5.02^*	3.47^*	2.03
Asymmetry
Foreign exchange (ϕ_ij₁ ≠ ϕ_ij₂)	2.48^*	1.58	1.83	1.43
Foreign exchange (ϕ_ij₀ ≠ ϕ_ij₃)	2.24	0.97	1.47	0.94
Interest rates (ϕ_ij₁ ≠ ϕ_ij₂)	2.38	1.99	1.53	1.39
Interest rates (ϕ_ij₀ ≠ ϕ_ij₃)	2.29	1.44	1.45	1.13
Notes: The results reported are the average standard t-statistic on the ρ_ij coefficient across time periods and all elements in the variance-covariance matrix. * denotes significance at the 5 per cent level.

The time trend coefficient is significant across all samples. Over the full period, therefore, covariances have significantly changed. It is worth noting that as the sample size decreases the time trend becomes less significant. To this extent smaller data windows, when no time trend is included, would be expected to give a more accurate representation of the evolution of the underlying process.

To test the hypothesis that correlations increase during periods of high volatility, a threshold effect is introduced into the bivariate system. With this threshold on correlation, the covariance term of the GARCH specification can be written as:

where S_t is a dummy variable that takes the value 1 if the estimated conditional variance of the USD/AUD exchange rate return is greater than its unconditional value and 0 otherwise. The threshold for the interest rate series is the variance of the change in the 90-day bank bill rate. This choice of threshold is arbitrary. The unconditional variance of innovations from the base model is taken as the exogenous threshold. The coefficient ξ_ij₁ will be positive if the correlation increases when the conditional variance is high. The average t-statistic on the dummy variable coefficient is shown in the table above.

The threshold coefficient is significantly different from zero in all cases except the 500 day window, hence, for the larger sized samples a threshold effect is present. This suggests that the use of shorter data windows may compensate for the failure to explicitly model a threshold effect. The threshold coefficients are significantly positive for all pairs of foreign exchange rates and longer-term interest rates indicating that periods of high volatility are associated with increased correlations.^[6] This is supportive of the stress-testing approach set out in APRA's market-risk reporting requirements which assumes that ‘worst case’ price movements occur simultaneously across a range of markets.

The third model looks at the issue of asymmetry. In the previous models a negative or positive shock is assumed to have the same impact on correlation. Here we test whether negative and positive shocks have a different impact on the conditional correlation. This augmented model conditions the correlation on both the sign and magnitude of past shocks to the USD/AUD exchange rate and for the interest rate matrix the 90-day bank bill rate. This asymmetric correlation GARCH has the following form:

where S_{k, t} are the dummy variables that take the values:

S₁, _t = 1 if ε_{i, t} is less than −σ_i and zero otherwise
S₂, _t = 1 if ε_{i, t} is less than 0 and zero otherwise
S₃, _t = 1 if ε_{i, t} is greater than 0 and zero otherwise
S₄, _t = 1 if ε_{i, t} is greater than σ_i and zero otherwise

Asymmetry is captured when ϕ_ij₁ ≠ ϕ_ij₂ and ϕ_ij₀ ≠ ϕ_ij₃. As can be seen from the results asymmetry does not appear to be present. This is consistent with the literature regarding foreign exchange series (Sheedy (1997)).

Footnote

The threshold coefficients are significantly negative for short-term interest rates. Hence, increased variation is associated with decreased correlation. This may reflect the interaction of the operation of monetary policy with market expectations. [6]