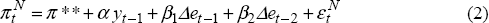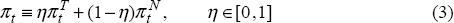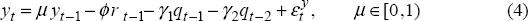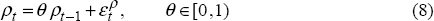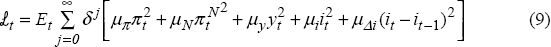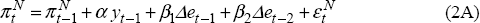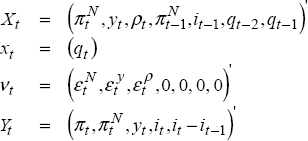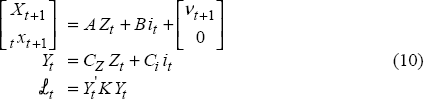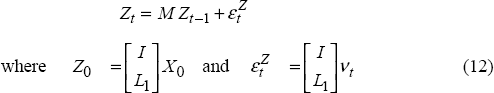RDP 9807: Inflation Targeting in a Small Open Economy 4. Theoretical Model

In this section of the paper we present a stylised model of a small open economy with a traded and non-traded sector. Our goal is to investigate the behaviour of key variables when targeting aggregate inflation as opposed to non-traded inflation.

4.1 The Model

We assume that traded and non-traded goods are produced and consumed in the domestic economy. The structure of the economy is described by five reduced form equations and three identities. An additional equation describes the central bank's objective function. The solution to the model is the path of the policy instrument, in this case the nominal interest rate, which minimises the objective function subject to the structure of the economy. (All variables are expressed as deviations from their long-run means and all coefficients are greater than, or equal to, zero.^[13])

Traded inflation

We assume that the country is small (that is, a price taker on world markets) and that there is no non-traded component in the final price of traded goods. For simplicity we assume that the world price of traded goods is constant and that pass-through is complete and instantaneous. Hence:

where π^T is the inflation rate of traded goods, e is the log of the nominal exchange rate (defined as the number of units of local currency per unit of foreign currency), and Δ is the first difference operator. In Section 6.2 of the paper we consider an extension to the model which allows for more gradual pass-through of the exchange rate.

Non-traded inflation (Phillips Curve)

The centre-piece of the model is an extension of the standard Phillips curve for non-traded inflation.^[14] Our reduced form specification is amenable to various assumptions regarding expectations and price formation:

where π^N is the inflation rate of non-traded goods and services, π^** is expected inflation (defined below), y is the output gap applicable to the non-traded sector, and ε^N is an independently and identically distributed (i.i.d.) shock to non-traded inflation, normally distributed with mean zero, and variance 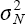. Hereafter we refer loosely to this as a supply shock, by which we mean any shock which causes a contemporaneous and unexpected change in non-traded inflation.

The term π^** represents a general form of inflation expectations. There are two avenues for consideration. First, expectations could be backward looking, forward looking, or some combination of both. This specification may directly capture the way in which agents form expectations.^[15] Alternatively, it may reflect the existence of overlapping contracts (Taylor 1980). Second, we examine two special cases, where π^** is the expectation of either non-traded inflation or aggregate inflation.^[16] Whereas firms care about the real product wage, workers care about the real consumption wage. More generally, there will be some bargaining between workers and firms, and π^** might be some combination of expected aggregate inflation and expected non-traded inflation.

Increases in the non-traded output gap cause higher non-traded inflation.

Finally, non-traded inflation may also depend on the cost of traded intermediate inputs. Firms in the non-traded sector are assumed to purchase traded intermediate inputs in advance of production. This effect is captured by the inclusion of lagged changes in the exchange rate.

Aggregate inflation identity

Aggregate consumer price inflation, π, depends on the long-run share of traded goods in consumption, η:^[17]

Non-traded output gap

The non-traded output gap is equal to (log) demand for the non-traded good, less (log) potential output of the non-traded good. For simplicity we assume that potential output in both sectors is fixed. Output in the short run is determined by the level of demand. Given that all series are demeaned, the non-traded output gap is equivalent to the demand for non-traded goods which depends on lags of both the real interest rate and the relative price of non-traded goods:

where r is the real interest rate, q is the relative price of non-traded to traded goods, and ε^y is an i.i.d. shock to demand for non-traded goods, normally distributed with mean zero, and variance 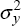. For ease of exposition we refer to this as a demand shock. The parameter μ captures the degree of persistence in demand.

This specification implies that it takes two periods for interest rate changes to have an effect on non-traded inflation via the demand channel. In addition, an increase in the relative price of non-traded goods is assumed to reduce demand in the non-traded sector, albeit with a lag. This mechanism drives the model towards long-run equilibrium in which the relative price of non-traded goods is unchanged.^[18]

The relevance of the non-traded output gap is justified by assuming that (at least in the medium term) factors of production are specific to each sector of the economy. Hence, only demand in the non-traded sector will have an impact on non-traded inflation. Alternatively we could develop a model where the focus is on aggregate demand. In this case there would be no role for the relative price of non-traded goods in determining aggregate demand. However, to close this model, we would need to include a role for the relative price of non-traded goods directly in the Phillips curve for non-traded inflation.^[19]

Nominal exchange rate

We assume Uncovered Interest Parity (UIP) which implies:

where i is the domestic nominal interest rate, i^f is the foreign interest rate (assumed to be zero for simplicity), ρ is a risk premium, and _tΔe_t+1 represents the expectation at t of the nominal depreciation between t and t+1.

Shocks to the exchange rate are an important focus of our paper. We model these shocks as changes in the risk premium which can exhibit persistence. This allows us to focus on shocks that are speculative in nature, rather than driven by fundamentals (such as the terms of trade).

Relative price identity

The relative price of the non-traded good is:

where p^N and p^T are the (log) price levels of non-traded and traded goods respectively.

Real interest rate identity

where π^* is the expectation of aggregate inflation (consistent with the form of expectations in π^**).

The risk premium

The risk premium is assumed to have some degree of persistence:

where ε^ρ is an i.i.d. shock to the risk premium, normally distributed with mean zero, and variance 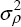. For expositional purposes we refer to this as an exchange rate shock.

The central bank's loss function

The central bank has a loss function which is generalised to incorporate preferences for targeting aggregate or non-traded inflation, as well as preferences for output stability and smoothing the path of interest rates:

where δ is the central bank's rate of time preference (0<δ≤1), and E_t (○) is the expectations operator taken at time t. The coefficients μ_π and μ_N reflect the central bank's preferences for aggregate or non-traded inflation being at target (the target is set to zero for simplicity). The coefficient μ_y represents a preference for maintaining output at potential.^[20] The coefficients μ_i and μ_Δi represent preferences for interest rate stabilisation, and interest-rate smoothing respectively.^[21]

4.2 Baseline Model Specification – Model A

The solution to the model is the path of the interest rate that minimises the loss function subject to the constraints implied by the structure of the economy. First we examine a very simple model with backward-looking inflation expectations and with π^** based on non-traded inflation. We refer to this as Model A:

Model A

Parameters

We choose parameter values that are broadly consistent with Australian data, and are comparable with those used by Haldane and Batini (1997), and Svensson (1998). Parameter values are presented in Table C1 in Appendix C. We present two sets of results, one where the central bank targets aggregate inflation, and one where the central bank targets non-traded inflation.^[22]

4.3 State-space Form and Solution

There is a standard technique for obtaining the solution to models with forward-looking variables. This technique requires that the equations be expressed in state-space form. Using the same notation as Svensson (1998), let X_t denote a vector of the predetermined variables and x_t denote a vector of the forward-looking variables. The vector of shocks to the predetermined variables is represented by v_t , and the vector of policy goal variables is denoted by Y_t. Finally, 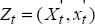is the combined vector of predetermined variables and forward-looking variables:

The vectors X_t, x_t, Z_t and Y_t are of length n₁, n₂, n = n₁ + n₂ and n₃ respectively (n₁ = 7, n₂ = 1 and n₃ = 5). The state-space form is as follows:

where A is an n × n matrix, B is an n × 1 vector, C_Z is an n₃ × n matrix, C_i is an n₃ × 1 vector, and K is an n₃ × n₃ diagonal matrix, with the preference weights on the diagonal (see Appendix B for more details).

This dynamic optimisation problem is solved in Backus and Driffill (1986), and applied in Svensson (1994, 1998). In models with forward-looking variables, the form of the solution depends on whether the central bank can pre-commit to an optimal policy rule. For now, we restrict our attention to the commitment solution and consider the alternative discretionary solution in Section 6.3. The commitment solution implies that the optimal interest rate will be a function of both predetermined variables and forward-looking variables, namely:

where N is an endogenously determined 1×n vector. The dynamics of the economy are as follows:

Matrices M and L₁ have dimensions n × n and n₂ × n₁ respectively; I is an n₁ × n₁ identity matrix, and X₀ is the initial value of the predetermined variables. A detailed description of the algorithm used to determine L₁, M and N is described in Backus and Driffill (1986) and Svensson (1994, 1998).^[23]

The solution to the model can be represented in a number of ways. We focus our attention on impulse response functions and the conditional variance of key variables. The impulse response functions describe the dynamic response of each variable to exchange rate, supply and demand shocks (equal to one standard deviation).^[24] We present the unconditional variance of each variable which describes the variability of the system when all shocks are operating. However, the unconditional variance depends on the assumptions regarding the relative size of each type of shock. Because of this, we prefer to focus on the variance of each variable conditional on the type of shock. In fact, the merits of aggregate versus non-traded inflation targeting depend critically on the type of shock under consideration. For a more detailed discussion of unconditional and conditional variances see Section 5.

Footnotes

The trend in the relative price of non-traded goods is easily removed if it is non-stochastic. A stochastic trend would be due to the effects of other variables not captured in our model. [13]

Although we discuss our specification of the non-traded Phillips curve, it is beyond the scope of this paper to derive it formally. [14]

It may be that price setting by firms follows a partial adjustment process as in Svensson (1998). For a discussion of how this can be incorporated into our model see Section 6.1. [15]

Taylor (1980) assumes that wages are the only source of nominal rigidity, while Calvo (1983) assumes that all nominal rigidities are in product markets. Svensson (1998) provides a structural aggregate supply equation for domestically produced goods based on nominal rigidities in product markets. We assume that when setting prices, non-traded firms have no regard for the relative price of non-traded to traded goods. However, this relative price does have a delayed impact through its effect on aggregate demand for non-traded goods. [16]

This share, η, is constant in the long run because the relative price of non-traded goods is assumed to be constant in the long run. [17]

We assume that the shocks have no long-run effect on the relative price of non-traded goods. [18]

Cursory evaluation of such a model suggested that it behaves similarly to the main model presented in this paper. [19]

The non-traded output gap is equivalent to the aggregate output gap in our model. The traded output gap is equal to zero because potential output is assumed fixed, and total demand (as opposed to domestic demand) for the traded good is constant. The latter point is implicit in our assumption of a constant price for traded goods in foreign currency terms. [20]

We present results based on μ_i = 0 and μ_Δi ≥ 0; the interest rate jumps in response to a shock, but by less than in the case where μ_i > 0 and μ_Δi = 0. [21]

Consistent with the observed practice of inflation-targeting, we assume that the central bank always places some weight on output stability and interest rate smoothing. [22]

The model was solved using Mathematica 3.0. Copies of the programs are available from the authors on request. [23]

The stylised nature of our model makes it difficult to interpret the exact length of one period. In our model the full effect of the real interest rate on demand occurs with a one-period lag. Gruen, Romalis and Chandra (1997) present evidence that for Australia, the effect of the interest rate on demand occurs over a lag of between 0 to 6 quarters. This suggests that in our model one period should be longer than one quarter, but perhaps shorter than one year. The length of a period also depends on assumptions regarding the persistence of output – higher persistence implies a shorter period length. [24]