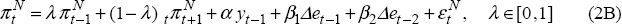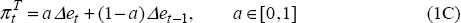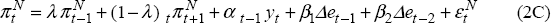RDP 9807: Inflation Targeting in a Small Open Economy 6. Extensions to the Basic Model

The main results from Section 5 are robust to alternative specifications. In what follows we adapt the model to include forward-looking inflation expectations, gradual exchange rate pass-through, and the case of discretionary policy.

6.1 Forward-looking Inflation Expectations

Consider a model in which expectations are forward looking in product markets. We refer to this as Model B:

Model B

The specification of Equation (2B) is consistent with a model of overlapping contracts (Taylor 1980). It is also consistent with partially forward-looking expectations in product markets.^[30]

As before, we focus on impulse response functions (Figure C1, Appendix C), and conditional variances (Table C2, Appendix C). The results for Model B are consistent with those of Model A. Namely, policy is more activist for exchange rate shocks when targeting aggregate inflation, and more activist under demand and supply shocks when targeting non-traded inflation.

Forward-looking inflation expectations appear to make the job of the central bank easier, as implied by the lower expected value of the central bank's loss function in Model B compared with Model A (Table C5). This is consistent with de Brouwer and Ellis (1998). However, in our model this result is contingent on the relative size of each of the three shocks. A comparison of conditional variances shows that the result is largely driven by the supply shock – the conditional variances in response to a supply shock are generally lower (than in Model A) under both regimes when inflation expectations are forward looking. In contrast, conditional variances for exchange rate and demand shocks are generally higher when inflation expectations are forward looking. This is primarily due to the behaviour of the real interest rate under forward-looking expectations.^[31]

6.2 Gradual Exchange Rate Pass-through

We extend Model B by incorporating gradual pass-through of the exchange rate into traded inflation. We assume that pass-through is complete within two periods. We refer to this as Model C:^[32]

Model C

The impulse response functions (Figure C2), and conditional variances (Table C3) for Model C yield the same broad results as Models A and B.

With gradual exchange rate pass-through, a positive supply shock increases inflation under both targeting regimes. The demand shock still reduces aggregate inflation initially, but to a lesser extent than in the case where pass-through is instantaneous. Even more gradual pass-through, perhaps even with a delay in pass-through, would be likely to reduce this initial fall in inflation in response to an inflationary demand shock. However, as we discussed in Section 5, this initial fall in aggregate inflation is in part caused by our assumption that the central bank observes and responds to the shock in the same period at it occurs; before the demand shock has led to a rise in non-traded inflation, and hence, in aggregate inflation.

Not surprisingly, the expected value of the central bank's loss function (Table C5) is considerably lower in Model C than either of the previous models, particularly in the case of aggregate inflation targeting.

6.3 Discretionary Solution

Thus far we have restricted our attention to the commitment solution. In models with forward-looking variables, there is generally a difference between commitment and discretionary solutions. In the case of commitment, the optimal interest rate today depends on the current value of forward-looking variables, which in turn depend on the expected future path of interest rates. However, under the discretionary solution the central bank can re-optimise every period and hence, cannot commit to the future path of interest rates.^[33] Because of this, the optimal interest rate at time t will depend only on the value of predetermined variables, and not on the value of forward-looking variables. That is:

where F is an endogenously determined 1 × n₁ vector. The forward-looking variables will also be a linear function of the predetermined state variables:

where C is an endogenously determined n₂ × n₁ matrix. The solution technique is described in Backus and Driffill (1986) and Svensson (1994, 1998).

Results for the discretionary solution to Model C are provided in Figure C3 and Table C4. Discretionary policy does not alter the main findings of the paper. Policy is more activist under aggregate inflation targeting for exchange rate shocks, and more activist under non-traded inflation targeting for supply and demand shocks.

Footnotes

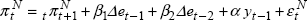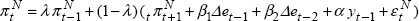With minor adjustments, Equation (2B) can be interpreted as capturing entirely forward-looking expectations, but with gradual adjustment (Svensson 1998). In the case of entirely forward-looking expectations and instant adjustment, the non-traded Phillips curve would be, . With gradual adjustment of prices, the relevant specification would be . [30]

For an inflationary exchange rate shock, the real interest rate rises by less than the nominal rate when expectations are backward looking. Hence, the nominal interest rate can be increased further to offset the rise in the risk premium, without producing as large a rise in real rates and, hence, output does not fall as far. In contrast, for an inflationary demand shock, the real interest rate rises by more when inflation expectations are backward looking; this is because the large appreciation actually reduces inflation initially. [31]

We altered the way in which the output gap enters the non-traded Phillips curve so that the aggregate demand channel can have an effect on inflation while the effect of exchange rate changes are still passing through to traded inflation. [32]

For a technical explanation of commitment versus discretion, see Oudiz and Sachs (1985) and Backus and Driffill (1986). [33]