RDP 9807: Inflation Targeting in a Small Open Economy 5. Results for Model A
July 1998
- Download the Paper 422KB
We consider two scenarios, one based on a flexible aggregate inflation target, and one based on a flexible non-traded inflation target (that is, μπ and μN are either 0 and 1, or 1 and 0 respectively, while μy = 0.5 and μΔi = 0.01).
The impulse response functions for Model A are shown in Figure 3.[25] First, consider the path of variables under aggregate inflation targeting, as indicated by bold lines. The left panel shows the response to a one standard deviation exchange rate shock (that is, a rise in the risk premium). The central bank raises interest rates to partially offset the depreciation implied by the shock. The nominal exchange rate depreciates initially and then gradually appreciates (that is, the exchange rate overshoots). Aggregate inflation moves in a similar fashion to the nominal depreciation due to the traded component, and because the response of non-traded inflation is relatively small. The real interest rate rise causes output to fall at the outset. As the real interest rate returns towards its neutral level, the stimulatory effect of the fall in the relative price of non-traded goods begins to dominate. This explains the rapid recovery in output. These factors combine to generate a cycle in output and non-traded inflation. The initial depreciation stimulates non-traded inflation through the influence of traded intermediate inputs. However, this is soon offset by the decline in demand, which leads to a fall in non-traded inflation, before the system returns to equilibrium.
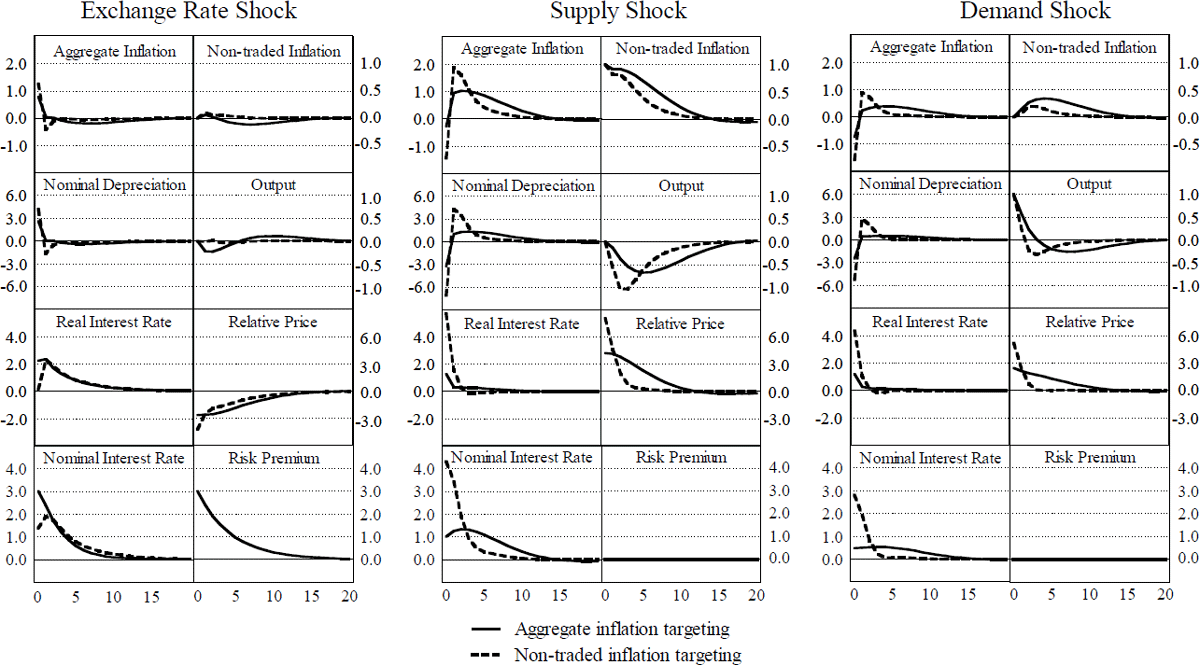
The impulse response functions for supply and demand shocks in Figure 3 are easily interpreted. In both cases the nominal interest rate rises, causing an initial exchange rate appreciation, followed by depreciation in subsequent periods. The real interest rate rises quickly and then falls away. The appreciation causes a jump up in the relative price of the non-traded good which acts in conjunction with the higher real interest rate to reduce output. Non-traded inflation moves in accordance with movements in output; the effect of changes in the cost of intermediate traded inputs is not particularly noticeable.
Turning to the case of non-traded inflation targeting, the relevant impulse response functions are represented by dashed lines in Figure 3. Compared with aggregate inflation targeting, the interest rate response is substantially smaller in the case of an exchange rate shock. The initial depreciation is greater, and aggregate inflation rises further. However, movements in the real interest rate and the relative price offset each other in terms of their effects on output which remains hardly changed. Non-traded inflation is less variable as expected.
In the case of supply and demand shocks the response of the interest rate is greater when targeting non-traded rather than aggregate inflation. This response is required to ensure a more rapid return of non-traded inflation and demand to equilibrium, but comes at the expense of a larger initial appreciation, and hence, a larger initial fall in aggregate inflation. The relative price rises further initially, but returns to equilibrium more rapidly.
One counter-intuitive result to emerge from Model A, is that aggregate inflation falls initially in response to inflationary supply and demand shocks. This result is in part due to our assumption of instantaneous exchange rate pass-through. The increase in interest rates in response to inflationary supply and demand shocks implies an exchange rate appreciation. This is fully reflected in aggregate inflation in the same period that the shock hits. In Section 6.2, we address this problem by considering a model with gradual exchange rate pass-through over two periods. In this specification, we demonstrate that an inflationary supply shock leads to an immediate increase in aggregate inflation (the appreciation feeds more gradually into traded inflation and aggregate inflation is dominated by the higher inflation of non-traded goods). Even so, gradual pass-through of this type is still not sufficient to ensure a rise in inflation initially following a demand shock.
The initial fall in inflation in response to inflationary demand shocks is also driven by another key assumption. Namely, we have assumed that the central bank observes and responds to shocks in the period they occur. In the period that an inflationary demand shock hits the economy, interest rates are increased and the exchange rate appreciates. This means that traded inflation falls instantly, whereas non-traded inflation rises in response to the demand shock with a one-period lag. This is why aggregate inflation falls initially with the shock. In reality there is likely to be a delay before the shock is observed and perhaps a further delay before policy responds, by which time the demand shock will have caused non-traded inflation to increase substantially. This would act to offset any fall in traded inflation (coming from an appreciation), and so aggregate inflation would always increase in response to an inflationary demand shock.
The variances of the key variables are shown in Table 2 for Model A under both targeting regimes. We examine two different measures of variance. The first, we call the unconditional variance. The unconditional variance of a series is calculated by assuming that all three shocks are active. This provides a realistic summary of the expected behaviour of the economy if the relative sizes of the shocks are accurate. The second measure of variance we call the conditional variance, which provides a measure of how the economy responds when only one of the three shocks is active.[26] This is a useful measure if there is little confidence in the relative size of the three shocks used when calculating the unconditional variances.
| π | πN | y | Δi | r | Δe | q | ||
|---|---|---|---|---|---|---|---|---|
| Shock | Aggregate inflation targeting | |||||||
| Unconditional | 2.96 | 2.52 | 2.28 | 3.45 | 4.63 | 6.16 | 12.08 | |
| Exchange rate | 0.93 | 0.29 | 0.47 | 3.22 | 4.20 | 2.80 | 6.34 | |
| Conditional | Supply | 2.50 | 2.35 | 1.77 | 1.12 | 1.47 | 4.66 | 9.03 |
| Demand | 1.28 | 0.85 | 1.35 | 0.50 | 1.29 | 2.89 | 4.90 | |
| Non-traded inflation targeting | ||||||||
| Unconditional | 3.97 | 1.89 | 2.31 | 5.99 | 8.33 | 12.09 | 12.70 | |
| Exchange rate | 1.34 | 0.14 | 0.07 | 1.60 | 3.68 | 4.57 | 6.04 | |
| Conditional | Supply | 3.16 | 1.85 | 1.99 | 4.79 | 5.96 | 9.25 | 9.55 |
| Demand | 1.99 | 0.35 | 1.16 | 3.21 | 4.51 | 6.29 | 5.80 | |
We begin with a comparison of the unconditional variances across both regimes. These show that targeting non-traded inflation causes an increase in the volatility of all variables (other than non-traded inflation), especially the interest rate and exchange rate. However, this result may be misleading because it could be altered by increasing the size of exchange rate shocks relative to supply and demand shocks. This is made clear by a comparison of the conditional variances across the two targeting regimes.[27]
Firstly, consider the case of supply and demand shocks. Given that the central bank has relatively little regard for volatility in the exchange rate when targeting non-traded inflation, it can move the interest rate further initially, and return the economy to equilibrium more rapidly. For these shocks, the variances of aggregate inflation, interest rates and the exchange rate are all higher under non-traded inflation targeting, while the variance of non-traded inflation is lower. The variance of output is lower under non-traded inflation targeting for a demand shock, but the opposite is true for a supply shock.
The interest rate response is greater for demand and supply shocks under non-traded inflation targeting compared with aggregate inflation targeting. The opposite is true for a shock to the exchange rate. A shock to the exchange rate has less effect on non-traded inflation and so there is less need to offset this shock with changes in the interest rate. Accordingly, when targeting non-traded inflation, the conditional variances of non-traded inflation, output, interest rates and the relative price are all lower for an exchange rate shock, while the variance of aggregate inflation and the exchange rate are higher.
In summary, neither aggregate inflation targeting nor non-traded inflation targeting produce consistently lower volatility in both product and financial markets across all types of shocks. This is true even though both regimes are flexible, with the same preference for output stability and interest rate smoothing. Policy under aggregate inflation targeting is more activist in the case of an exchange rate shock. This reduces the volatility of the exchange rate and aggregate inflation at the cost of greater volatility of the interest rate, output and non-traded inflation. In contrast, under non-traded inflation targeting policy is more activist in the case of supply and demand shocks. This reduces the volatility of non-traded inflation, at the cost of greater volatility in the interest rate, the exchange rate and aggregate inflation.[28]
These broad results are quite general and should hold for alternative model specifications and a range of parameter values, so long as three key assumptions are not violated. First, that the direct exchange rate channel has a more rapid effect on inflation than the aggregate demand channel. Second, that changes in the exchange rate have a greater impact on aggregate inflation over the short-term compared with non-traded inflation. Third that changes in the interest rate have a contemporaneous effect on the exchange rate. In the remainder of the paper we demonstrate that our main result is robust to alternative model specifications.
It is worth mentioning that we investigated a variant of Model A, where π** was based on aggregate inflation.[29] In this model, non-traded and aggregate inflation behave similarly. However, this result appears to be inconsistent with our empirical analysis, which demonstrated that non-traded and aggregate inflation move apart when there are significant changes to either the exchange rate or unit labour costs. Similar findings are likely in forward-looking models with π** based on aggregate inflation however, the solution to these models is not straightforward.
Footnotes
The optimal interest rate rule for Model A is described by the elements of the vector N in Equation (11). However, the interpretation of these coefficients is difficult because the contemporaneous relative price term is a forward-looking variable which responds to shocks instantaneously. In Section 6.3 we discuss discretionary policy in which the optimal interest rate is a function of only predetermined variables; this makes the rule easy to interpret. However, for consistency we did not report the results of optimal interest rate rules for any of the models in the paper (they are available from the authors on request). [25]
That is, the unconditional variance of the system assumes that σN = 1, σy = 1, and σρ= 3, whereas the variance conditional on say the demand shock assumes that σN = 0, σy = 1, and σρ= 0. [26]
Within a regime, unconditional variances are higher than each conditional variance because the shocks are uncorrelated. [27]
For supply and demand shocks the variance of output is roughly similar across both regimes, although the output gap closes more rapidly in the case of non-traded inflation targeting. [28]
This variant of the model behaves a lot like a version of Model A where the β parameters on exchange rate depreciation in Equation (2) are increased substantially. [29]