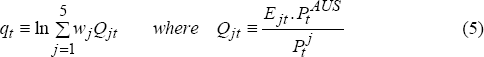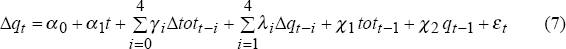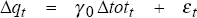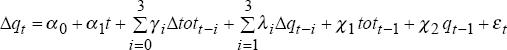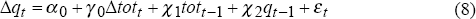RDP 9601: Why Does the Australian Dollar Move so Closely with the Terms of Trade? 3. Modelling the Real Exchange Rate

We construct a measure of Australia's real exchange rate as a trade-weighted arithmetic average of the real exchange rates of Australia's five largest trading partners, using trade weights derived from average annual trade flows over the two financial years 1984/85 and 1985/86.^[3] With out-of-sample forecasting beginning in 1987:Q1, this choice of trade weights again ensures that model-generated forecasts are truly ex ante. The measure of the real exchange rate, q_t, is therefore:

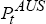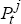w_j is the normalised country j trade weight, Q_jt is the Australia-country j real exchange rate, and are consumer price indices in Australia and country j, and E_jt is the price of the Australian dollar in country j's currency on the last day of quarter t.

Two time-series models for this trade-weighted real exchange rate, q_t, are estimated.^[4] The first, Model A, simply assumes that real exchange rate changes are determined by contemporaneous changes in Australia's terms of trade:

To derive the second time-series model for Australia's real exchange rate, we begin with an unrestricted error-correction model (ECM):

This specification allows for a longer-run relationship between the log-levels of the terms of trade and the real exchange rate. It also includes a time-trend to allow for the possibility that the real exchange rate and the terms of trade do not share the same longer-term trend. Since the relationship between the real exchange rate and the terms of trade may change over time, we generate preferred specifications over five sample periods, each with a starting date of 1984:Q1, but with end-dates extending in annual increments from 1989:Q4 to 1993:Q4.^[5]

For each sample period, we use a general-to-specific modelling approach. We test sequentially larger sets of exclusion restrictions on the regressors of the unrestricted ECM, leading eventually to identification of the statistically-significant regressors to be included in the estimated equation for the real exchange rate (see Appendix B for further details).

Three preferred regression specifications are identified. Thus, real exchange rate model B is given by:

for estimation periods ending 1986:Q4 to 1990:Q3,

for estimation periods ending 1990:Q4 to 1991:Q3,

for estimation periods ending 1991:Q4 to 1994:Q2.

Footnotes

Australia's five largest trading partners over the period, with normalised trade weights, were: Japan 0.4485, US 0.2896, UK 0.0969, W. Germany 0.0834, NZ 0.0816. [3]

We estimate the real exchange rate models over the post-float period; a sample so short that tests of non-stationarity generate ambiguous results. Tests on a longer sample of Australia's trade-weighted real exchange rate suggest it is stationary, possibly around a trend (Gruen and Shuetrim 1994). [4]

A preferred specification is assumed to remain the same for the three quarters following each end-date. Given the lack of degrees of freedom, we impose the model A specification given by equation (6) for sample periods ending before 1989:Q4. In these estimated equations, the coefficient on Δtot_t is always significant at the 5 per cent level. [5]