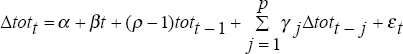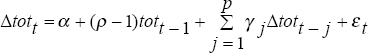RDP 9601: Why Does the Australian Dollar Move so Closely with the Terms of Trade? Appendix A: Stationarity Tests

The Augmented Dickey-Fuller (ADF) statistic, with constant and trend, is the value of the t-statistic for the estimated coefficient (ρ−1) from the regression:

Critical values for the null hypothesis, (ρ−1) = 0, in the presence of a constant and trend, at the 1 per cent, 5 per cent, and 10 per cent levels of significance are −4.15, −3.50 and −3.18 for sample size 50 and −4.04, −3.45, and −3.15 for sample size 100.

The ADF statistic, with constant and no trend, is the value of the t-statistic for the estimated coefficient (ρ−1) from the regression:

Critical values for the null hypothesis, (ρ−1) = 0, in the presence of a constant and no trend, at the 1 per cent, 5 per cent, and 10 per cent levels of significance, are −3.58, −2.93 and −2.60 for sample size 50 and −3.51, −2.89, and −2.58 for sample size 100.

The Dickey–Fuller Φ₃ test statistic, used to test the joint null hypothesis, β = 0 and (ρ−1) = 0, is defined by Φ₃ = (RSS_r – RSS_u).T / 2.RSS_u, where RSS_r is the residual sum of squares from the restricted regression when β = 0 and (ρ−1) = 0 are imposed jointly, RSS_u is the residual sum of squares from the unrestricted regression and T is the total number of observations in the sample. Critical values for the joint null hypothesis at the 1 per cent, 5 per cent, and 10 per cent levels of significance are 9.31, 6.73, 5.61 for sample size 50 and 8.73, 6.49, 5.47 for sample size 100.

The Ljung-Box Q statistic for M lags is given by Q(M) = T(T + 2)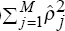/(T – j) where 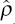_j is the sample autocorrelation of the residuals at lag j, j = 1,2,…, M. The null hypothesis under the Ljung-Box Q test is that the first M autocorrelations of the residuals are zero, and under this null, the statistic is distributed χ²_(M).

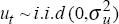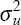Kwiatkowski, Phillips, Schmidt and Shin (1992) decompose the time series {y_t } into a linear trend t, a random walk r_t, and a stationary error term ε_t. Thus, y_t = ξ t + r_t + ε_t where r_t = r_t−1 + u_t and . The assumption of trend-stationarity in the series {y_t } implies the absence of the random walk component, or equivalently, that the variance of u, is zero. This is the null hypothesis in the KPSS unit-root test.