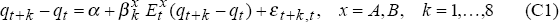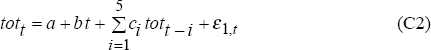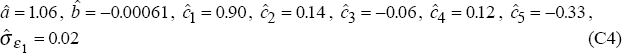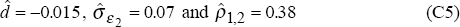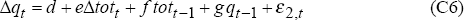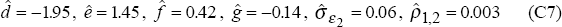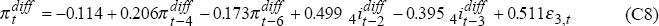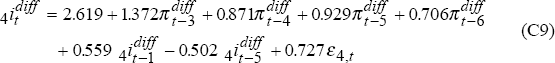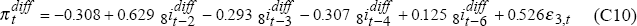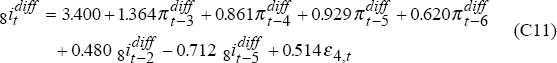RDP 9601: Why Does the Australian Dollar Move so Closely with the Terms of Trade? Appendix C: Monte Carlo Simulations
May 1996
- Download the Paper 204KB
This appendix outlines the Monte Carlo simulations used to generate results reported in Tables 5a, 5b and 6 in the text. Simulations are conducted assuming four different data generating processes (DGPs), which we examine in turn.
C.1 The Real Exchange Rate
To begin, we test the null hypotheses that our models of the real exchange rate have no
explanatory power, that is, that 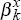 = 0 in each of the equations:
= 0 in each of the equations:
To test these null hypotheses, we assume a data generating process (DGP1) with the log terms of trade, tott, following the preferred specification identified in Section 2.2, and embodying the hypothesis that the real exchange rate is unforecastable:
Let 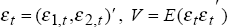 and
the estimates be
and
the estimates be 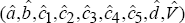 . Both equations are estimated by OLS, with
equation (C2) estimated over the full terms of trade sample, 1969:Q3 to 1994:Q2, and (C3)
estimated over the post-float period, 1984:Q1 to 1994:Q2. The off-diagonal elements of
V are derived from the correlation coefficient,
. Both equations are estimated by OLS, with
equation (C2) estimated over the full terms of trade sample, 1969:Q3 to 1994:Q2, and (C3)
estimated over the post-float period, 1984:Q1 to 1994:Q2. The off-diagonal elements of
V are derived from the correlation coefficient, 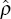 1,2,
of the estimated errors,
1,2,
of the estimated errors, 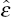 1,t and
1,t and 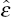 2,t
over the post-float period 1984:Q1 to 1994:Q2. The estimates are:
2,t
over the post-float period 1984:Q1 to 1994:Q2. The estimates are:
and
The Monte Carlo distributions are generated by running 5,000 trials with each trial (i = 1, …, 5,000) proceeding as follows.
-
Draw a vector sequence of observations
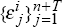 from a bivariate normal
distribution with mean 0, covariance matrix
from a bivariate normal
distribution with mean 0, covariance matrix 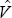 , n = 58
and T = 44. (n is the length of the pre-float terms of trade sample;
T is the post-float period, 1984:Q1 to 1994:Q4.)
, n = 58
and T = 44. (n is the length of the pre-float terms of trade sample;
T is the post-float period, 1984:Q1 to 1994:Q4.)
-
Generate sequences of observations
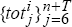 ,
, 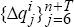 according to
according to 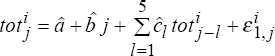 ,
,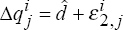
using (tot5,tot4,tot3,tot2,tot1) to start the autoregression. -
For time t,
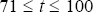 (t = 71 corresponds to 1987:Q1;
t = 100 to 1994:Q2) use the sequence of synthetic terms of trade data,
(t = 71 corresponds to 1987:Q1;
t = 100 to 1994:Q2) use the sequence of synthetic terms of trade data, 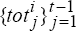 to
estimate the terms of trade model (C2) and thereby generate a vector of parameter estimates
to
estimate the terms of trade model (C2) and thereby generate a vector of parameter estimates
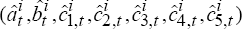 , and
hence derive
, and
hence derive 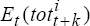 , k = 0,…, 8, t = 71,…,
100.
, k = 0,…, 8, t = 71,…,
100.
-
For time t,
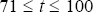 , use the sequences of synthetic data,
, use the sequences of synthetic data, 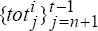 and
and
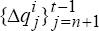 to
estimate a preferred real exchange rate model. For model A, this is equation (6) in the
text,
to
estimate a preferred real exchange rate model. For model A, this is equation (6) in the
text, 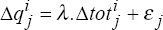 .
For model B, it is one of the three specifications in equation (8), depending on the time, t. Use this
preferred real exchange rate model, together with estimates of
.
For model B, it is one of the three specifications in equation (8), depending on the time, t. Use this
preferred real exchange rate model, together with estimates of 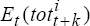 ,
derived above, to generate
,
derived above, to generate 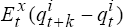 , x = A,B, k = 1,…, 8, t = 71,…, 100.
, x = A,B, k = 1,…, 8, t = 71,…, 100.
-
Estimate the regressions
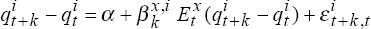 , t = 71,…,100,
by OLS for all values k = 1,…, 8, and for the two models and generate the
OLS t-statistics,
, t = 71,…,100,
by OLS for all values k = 1,…, 8, and for the two models and generate the
OLS t-statistics, 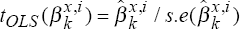 , x = A,
β.[10]
, x = A,
β.[10]
These 5,000 observations of tOLS 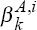 and tOLS
and tOLS
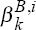 form the
Monte Carlo distributions under the null hypothesis that the models of the real exchange rate
have no explanatory power. Based on these Monte Carlo distributions, the results of the
hypothesis tests, H01:β = 0, for k = 1,…, 8,
are shown in column (x) in Table 5a for model A and in Table 5b for model B.
form the
Monte Carlo distributions under the null hypothesis that the models of the real exchange rate
have no explanatory power. Based on these Monte Carlo distributions, the results of the
hypothesis tests, H01:β = 0, for k = 1,…, 8,
are shown in column (x) in Table 5a for model A and in Table 5b for model B.
We turn now to the second data generating process (DGP2) which assumes that the real exchange rate model, estimated over the post-float period 1984:Q1 to 1994:Q2, is the true model. For this data-generating process, we again assume that the terms of trade follow model (C2) with parameter values (C4). The real exchange rate model (C3) is, however, replaced by:
with parameter values, estimated by OLS over the post-float period 1984:Q1 to 1994:Q2, given by:
The Monte Carlo distributions under this data generating process are again generated by running
5,000 trials with each trial (i = 1, …, 5,000) proceeding as before, but with
the following modifications. In step 2, the sequences of observations 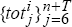 ,
,
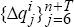 are now
derived from
are now
derived from 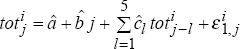 and
and 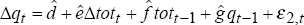 .
.
In step 5, after running the regressions 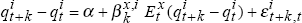 , x =
A,B, k = 1,…,8 we now collect the
coefficients,
, x =
A,B, k = 1,…,8 we now collect the
coefficients, 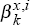 .
.
These 5,000 observations of 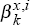 for the two models, x = A,B
and for each value of k form the Monte Carlo distributions under the assumption that
the real exchange rate is described by model (C6) with parameter values (C7). They are used to
test the null hypotheses, H02:β = 1, for k = 1,…,
8, with the results shown in column (xi) of Tables 5a and 5b.
for the two models, x = A,B
and for each value of k form the Monte Carlo distributions under the assumption that
the real exchange rate is described by model (C6) with parameter values (C7). They are used to
test the null hypotheses, H02:β = 1, for k = 1,…,
8, with the results shown in column (xi) of Tables 5a and 5b.
C.2 Excess Returns
The third data generating process, DGP3, combines the terms of trade and real
exchange rate models defined by equations (C2) and (C6) with parameter values (C4) and
(C7) – used for DGP2 – with models for the Australian-foreign
quarterly inflation differential, 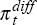 , and the one-year (four-quarter)
Australian-foreign nominal interest differential,
, and the one-year (four-quarter)
Australian-foreign nominal interest differential, 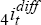 .
. 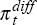 is defined
by
is defined
by 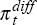 =
=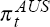 −
− 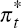 , where
, where 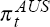 =
=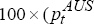 −
−
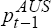 )
and
)
and 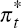 is
the trade-weighted foreign quarterly inflation rate,
is
the trade-weighted foreign quarterly inflation rate, 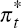 =
=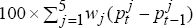 , and
, and 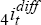 is defined
analogously.
is defined
analogously.
Simple bi-variate auto-regressive time-series models are fitted for 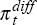 and
and 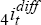 by
OLS using data from 1987:Q1 to 1994:Q4 and allowing up to six lags for each variable.
Eliminating insignificant lags leads to these models:
by
OLS using data from 1987:Q1 to 1994:Q4 and allowing up to six lags for each variable.
Eliminating insignificant lags leads to these models:
where ε3t and ε4t are uncorrelated i.i.d. N(0,1) random variables.
Assuming this data generating process, DGP3, Monte Carlo distributions are again
generated by running 5,000 trials with each trial i proceeding as for DGP2,
but with the following modifications. As well as generating sequences of observations 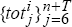 ,
, 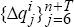 , we now
also generate sequences of observations
, we now
also generate sequences of observations 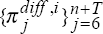 and
and 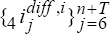 using (C8)
and (C9).
using (C8)
and (C9).
As for DGP2, for time t, 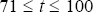 , we use the sequences
of synthetic data,
, we use the sequences
of synthetic data, 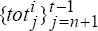 and
and 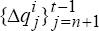 to estimate
real exchange rate model B (which involves estimating one of the three specifications in
equation (8), depending on the time, t). With this real exchange rate model, together
with estimates of Et(
to estimate
real exchange rate model B (which involves estimating one of the three specifications in
equation (8), depending on the time, t). With this real exchange rate model, together
with estimates of Et(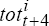 ), we generate
), we generate 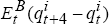 ,
t = 71,…, 100.
,
t = 71,…, 100.
At time t, the expected and actual excess returns to holding a one-year Australian
dollar bond rather than a trade-weighted basket of foreign bonds, are 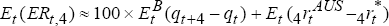 and
and 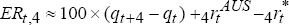 which
are equations (12) and (10) in the text. By construction, the expected real interest
differential using backward-looking inflationary expectations is
which
are equations (12) and (10) in the text. By construction, the expected real interest
differential using backward-looking inflationary expectations is 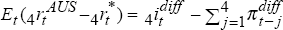 ,
while the actual real interest differential is
,
while the actual real interest differential is 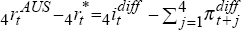 . Thus, for trial
i, the expected and actual excess returns are (approximately)
. Thus, for trial
i, the expected and actual excess returns are (approximately)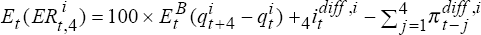 and
and 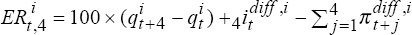 .
.
For trial i, we use the values of Et(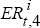 )
and
)
and 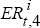 ,
, 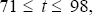 to run the
regression
to run the
regression 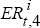 = αi + βi Et(
= αi + βi Et(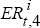 ) + εt.
The 5,000 values of βi form the Monte Carlo distribution with which the
hypotheses, H01:β = 0 and
H02:β = 1 are tested. The results are shown in the first row
of Table 6.
) + εt.
The 5,000 values of βi form the Monte Carlo distribution with which the
hypotheses, H01:β = 0 and
H02:β = 1 are tested. The results are shown in the first row
of Table 6.
The fourth data generating process, DGP4, combines the terms of trade and real
exchange rate models defined by equations (C2) and (C6) with parameter values (C4) and
(C7), with models for the Australian-foreign quarterly inflation differential, 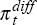 , and the
two-year (eight-quarter) Australian-foreign nominal interest differential,
, and the
two-year (eight-quarter) Australian-foreign nominal interest differential, 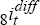 .
.
As before, simple bi-variate auto-regressive time-series models are fitted for 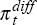 and
and 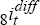 by OLS
using data from 1987:Q1 to 1994:Q4 and allowing up to six lags for each variable. Eliminating
insignificant lags leads to these models:
by OLS
using data from 1987:Q1 to 1994:Q4 and allowing up to six lags for each variable. Eliminating
insignificant lags leads to these models:
where, again, ε3t and ε4t are uncorrelated i.i.d. N(0,1) random variables.
The Monte Carlo distributions are derived as for DGP3, with the following
modifications. The expected and actual excess returns to holding a two-year Australian dollar
bond are 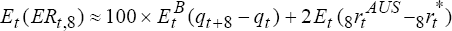 and
and 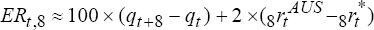 which
are equations (14) and (13) in the text. The expected real interest differential using
backward-looking inflationary expectations is
which
are equations (14) and (13) in the text. The expected real interest differential using
backward-looking inflationary expectations is 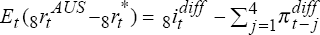 , while the actual
real interest differential is
, while the actual
real interest differential is 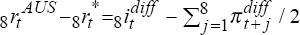 . Thus, for trial i, the
expected and actual excess returns are (approximately)
. Thus, for trial i, the
expected and actual excess returns are (approximately) 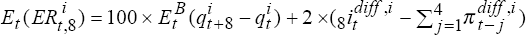 and
and 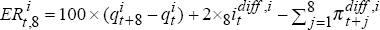 .
.
For trial i, we use the values of Et (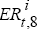 )
and
)
and 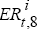 ,
, 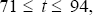 to run the
regression
to run the
regression 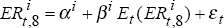 . Again, the 5,000 values of βi
form the Monte Carlo distribution with which the hypotheses,
H01:β = 0 and H02:β = 1 are
tested. The results are shown in the second row of Table 6.
. Again, the 5,000 values of βi
form the Monte Carlo distribution with which the hypotheses,
H01:β = 0 and H02:β = 1 are
tested. The results are shown in the second row of Table 6.
Footnote
As explained earlier, the actual exchange rate data ends in 1994:Q4, and hence the sample size is 30 for k = 1,2, but progressively less for forecasts further ahead (for k = 8, it is only 24). This pattern is replicated for the synthetic data. [10]