RDP 9502: Price Stickiness and Inflation 4. Testing the Ball-Mankiw Model With Industry Price Data
March 1995
- Download the Paper 136KB
We now turn to formal regression analysis of the industry price data to test the empirical implications of the Ball-Mankiw model. As mentioned in Appendix 2, microeconomic evidence on the frequency of price adjustments (Blinder, 1991; Cecchetti, 1986) suggests a period of six-months as appropriate for comparison with the model. We therefore present results using six-month price changes. We also present results with annual price changes to allow direct comparison with Ball and Mankiw's results for the US and to test the robustness of our conclusions.
In our regressions, the dependent variable is either the aggregate producer-price inflation rate or its change. In each case, explanatory variables are moments (standard deviation, skewness) of the economy-wide distribution of industry-price changes. Lags of the dependent variable are included in the regression to capture persistence.
Tables 2–5 compare annual results for the two twenty-year US sub-samples and for the Australian sample.[15] Over each roughly twenty-year sample, we assume that the average inflation rate is a good proxy for the average expected inflation rate. Then, the three samples with their different average inflation rates (1.3% p.a. in the US, 1949–69, 5.7% in the US, 1970–89, and 8.0% p.a. in Australia, 1972–92) allow us to test the model's predictions of the relationship between inflation and the moments of industry price changes as expected inflation changes.[16]
| Inflation Lagged 1 Year | Standard Deviation | Skewness | 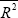 |
Spec. Test p-values | |
|---|---|---|---|---|---|
| United States | |||||
| 1949–69 Ave.Inf. = 1.3%pa |
−0.18 (0.21) |
−0.01 | 0.01 {0.48} |
||
| −0.14 (0.22) |
−0.24 (0.46) |
−0.05 | 0.011 {0.17} |
||
| 0.11 (0.23) |
−0.11 (0.42) |
0.007* (0.003) |
0.15 | 0.013 {0.80} |
|
| 1970–89 Ave.Inf. = 5.7%pa |
0.67** (0.17) |
0.42 | 0.04 {0.40} |
||
| 0.48* (0.20) |
0.53 (0.30) |
0.48 | 0.15 {0.30} |
||
| 0.39* (0.14) |
0.69** (0.22) |
0.014** (0.003) |
0.73 | 0.62 {0.89} |
|
| Australia | |||||
| 1972 – 92 Ave.Inf. = 8%pa |
0.83** (0.16) |
0.57 | 0.43 {0.48} |
||
| 0.73** (0.10) |
0.74** (0.14) |
0.82 | 0.77 {0.71} |
||
| 0.83** (0.09) |
0.70** (0.12) |
0.004** (0.001) |
0.88 | 0.001 {0.503} |
|
Notes: Data are annual. All regressions include a constant term (not
shown). OLS standard errors in brackets. *(**) implies that the coefficient estimate
is significantly different from zero at the 5%(1%) level. The specification test
p-values reported are for the Breusch Godfrey test for the presence of first to
second order serial correlation. p-values in {} are for the test of
heteroscedasticity, formulated as |
|||||
| Lagged Changes in Inflation | Standard Deviation | Skewness | 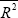 |
Spec.Tests p-values | |
|---|---|---|---|---|---|
| United States | |||||
| 1949–69 Ave.Inf.= 1.3%pa |
−0.77 [0.01] |
0.47 |
0.001 {0.00} |
||
| −0.90 [0.01] |
−0.91 (0.53) |
0.54 |
0.001 {0.002} |
||
| −0.89 [0.01] |
−0.32 (0.52) |
0.006* (0.002) |
0.66 |
0.003 {0.015} |
|
| 1970–89 Ave.Inf.= 5.7%pa |
−0.14 [0.08] |
0.22 |
0.33 {0.49} |
||
| −0.33 [0.08] |
0.19 (0.33) |
0.18 |
0.62 {0.46} |
||
| −1.04 [0.03] |
0.53 (0.29) |
0.014* (0.005) |
0.46 |
0.45 {0.93} |
|
| Australia | |||||
| 1972 – 92 Ave.Inf.= 8%pa |
−0.33 [0.51] |
−0.03 |
0.05 {0.79} |
||
| −0.74 [0.11] |
0.70** (0.22) |
0.37 |
0.39 {0.97} |
||
| −0.46 [0.05] |
0.71** (0.13) |
0.006** (0.001) |
0.78 |
0.17 {0.94} |
|
Notes: Data are annual. All regressions include a constant term (not shown). OLS standard errors in brackets. *(**) implies that the coefficient estimate is significantly different from zero at the 5%(1%) level. The specification test p-values reported are for the Breusch Godfrey test for the presence of first to second order serial correlation. p-values in {} are for the previously specified test for heteroscedasticity. Coefficients reported on the lagged changes in inflation are the sum of the coefficients on the first three lags. The corresponding test statistic, [ ], is the p-value on the test that the coefficients are all equal to zero. |
|||||
| Inflation Lagged 1 Year | Unemployment Rate | Standard Deviation | Skewness | 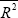 |
|
|---|---|---|---|---|---|
| United States | |||||
| 1949–69 Ave.Inf. = 1.3%pa |
−0.24 (0.22) |
−0.01 (0.006) |
−0.07 (0.44) |
0.08 |
|
| 0.008 (0.205) |
−0.011* (0.005) |
0.09 (0.38) |
0.007* (0.003) |
0.34 |
|
| 1970−89 Ave.Inf. = 5.7%pa |
0.73** (0.17) |
−0.019** (0.006) |
0.35 (0.24) |
0.67 |
|
| 0.57** (0.15) |
−0.012* (0.005) |
0.53* (0.20) |
0.011** (0.003) |
0.79 |
|
| Australia | |||||
| 1972 – 92 Ave.Inf. = 8%pa |
0.71** (0.11) |
0.003 (0.003) |
0.81** (0.15) |
0.82 |
|
| 0.81** (0.09) |
0.002 (0.003) |
0.74** (0.13) |
0.004** (0.001) |
0.88 |
|
Notes: Data are annual. The unemployment rate is adjusted by the Hodrick-Prescott filtered unemployment rate, regressions include a constant term (not shown). OLS standard errors in brackets. *(**) implies that the coefficient significantly different from zero at the 5%(1%) level. The specification test p-values reported are for the Breusch for the presence of first to second order serial correlation. p-values in {} are for the previously heteroscedasticity. |
|||||
| Lagged Change in Inflation | Unemployment Rate | Standard Deviation | Skewness | 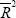 |
|
|---|---|---|---|---|---|
| United States | |||||
| 1949–69 Ave.Inf. = 1.3%pa |
−0.75 [0.03] |
−0.0046 [0.70] |
−0.89 (0.69) |
0.48 |
|
| −0.86 [0.03] |
−0.0034 [0.61] |
−0.15 (0.68) |
0.006* (0.003) |
0.63 |
|
| 1970–89 Ave.Inf. = 5.7%pa |
−0.58 [0.14] |
−0.027 [0.008] |
0.40 (0.25) |
0.61 |
|
| −0.99 [0.23] |
−0.023 [0.046] |
0.54 (0.25) |
0.008 (0.005) |
0.66 |
|
| Australia | |||||
| 1972 – 92 Ave.Inf. = 8%pa |
−0.65 [0.22] |
0.0043 [0.705] |
0.69* (0.24) |
0.29 |
|
| −0.47 [0.06] |
−0.0048 [0.57] |
0.74** (0.14) |
0.008** (0.002) |
0.76 |
|
Notes: Data are annual. The unemployment rate is adjusted by the Hodrick-Prescott filtered unemployment rate, include a constant term (not shown). OLS standard errors in brackets. *(**) implies that the coefficient estimate different from zero at the 5%(1%) level. Coefficients reported on the lagged changes in inflation are the sum of first three lags. The coefficient on unemployment is the sum of coefficients on the contemporaneous and corresponding test statistic, [ ], is the p-value on the test that the coefficients are all equal to zero. The specification reported are for the Breusch Godfrey test for the presence of first to second order serial correlation. p-values previously specified test for heteroscedasticity. |
|||||
The Tables report results using both inflation and its change as regressors. Tables 4 and 5 include (Hodrick-Prescott filtered) unemployment to capture the effect of the business cycle on inflation. The ‘change in inflation’ regressions (Tables 3 and 5) establish the robustness of the results and are also included because, in many cases, they eliminate serial correlation problems that are present in the ‘inflation’ regressions.
There are clear patterns in the regressions as the average rate of inflation rises. To begin, consider regressions including the standard deviation of industry price changes but not the skewness. At the lowest level of average inflation (1.3% p.a. in the US, 1949–69), the standard deviation of price changes is insignificant (and, in fact, slightly negative) in all the Tables. Moving down each Table, the average level of inflation rises and the estimated coefficient on the standard deviation of price changes also rises, becoming increasingly significant and, in most cases, adding progressively more explanatory power to the equations. As we have seen in Figure 5, the first model simulation predicts this rise in the coefficient on the standard deviation as expected inflation rises.
The skewness of industry price changes apparent from Table 1 and Figure 2 suggests that underlying shocks often have a skewed distribution. The logic of the Ball-Mankiw model then suggests that adding the skewness of price changes to the regressions should significantly improve their explanatory power.
The results are again very encouraging. Adding skewness to the regressions in Tables 2–5
always improves the regression 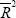 . The coefficient estimate on the
skewness variable is always positive, usually highly significant, and shows no obvious pattern
as average inflation changes. By contrast, there is a clear pattern in the estimated coefficient
on the standard deviation variable in these regressions. At the lowest average inflation rate,
this coefficient is of indeterminant sign and always insignificant. However, as average
inflation rises, the coefficient becomes highly significant and positive. These results are
strikingly similar to those from the model simulation that allows for a skewed distribution of
shocks (see Figure 7).[17]
. The coefficient estimate on the
skewness variable is always positive, usually highly significant, and shows no obvious pattern
as average inflation changes. By contrast, there is a clear pattern in the estimated coefficient
on the standard deviation variable in these regressions. At the lowest average inflation rate,
this coefficient is of indeterminant sign and always insignificant. However, as average
inflation rises, the coefficient becomes highly significant and positive. These results are
strikingly similar to those from the model simulation that allows for a skewed distribution of
shocks (see Figure 7).[17]
Table 6 shows Australian six-monthly results which are similar to the annual results. The coefficients on standard deviation and skewness are always positive as expected, with the former always highly significant.[18]
| Inflation Lagged 6 Months | Standard Deviation | Skewness | Unemploy. Rate | 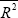 |
Spec. Test p-values |
|---|---|---|---|---|---|
| 0.82** (0.09) |
0.65 |
0.54 {0.15} |
|||
| 0.73** (0.08) |
0.35** (0.08) |
0.75 |
0.84 {0.74} |
||
| 0.75** (0.08) |
0.32** (0.09) |
0.0008 (0.0006) |
0.76 |
0.52 {0.86} |
|
| 0.74** (0.08) |
0.36** (0.09) |
0.0003 (0.0014) |
0.75 |
0.82 {0.74} |
|
| 0.75** (0.08) |
0.31** (0.09) |
0.0008 (0.0007) |
−0.0003 (0.0015) |
0.75 |
0.53 {0.86} |
Notes: Data are non overlapping, six monthly. The unemployment rate is the Hodrick-Prescott filtered unemployment rate, λ = 1600. All regressions include a constant term (not shown). OLS standard errors in brackets. *(**) implies that the coefficient estimate is significantly different from zero at the 5%(1%) level. The specification test p-values reported are for the Breusch Godfrey test for the presence of first to second order serial correlation. p-values in {} are for the previously specified test for heteroscedasticity. |
|||||
We now turn to an alternative regression specification to test the model prediction that the coefficient on the standard deviation of industry price changes is strongly dependent on expected inflation. The results in Figures 5 and 7 suggest that, at least for moderate rates of expected inflation, the product of expected inflation and the standard deviation of industry price changes (henceforth, the product variable) should provide a better explanation for inflation than the standard deviation on its own. Using the past year's inflation as a proxy for expected inflation, we use six-monthly data to examine this hypothesis in Table 7.
| Inflation Lagged 6 Months | Standard Deviation | St.Dev. x Past Annual Inflation | Skewness |
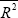 |
Spec. Test p-values |
|---|---|---|---|---|---|
| 0.73** (0.08) |
0.35** (0.08) |
0.75 |
0.84 {0.74} |
||
| 0.46** (0.11) |
4.34** (0.91) |
0.77 |
0.78 {0.71} |
||
| 0.75** (0.08) |
0.32** (0.08) |
0.0008 (0.0006) |
0.76 |
0.52 {0.86} |
|
| 0.50** (0.10) |
4.09** (0.87) |
0.0013* (0.0006) |
0.80 |
0.77 {0.90} |
|
| 0.40* (0.17) |
−0.16 (0.21) |
5.73* (2.28) |
0.0015* (0.0006) |
0.79 |
0.63 {0.86} |
Notes: Data are non overlapping, six monthly. All regressions include a constant term (not shown). OLS standard errors in brackets. *(**) implies that the coefficient estimate is significantly different from zero at the 5%(1%) level. The specification test p-values reported are for the Breusch Godfrey test for the presence of first to second order serial correlation. p-values in {} are for the previously specified test for heteroscedasticity. |
|||||
The results again support the model predictions. The product variable provides better explanatory power than the standard deviation variable, both with and without skewness in the regression. Furthermore, in the final regression in Table 7, the product variable dominates the standard deviation variable when both are included in the regression.[19]
Ball and Mankiw (1992b) argue that the inflation-skewness relationship is stronger than the inflation-dispersion relationship in the post WWII US. Our results suggest that the relative strength of these two relationships depends critically on expected inflation. For expected inflation below about 4 to 5 per cent per annum, the inflation-skewness relationship is relatively stronger. For higher expected inflation, however, the inflation-dispersion relationship is relatively stronger.[20]
The Ball-Mankiw observation that the skewness-inflation relationship is relatively stronger in the post-WWII US is then seen to be a consequence of the low average rate of expected inflation in the US over this time. By contrast, over our twenty year sample of Australian data, inflation (and, by inference, expected inflation) averaged 8 per cent per annum. At this rate of expected inflation, the dispersion-inflation relationship is almost twice as strong, empirically, as the skewness-inflation relationship.
To summarise, the empirical results support the detailed predictions of the Ball-Mankiw model. When average (expected) inflation is very low, a rise in the dispersion of shocks (and of price changes) has minimal impact on actual inflation while a rise in the skewness of shocks is inflationary. By contrast, when average (expected) inflation is higher, a rise in either the dispersion or skewness of shocks is inflationary.
4.1 Tests for exogeneity based on the terms of trade
As we have seen, the Ball-Mankiw model establishes a causal link from shocks to firms' optimal relative prices to their pricing behaviour and hence to aggregate inflation. There are, however, several plausible ways in which aggregate inflation or shocks to inflation may cause relative price variability rather than being a consequence of it (see, e.g., Sheshinski and Weiss, 1977 and Fischer, 1981). If so, there is an endogeneity bias in the regressions reported above because the regression error terms are correlated with at least one of the explanatory variables.
This sub-section examines this problem. It reports Hausman (1978) exogeneity tests for the standard deviation of industry price change variable in three of the Australian regressions already discussed. To conduct these tests, we need an instrument correlated with this variable but uncorrelated with the error term. Our choice of instrument is suggested by the nature of the Australian economy. Australia is small in world markets for almost all its traded-goods, implying that its terms of trade are exogenous to the Australian economy. Furthermore, as a commodity-exporting and manufactures-importing economy, Australia's terms of trade are among the most volatile in the OECD (Gruen and Shuetrim, 1994).
Since a terms of trade shock is a shock to the relative price of exports to imports and since both exports and imports form a substantial part of the Australian economy (with ratios to GDP of about 15% in the 1970s and early 1980s, rising to nearly 20% in the early 1990s) changes in the relative price of exports to imports should have a significant impact on relative prices in the wider economy.
Table 8 examines the impact of terms of trade changes on the standard deviation of industry price changes. The Table shows regressions both before and after the float of the Australian dollar and examines both six-monthly and annual industry price changes.[21] While terms of trade changes do not explain the standard deviation of industry price changes, the absolute value of terms of trade changes is a highly significant explanator of the standard deviation of industry price changes.[22] Thus, both favourable and adverse terms of trade shocks are associated with a high dispersion of industry price changes. By contrast, when the terms of trade are relatively stable, the dispersion of industry price changes across the economy tends to be low.
| Δ2TOT | AbsΔ2TOT | 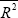 |
|
|---|---|---|---|
| Dependent Variable: Standard Deviation of Six Monthly Industry Price Changes (Δ2p) | |||
| Pre Float 1970:3 – 84:2 |
0.083 (0.083) |
0.023 |
|
| 0.23** (0.06) |
0.14 |
||
| Post Float 1984:3 – 92:4 |
−0.11 (0.08) |
0.048 |
|
| 0.28** (0.10) |
0.15 |
||
| Dependent Variable: Standard Deviation of Annual Price Changes (Δ4p) | |||
| Pre Float 1971:1 – 84:4 |
0.15 (0.11) |
0.12 |
|
| 0.37** (0.08) |
0.39 |
||
| Post Float 1985:1 – 92:4 |
−0.076 (0.055) |
0.074 |
|
| 0.19* (0.08) |
0.19 |
||
Notes: Data are quarterly. All regressions include a constant (not shown). ΔxTOT = ln(TOTt/TOTt-x), where x is two for six monthly price changes and four for annual price changes and AbsΔxTOT is the absolute value of ΔxTOT. Newey West standard errors, calculated using six lags, reported in brackets. *(**) implies that the coefficient estimate is significantly different from zero at the 5%(1%) level. |
|||
Given the earlier analysis in this paper, this result implies that both favourable and adverse terms of trade shocks are inflationary when expected inflation is high but not when it is low. In a future paper, we intend to examine these implications in more detail.
For the purpose of the current paper, however, the absolute change in the terms of trade is a natural instrument for the standard deviation of industry price changes. As well as being highly correlated with the standard deviation variable, this instrument should be uncorrelated with the regression error term.[23]
Table 9 reports IV and OLS regressions for three inflation regressions – chosen because they are representative and because the OLS regression errors show no signs of serial correlation. In each case, under the null hypothesis that the standard deviation of industry price changes is exogenous, the coefficient estimates from the IV and OLS regressions should not be significantly different.
| Dependent Variable: Change in Annual Inflation (annual data) | ||||||
|---|---|---|---|---|---|---|
| Lagged Changes in Inflation | Standard Deviation |
Skewness |
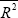 |
Hausman Test p-value |
||
| IVa | −0.30 [0.23] |
0.43 (0.41) |
0.006** (0.001) |
0.70 |
0.48 |
|
| OLS | −0.460 [0.046] |
0.71** (0.13) |
0.006** (0.001) |
0.78 |
||
| Dependent Variable: Six Monthly Inflation (six monthly data) | ||||||
| Inflation Lagged One Period | Standard Deviation | St.Dev.x ast Annual Inflation | Skewness | 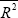 |
Hausman Test p-value |
|
| IVa | 0.79** (0.10) |
0.17 (0.23) |
0.0011 (0.0008) |
0.74 |
0.50 |
|
| OLS | 0.75** (0.08) |
0.32** (0.09) |
0.0008 (0.0006) |
0.76 |
||
| IVb | 0.40 (0.23) |
−0.38 (0.39) |
6.49 (3.37) |
0.002* (0.0008) |
0.77 |
0.74 |
| OLS | 0.40* (0.17) |
−0.16 (0.21) |
5.73* (2.28) |
0.0015* (0.0006) |
0.79 |
|
Notes: All regressions include a constant term (not shown). Standard
errors in brackets – *(**) implies that the coefficient estimate is
significantly different from zero at the 5%(1%) level. Coefficients reported on the
lagged changes in inflation are the sum of the coefficients on the first three lags.
The corresponding test statistic, [], is the p-value on the test that the
coefficients are all equal to zero. The final column reports the Hausman test
p-value for the null that the instrumented variable(s) is (are) exogenous. |
||||||
While the results are strongly suggestive that the standard deviation variable is exogenous, they are not decisive. The formal hypothesis that there is no difference between the coefficients is always easily accepted (see the p-values in the final column in the Table). However, in each case, instrumenting the standard deviation variable increases the estimated standard error considerably. As a consequence, although the coefficient on the standard deviation variable (or the product variable) in the IV regressions is always of the expected sign, it is not very significant.
Footnotes
The US data are the weighted results from Table II of Ball and Mankiw (1992b). [15]
These tests implicitly assume that the distribution of shocks in the two countries was similar – which is supported by a comparison of annual moments of industry price changes in the two economies (Table 1 and Ball and Mankiw, 1992b, Table II). [16]
Ball and Mankiw (1992b) do not point out that their model implies changing coefficients in these regressions as expected inflation changes. On the contrary, in their Table VII, they show regressions in which the estimated coefficients are relatively stable across the sub-periods 1949–69 and 1970–89. The relevant regressions in their Table include standard deviation, skewness and the product of standard deviation and skewness as regressors. Using our “double-normal-distribution” simulation and associated parameters, this regression does not have stable coefficients when expected inflation changes. The model coefficients on the relevant variables change by between a factor of two and four when expected inflation rises from its average rate in 1949–69 (1.3% p.a.) to its average rate in 1970–89 (5.7% p.a.) [17]
Note, however, that while the qualitative agreement between the model and the empirical results is impressive, the quantitative agreement is less so. We compare six-monthly results since the model parameters are chosen to match features of the six-month industry price moments. Including only standard deviation (SDP) in the regression, the first model simulation predicts a coefficient of 0.16 when expected inflation is 8% p.a., while the regressions in Table 6 give a coefficient estimate of about 0.35. Including both standard deviation and skewness (SKP ) in the regression, the second model simulation predicts coefficients of 0.019 and 0.0018 respectively when expected inflation is 8% p.a., while Table 6 gives coefficient estimates of about 0.3 and 0.0008. [18]
Figure 7 predicts a non-linear relationship between expected inflation and the coefficient on the standard deviation of industry price changes. To test this prediction, we included the product of standard deviation and the square of the past year's inflation in the final regression in Table 7. The coefficient on this variable was negative, as expected, but insignificant. [19]
This conclusion (and the one in the next paragraph of the text) is based on the penultimate regression in Table 7 and on the sample standard deviations of six-monthly moments of Australian industry price changes from Table 1. When past annual inflation is 4.5%, a one standard deviation shock to the standard deviation of industry price changes has the same predicted effect on inflation as a one standard deviation shock to the skewness of industry price changes. [20]
Since the sub-samples are short, we use overlapping data. For the six-monthly (annual) data, the post-float results start at 1984:3 (1985:1) to include only those price changes with a starting date after the December 1983 float of the Australian dollar. [21]
Chow tests suggest no evidence of a change in the coefficients between the pre and post-float regressions for either six-monthly or annual price changes (results not shown). [22]
The change in the terms of trade (rather than its absolute value) could be correlated with the error term in the regressions because it may affect inflation independently of its effect on the distribution of industry price changes. Possible channels for this link are the effect of a terms of trade change on domestic income and the nominal exchange rate, and via these, on inflation. However, since rises and falls in the terms of trade should have opposite effects on both income and the exchange rate, the absolute value of the change in the terms of trade should not be correlated with them and hence should not be endogenous to the regressions. As a further check, we repeated the analysis with regressions including H-P filtered unemployment (to control for excess domestic demand) and the change in the nominal trade-weighted exchange rate (TWI). Our conclusions are robust to these changes. [23]
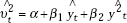 , where
vt are errors and yt the dependent variable.
The reported p-value is on the test that β1= β2= 0,
with the null of homoscedastic error variances.
, where
vt are errors and yt the dependent variable.
The reported p-value is on the test that β1= β2= 0,
with the null of homoscedastic error variances.