RDP 9502: Price Stickiness and Inflation 2. Australian Industry Price Data
March 1995
- Download the Paper 136KB
Our data are Australian Bureau of Statistics (ABS) quarterly producer prices for 95 Australian industries weighted by industry output from 1970:1 to 1992:4. With 95 industries, these data are at a quite disaggregated level: examples of the industries are “cement”, “footwear”, “paints” and “refrigerators”. The Data Appendix provides further details.
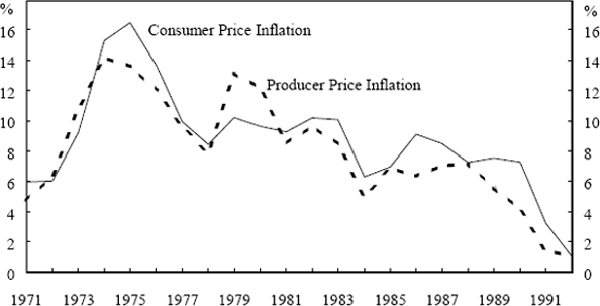
Figure 1 compares Australian annual industry price inflation (the weighted mean of log industry price changes) and consumer price inflation to show the close correspondence between the two series. Figure 2 shows the distribution of annual industry log price changes for four years in the sample (1972, '74, '85, and '92). In each year, the normal distribution with the same mean and variance as the distribution of industry price changes is also shown.[2] It is clear from the figures that price changes across industries show considerable dispersion. Over the sample, the annual industry price change averages 8% with a standard deviation (averaged across all industries and over time) of 5.5%.
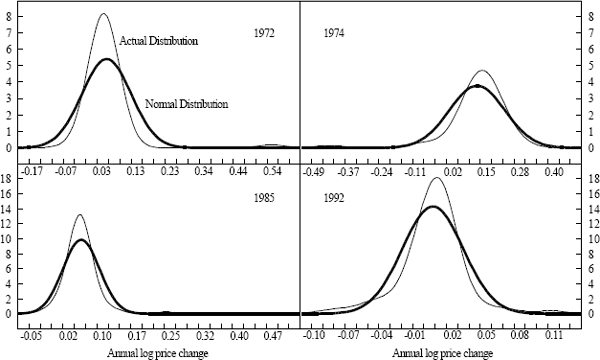
There is also considerable variation in the shape of the distribution of industry price changes. In 1972 and 1985, it is skewed to the right, in 1974 it is skewed to the left, while in 1992, the distribution is roughly symmetric.
Table 1 presents summary statistics for non-overlapping six-monthly and annual industry log price changes over the sample. In each case, the standard deviation and skewness of weighted log price changes across all the industries is presented along with the aggregate producer-price inflation rate (the weighted change in the log of the producer prices).
| Aggregate Producer Price Inflation | Standard Deviation of Industry Price Changes | Skewness of Industry Price Changes | |
|---|---|---|---|
| 1971 | 0.047 | 0.048 | −2.816 |
| 1972 | 0.063 | 0.074 | 5.918 |
| 1973 | 0.108 | 0.103 | 3.594 |
| 1974 | 0.142 | 0.106 | −3.194 |
| 1975 | 0.136 | 0.094 | −1.480 |
| 1976 | 0.120 | 0.048 | −1.638 |
| 1977 | 0.096 | 0.040 | −1.486 |
| 1978 | 0.078 | 0.040 | 0.911 |
| 1979 | 0.131 | 0.097 | 1.714 |
| 1980 | 0.121 | 0.052 | 1.885 |
| 1981 | 0.085 | 0.050 | −1.553 |
| 1982 | 0.096 | 0.053 | −0.333 |
| 1983 | 0.084 | 0.027 | 1.635 |
| 1984 | 0.050 | 0.027 | −1.292 |
| 1985 | 0.069 | 0.040 | 4.850 |
| 1986 | 0.064 | 0.066 | −1.278 |
| 1987 | 0.070 | 0.032 | 2.655 |
| 1988 | 0.072 | 0.054 | 1.597 |
| 1989 | 0.056 | 0.038 | −1.304 |
| 1990 | 0.041 | 0.054 | −1.716 |
| 1991 | 0.014 | 0.047 | −3.476 |
| 1992 | 0.010 | 0.028 | −0.008 |
| Mean | 0.080 | 0.055 | 0.145 |
| Standard Deviation | 0.037 | 0.025 | 2.567 |
| Correlation between Skewness and Standard Deviation | 0.053 | ||
| Dec-70 | 0.013 | 0.041 | −3.189 |
| Jun-71 | 0.025 | 0.026 | −2.197 |
| Dec-71 | 0.031 | 0.019 | −0.214 |
| Jun-72 | 0.029 | 0.038 | 5.395 |
| Dec-72 | 0.036 | 0.067 | 6.351 |
| Jun-73 | 0.051 | 0.073 | 5.107 |
| Dec-73 | 0.076 | 0.105 | 4.189 |
| Jun-74 | 0.062 | 0.057 | −2.956 |
| Dec-74 | 0.085 | 0.080 | −2.113 |
| Jun-75 | 0.065 | 0.049 | −1.317 |
| Dec-75 | 0.060 | 0.041 | 0.552 |
| Jun-76 | 0.065 | 0.023 | 0.329 |
| Dec-76 | 0.049 | 0.036 | −1.992 |
| Jun-77 | 0.054 | 0.030 | −0.996 |
| Dec-77 | 0.035 | 0.027 | −0.892 |
| Jun-78 | 0.035 | 0.027 | 1.500 |
| Dec-78 | 0.052 | 0.046 | 2.112 |
| Jun-79 | 0.066 | 0.069 | 1.984 |
| Dec-79 | 0.077 | 0.046 | 0.936 |
| Jun-80 | 0.062 | 0.035 | 2.009 |
| Dec-80 | 0.043 | 0.032 | −1.716 |
| Jun-81 | 0.044 | 0.028 | −1.225 |
| Dec-81 | 0.039 | 0.024 | −0.733 |
| Jun-82 | 0.047 | 0.038 | −1.652 |
| Dec-82 | 0.059 | 0.029 | 1.408 |
| Jun-83 | 0.041 | 0.020 | 1.728 |
| Dec-83 | 0.028 | 0.022 | 0.100 |
| Jun-84 | 0.023 | 0.021 | −1.755 |
| Dec-84 | 0.027 | 0.013 | 1.473 |
| Jun-85 | 0.034 | 0.023 | 1.296 |
| Dec-85 | 0.041 | 0.044 | 6.461 |
| Jun-86 | 0.024 | 0.045 | −2.312 |
| Dec-86 | 0.038 | 0.048 | −1.077 |
| Jun-87 | 0.033 | 0.029 | 1.035 |
| Dec-87 | 0.035 | 0.030 | 1.109 |
| Jun-88 | 0.038 | 0.037 | 3.534 |
| Dec-88 | 0.031 | 0.037 | 1.314 |
| Jun-89 | 0.027 | 0.026 | −0.374 |
| Dec-89 | 0.027 | 0.027 | −1.147 |
| Jun-90 | 0.017 | 0.030 | −3.255 |
| Dec-90 | 0.021 | 0.066 | −2.656 |
| Jun-91 | 0.001 | 0.034 | −2.027 |
| Dec-91 | 0.005 | 0.039 | 3.844 |
| Jun-92 | 0.002 | 0.023 | 2.575 |
| Dec-92 | 0.011 | 0.024 | −1.930 |
| Mean | 0.039 | 0.038 | 0.414 |
| Standard Deviation | 0.020 | 0.018 | 2.566 |
| Correlation between Standard Deviation and Skewness | 0.241 | ||
2.1 Are price falls special?
We can examine these industry-price data for evidence of any aversion by firms to price falls. To do so, we compare the proportion of industries in which the industry price fell with the proportion in which the price rose by more than twice the economy-wide producer price inflation rate (henceforth, the inflation rate).
Consider a simple model in which price-setting firms reset their output price every period. Assume that the ex ante distribution of shocks to firms' optimal price is symmetric.[3] Provided firms have no special aversion to price falls, the proportion of industries experiencing price falls should then be the same, on average, as the proportion experiencing price rises greater than twice the inflation rate. By contrast, if firms have an aversion to price falls, we should find a smaller proportion of price falls than price rises greater than twice the inflation rate.[4]
Figure 3 shows the proportion of industries with annual price falls and with annual price rises greater than twice the economy-wide inflation rate over the twenty-two years of the sample. There is no obvious evidence from the figure that price falls are less common than price rises greater than twice the inflation rate. Of the twenty-two years in the sample, the proportion of price falls is smaller than the proportion of price rises in eleven years – exactly half the time. There is no evidence here that firms display an aversion to price falls.
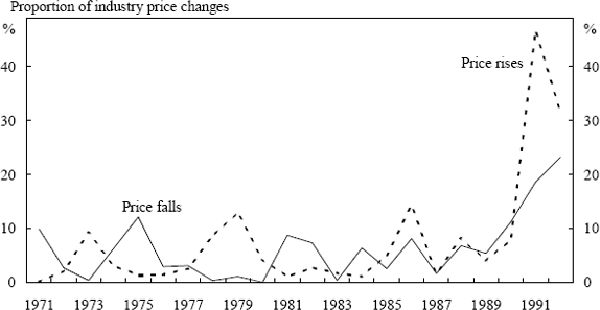
This analysis can be repeated using quarterly price changes rather than annual ones. Our sample of 91 quarterly price changes includes 4 quarters during which the average producer price fell. Excluding these quarters, in 46 of the remaining 87 quarters, the proportion of industries experiencing price falls was smaller than the proportion experiencing price rises greater than twice the quarterly inflation rate. 46 out of 87 is close enough to half to conclude that, at least at this level of disaggregation, there appears to be nothing special about price falls (see Appendix 1 for details of the appropriate statistical test).[5]
Footnotes
The distributions of industry price changes are estimated non-parametrically. For
industry i, define Δpi as the log price change and
ωi as the weight of the industry in the producer price index.
Then, the density function, f (Δp*) for log price
change Δp* is estimated as 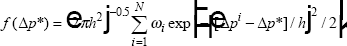 where
where
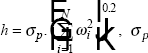 is
the weighted standard deviation of the industry price
changes Δpi , i = 1, …, N and N is the number
of industries in the sample (94 or 95). In all cases, the actual distribution of price
changes is more peaked than the normal distribution with the same variance.
[2]
is
the weighted standard deviation of the industry price
changes Δpi , i = 1, …, N and N is the number
of industries in the sample (94 or 95). In all cases, the actual distribution of price
changes is more peaked than the normal distribution with the same variance.
[2]
A symmetric ex ante distribution of shocks does not imply a symmetric ex post distribution of price changes across the economy in any given period. The data in Table 1 imply that the economy-wide distribution of price changes is often strongly skewed. Averaged over the whole twenty-year sample, however, the distribution of price changes is quite symmetric. [3]
Note that, with positive inflation, firms with an aversion to price falls can engineer a fall in their relative price by allowing their price to rise more slowly than the general inflation rate. [4]
Of course, the test does not distinguish between industries with differentiated and undifferentiated products, which may plausibly exhibit different behaviour. We will briefly return to the issue of firms' aversion to price falls in the next section. Lebow et. al. (1992) examine disaggregated data for both price and wage changes in the US and also conclude that there is little evidence of downward rigidity. [5]