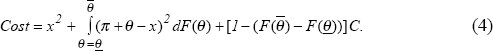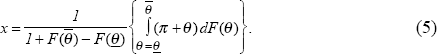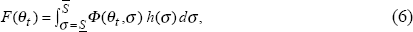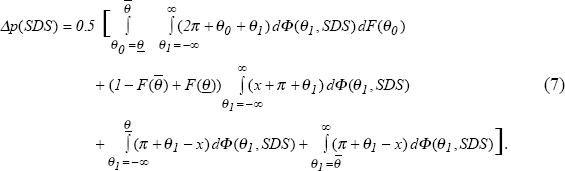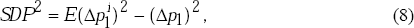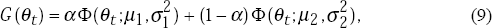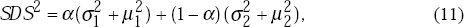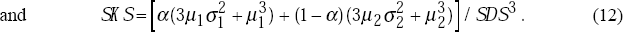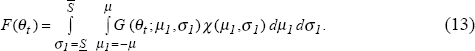RDP 9502: Price Stickiness and Inflation Appendix 2: The Ball-Mankiw Model

The model is set in discrete time in an economy consisting of a continuum of price-setting firms. Half the firms, “odd firms”, always adjust their output price in odd periods (t = 1,3,…) and half, “even firms”, always adjust in even periods (t = 0,2,…). The aggregate price level, p_t (all prices in logs) rises at an exogenously specified rate π and hence p_t = πt. All firms expect this rising aggregate price level.

Consider an even firm, and let x be the output price the firm sets in period 0. This price x will apply, at most, for periods 0 and 1 since the firm always resets its price in even periods. The model has three key assumptions.

Assumption 1: The firm can adjust its output price in period 1, but only by paying a menu cost, C.

Assumption 2: The firm's optimal relative price in period t,Θ_t, follows a random walk, Θ_t = Θ_t−1+θ_t, where θ_t are serially-uncorrelated mean-zero shocks with distribution function, F(θ_t).

Assumption 3: Any difference between the firm's actual price and its optimal price entails a cost equal to the square of this difference with the cost over two periods being the undiscounted sum of costs incurred in each period.

With the aggregate price level rising at rate π, the firm's optimal nominal price in period t is πt + Θ_t. As a normalisation, set Θ₀ = 0 , so the firm's optimal nominal price is zero in period 0, and π + Θ₁ ≡ π+θ in period 1 (dropping the subscript 1 when it causes no confusion). With a period 1 optimal price π+θ and an initial price x, the cost of not adjusting price in period 1 is (π+ θ − X)². Thus, the firm will not adjust in period 1 if (π+θ−X)²<C; that is if

Note a key implication of equation (3). With positive expected inflation, π, and provided X<π, the inaction band 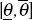is asymmetric. The firm adjusts its output price up in response to smaller positive shocks than it adjusts down in response to negative ones. Note also, that when 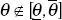, the firm pays the menu cost, C, and adjusts it's price to the period 1 optimal price, π + θ, simply because this price will only be in effect for this single period. In period 0, the firm minimises:

The first term is the firm's loss in period 0 when the optimal price is zero while the actual price is x. The second and third terms are the expected loss in period 1.

The loss is (π + θ − X)² when the firm does not adjust it's output price in period 1 while the loss is equal to the menu cost, C, when it does adjust. The first-order condition for minimising the cost with respect to x gives

Equation (5) has a simple interpretation. The price x is the weighted average of the firm's optimal price in period 0 and its expected optimal price in period 1 conditional on the initial price remaining in effect. The weights are the probabilities that x is in effect in the two periods, which are 1 for period 0 and 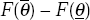for period 1. Together, equations (3) and (5) define x, 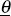and .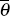

Inflation and the sectoral dispersion of shocks

We now derive the model relationship between inflation and the economy-wide dispersion of relative price shocks. By assumption, all firms in an industry have the same optimal price and, ex ante, all industries face the same distribution of possible shocks. We calculate the inflation rate between periods 0 and 1, and to do so, must specify the economy-wide distribution of shocks in several periods including period 1.^[24] For periods t≠1, we assume a general distribution of shocks, while the period 1 distribution is a particular realisation from this general distribution.

For periods t≠1, relative price shocks, θ_t, are drawn from a normal density N(0 ,σ ²) with the standard deviation, σ, drawn from a uniform density h(σ) with 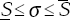. The distribution function for θ_t, t≠1 is then given by

where Φ(θ_t,σ) is the distribution function for the normal density N(0, σ²).

Period 1 industry-specific relative price shocks, θ₁, are distributed N(0,SDS² ) where σ = SDS (standard deviation of shocks) is a particular draw from the density h(σ). Period 1 has a large dispersion of shocks when 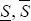or a small dispersion of shocks when .

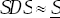All firms face the same menu cost, C, and so their price-setting can be derived from the analysis leading to equations (3) to (5).^[25] For given period 1 relative-price dispersion (given SDS ) the inflation rate between period 0 and period 1, Δp(SDS), is given by

The first term in this equation reflects odd firms that do not adjust their period −1 output price in period 0 while the second term reflects those that do. Even firms that adjust their period 0 output price down in period 1 are captured by the third term while those that adjust it up give the fourth term. Of course, firms which do not adjust their output price from period 0 to period 1 do not contribute to inflation between the two periods, Δp(SDS).

To derive the dispersion of industry price changes, SDP, we use the terms in equation (7) for the behaviour of the four groups of firms that change their output price in period 1, as well as for the aggregate price change. Then, defining the output price of firms in industry i in period t as 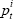and the aggregate price level as p_t, the standard deviation of industry price changes, SDP, is given by

where the expectation is over all industries i.

Following Ball and Mankiw, we assume that the menu cost for all firms, C, is C = (0.125)² which implies that firms tolerate a 12.5% deviation between their actual and optimal prices before making a special adjustment. We also assume prices are regularly adjusted once a year, so that the period of the model is six months. These assumptions are based on microeconomic evidence on the frequency of price adjustments (Blinder, 1991; Cecchetti, 1986).^[26]

Bounds on 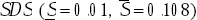are chosen to generate a standard deviation of the dispersion of industry price changes, SDP, that matches the Australian data.^[27] For given expected inflation, π, the model is used to generate actual inflation, Δp, and the inter-industry dispersion of price changes, SDP, as the inter-industry dispersion of shocks, SDS, varies uniformly over its range . Then the two OLS regressions in the text, equation (1), are estimated.

A Skew Distribution of Underlying Shocks

As before, we generate the inflation rate between periods 0 and 1 and the distribution of shocks for periods t≠1 is a general distribution while the period 1 distribution is a particular realisation from this general distribution. We begin with a distribution function

where Φ(θ_t;µ_i,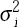), i=1,2 are normal distribution functions with means and variances as shown and α is the probability weight of the first normal distribution.^[28] Since G(θ_t) is a distribution of relative price shocks, θ_t must have mean zero, and hence

The standard deviation of the distribution of shocks, SDS, and the skewness of the distribution of shocks, SK S, are given by

We impose values for α and σ₂ to match moments of the distribution of Australian industry price changes (see later). With these imposed values and with equation (10) determining µ₂, the distribution function, G(θ_t), is a function of the moments of the first normal distribution, G(θ_t) ≡ G{θ_t;µ₁,σ₁). We assume µ₁ and σ₁ are independent and drawn from a uniform density χ(µ₁,σ₁) with −µ≤ µ₁≤µ and 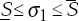. The chosen parameter values imply that when µ₁ <0 (and hence µ₂ > 0) the distribution is positively skewed, when µ₁ > 0 it is negatively skewed, while when µ₁ = 0, the distribution is symmetric. The distribution function for θ_t, t≠1 is then

Period 1 shocks, Θ₁, have a distribution function G(θ₁;m ,s) where μ₁ = m and σ₁ = s represent a particular draw from the density χ(µ_l,σ₁). Then, the dispersion and skewness of the distribution of period 1 shocks, SDS and SKS, are given by equations (11) and (12) with μ₁ = m and σ₁ = s. The distribution of θ₁ has a low (high) dispersion of inter-industry shocks when the derived value of SDS is small (large). Likewise, the derived value of SKS determines whether the distribution of period 1 shocks is symmetric, negatively skewed or positively skewed. Varying m and s independently in the parameter space defined by −μ ≤m ≤μ and 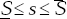, we determine how inflation varies with changes in SDS and SK S.

For given m and s, the inflation rate between period 0 and period 1, Δp(m ,s), is given by equation (7) with the new distribution function for period 1 shocks, G(θ₁;m ,s), replacing the earlier distribution function Φ (θ₁;SDS) and with F(θ) given by equation (13) rather than by equation (6) as it was previously.

Moments of industry price changes for the model are calculated as they were for the previous model. Using the new distribution functions, we use the terms in the inflation equation (equation (7)) for the aggregate price change and for the behaviour of the four groups of firms that change their output prices in period 1. Then, the dispersion (standard deviation) of industry price changes, SDP, is given by equation (8), while the skewness of industry price changes, SK P, is given by

where, as before, the expectation is over all industries i. Parameter values α = 0.975, −0.0167≤µ₁≤0.0167, 0.02≤σ₁≤0.05, σ₂=0.05 are chosen to match features of the Australian data and then the two OLS regressions in the text, equation (2), are estimated.^[29]

Footnotes

Odd-firm pricing behaviour in periods −1, 0 and 1, and even-firm pricing behaviour in periods 0 and 1 all contribute to the inflation rate between periods 0 and 1. [24]

The dispersion of period 1 relative-price shocks, SDS , is revealed in period 1. Thus, when even firms set their output price in period 0, they use the unconditional distribution function for θ₁, F(θ₁)where F(.) is given by equation ( Error! Bookmark not defined.). Of course, this is also the distribution function for next period shocks used by odd firms when they set their output price in period −1 or in period 1. Expected inflation for all firms is π , though, of course, actual inflation in period 1 will depend on the distribution of shocks. [25]

Blinder's survey of US firms with annual sales over $10 million reveals that 24.5% adjust prices more than twice a year, 20.3% adjust between once and twice and 55.1% adjust once or less than once a year. On average, these firms change their output price 3 to 4 months after a significant change in demand or cost conditions. [26]

Aggregate industry price inflation over our 1970–92 sample averages 8%p.a., while the dispersion across industries of (non-overlapping) six-monthly log price changes averages SDP = 0.038 and itself has a standard deviation (across different time periods) of 0.018. For the model, the standard deviation of the dispersion of price changes, SDP , is also 0.018 when π = 0.04 per period (8% p.a.) and SDS is distributed uniformly over the range 0.01= = 0.108. [27]

An alternative to this distribution is the skew-normal distribution analysed by Ball and Mankiw (1992b). However, the skew-normal distribution only permits a fairly narrow range of possible skewness (from −0.995 to 0.995) which seems too small to match the range of skewness in either the Australian or US industry-price data. When calibrated to match the Australian data, the distribution generated below has a standard deviation of the skewness of shocks equal to 3.6. [28]

As before, 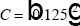is assumed. Recall that aggregate industry price inflation 1970–92 averages 8% p.a., while the dispersion across industries of (non-overlapping) six-monthly log price changes averages SDP = 0.038 over the sample and has a standard deviation (across time periods) of 0.018. Note further, that the skewness of the distribution across industries of these six-monthly log price changes averages SKP = 0.41 over the sample and has a standard deviation (across time periods) of 2.6. Imposing the parameter values in the text, when π = 0.04 per period (8% p.a.), and m and s vary uniformly over their allowed ranges, the standard deviations of both the dispersion of price changes, SDP , and the skewness of price changes, SKP , derived from the model match the Australian data values above. [29]