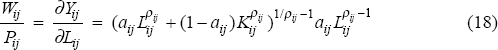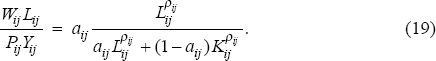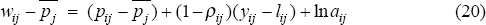RDP 9404: Wage Dispersion and Labour Market Institutions: A Cross Country Study 5. A Model of Wage Flexibility
June 1994
- Download the Paper 109KB
Our analysis in this section is based on a model with n countries each with m sectors containing a large number of identical firms. Output in each sector can be interpreted as being generated by a constant returns to scale, constant elasticity of substitution (CES) production function:
where i=1…m refers to a sector in country j=1…n, εij=1/(1−ρij) is the elasticity of substitution, and where the supplies of labour and capital in each sector are assumed to be fixed. As is well known, this production function encompasses the special case of ρij=0, implying εij=1, i.e. the Cobb-Douglas production function, with the labour share of output equal to aij, which is independent of the amount of labour and capital employed in production. A Cobb-Douglas production function may be a useful approximation for the economy in aggregate. Carmichael and Dews (1987) found this to be the case for Australia. For individual sectors, however, this may not be the case. The CES function may be a more appropriate choice using disaggregated data given its more generalised formulation.
Firms are assumed to maximise profits subject to the production function, leading to the first order condition that the real wage is equal to the marginal product of labour:
and thus the labour share of output in sector i, country j is given by
Taking logs and rearranging:
p¯ where variables in lower case are in logarithms, and where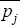 
is the price level in country j (e.g. the consumer price index).
Equation (20) is an equilibrium relationship between real wages, relative prices
and labour productivity which has an interesting implication for the conduct
of enterprise bargaining negotiations. It appears to be the case that, under
current enterprise bargaining arrangements, the sine qua non of any real wage increases is demonstrated productivity
improvements of equal size. Yet, from equation (20), it immediately follows
that the percentage change to the profit-maximising competitive wage in a particular
sector (or firm) is not in general equal to the percentage change in average
labour productivity. Only in the special case of Cobb-Douglas production (ρij=0)
and no relative price changes (i.e. pij − 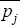constant over time)
will this be
so.[6]
More generally, even with unchanged relative prices, the warranted change in the real wage (in the sense of being consistent with a competitive market outcome) will exceed the change in productivity when the elasticity of substitution between labour and capital is small, with the converse true when this elasticity is large. Thus, a policy which seeks to impose real wage increases equal to increases in average labour productivity levels throughout the economy is not generally consistent with an efficient and competitive labour market, and may lead to distorted patterns of wages and employment, which is exactly the problem that enterprise bargaining is supposed to avoid.[7]
This policy issue aside, one way that we could uncover the degree of wage flexibility
in each country would be to regress the real wage wij − 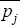on the relative price variable pij
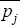− and the average level of labour productivity and test whether the coefficient on
the former is one and on the latter is 1−ρij.
However, this is impractical as we do not know the true value of the ρij's,
and cannot estimate them in the absence of reliable data on sectoral capital
stocks.
As an alternative, we construct sectoral wage, productivity and relative price variables for each country and conduct correlation and simple regression analysis to analyse the relationship among these variables. The variables are defined to be the relative deviations from their respective cross-sectoral means. The results from the correlation and regression analysis are compared across countries to determine which countries have the most responsive wage setting system.
In this model, the supplies of capital and labour are fixed in each sector. If we allow for factor mobility, the flexibility concept changes. In an economy with homogeneous workers and perfect labour mobility, workers would immediately move from one sector to another in response to wage differentials such that wage and productivity levels should, in effect, be equalised instantaneously across sectors. Wages would not appear to be responsive to productivity and prices, and the dispersion of wages across sectors would be zero. Alternatively, consider the case of some small degree of heterogeneous labour or costly mobility across sectors. Although wage and productivity deviations may be small compared to the fixed factor case, we would expect the relationship between wages and productivity to still be as strong if the market is sending the appropriate signals or is flexible. For example, in the case of a low (high) degree of mobility of labour, there would be a large (small) deviation of wages from mean and, correspondingly, one would expect the deviation of productivity from the mean to be large (small) as well. Provided factor mobility is not perfect, the relationship between wage and productivity deviations as measured by the correlation and regression coefficients should be unaffected by the degree of labour mobility. This follows from the fact that both coefficients are independent of scale.