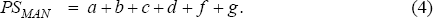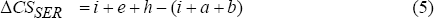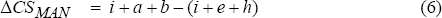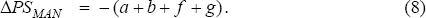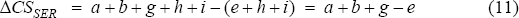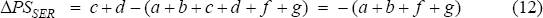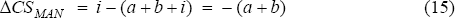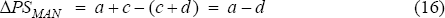RDP 9404: Wage Dispersion and Labour Market Institutions: A Cross Country Study 4. The Costs of Relative Wage Rigidity

Although the cost of relative wage rigidity has been asserted many times in the Australian literature, there has been surprisingly little attempt to demonstrate this cost theoretically (or empirically).^[4] In this section we present a simple diagrammatic analysis which illustrates the costs of relative wage rigidity. There are both welfare costs and losses in aggregate employment as well as a transfer of surplus from workers to firms.

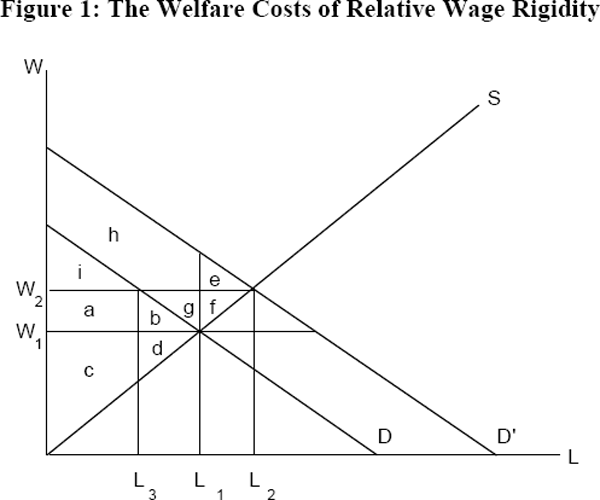
We assume that there are two sectors in the economy, services and manufacturing, with labour demand functions D and D′ respectively, as shown in Figure 1. The labour supply curve facing each industry is labelled S. Equilibrium in services is given by (L₁,W₁) and in manufacturing by (L₂,W₂). These sectors are segmented so that labour cannot flow from the low to the high wage sector. Consumer surplus (the surplus of firms who demand labour) and producer surplus (the surplus of workers supplying the labour) in the services sector are therefore given by:

and similarly for manufacturing:

Suppose that the services demand curve shifts out to D′ and the manufacturing demand curve shifts in to D with wages adjusting to restore equilibrium. Equilibrium in services is now given by (L₂,W₂) and in manufacturing by (L₁,W₁). By assumption, this equilibrium is established by labour supply responses within the two segmented labour markets, rather than between them. The change in consumer surplus in each sector is given by:

while the changes in producer surplus are given by:

The net change in consumer surplus accruing in services is in two parts: the gain on the marginal units of labour e, the gain on the inframarginal units h and the loss on the inframarginal units a+b. Whether this net change is positive or negative depends on the slopes of the curves and the size of the shift in the demand curve.

The net gain in producer surplus in services can also be broken into two parts: the gain to the inframarginal units a+b+g and the gain to the newly employed marginal units f. This net gain is unambiguously positive.

The overall gain (sum of ΔCS and ΔPS) in services is also unambiguously positive, and is given by the area e+f+g+h. Additionally, there is a redistribution of welfare from firms to workers of a+b.

The gains and losses in the manufacturing sector are the mirror image of those in services, so that the net welfare gain to the economy is zero. There is however a transfer of welfare from the contracting sector (manufacturing) to the expanding sector (services) of e+f+g+h.

Suppose now that, in the face of these demand shifts, the wage in each sector does not change i.e. the wage is fixed at W₁ in services and at W₂ in manufacturing. Assume that labour employed is the minimum of demand and supply at the prevailing wage (the usual assumption in disequilibrium models).

The wage and employment levels in services are given by (W₁,L₁), i.e. the pre-demand shift equilibrium, with

Relative to the post-demand shift, flexible wage equilibrium analysed above:

The effects of the rigidity on the welfare of firms in services is ambiguous. On the one hand, they gain a+b+g by not having to pay a higher wage to the inframarginal labour units. On the other hand, they lose the surplus on the marginal units they would have gained had the wage been allowed to rise, and these units been employed. This amount is given by the area e.

The effects of this rigidity on the welfare of workers in services is unambiguously negative. The inframarginal units lose a+b+g, the extra wage payments they would have received if the wage had been allowed to rise, while the marginal units of labour which are now not employed lose an amount given by f.

Welfare in the services sector as a whole is down by an amount equal to e+f, and there is a transfer from workers to firms equal to a+b+g. Employees are worse off compared to the flexible wage equilibrium because there are fewer of them (L₁ rather than L₂), and they are paid less (W₁ rather than W₂).

In the manufacturing sector the wage and employment levels are given by (W₂, L₃), with

Relative to the flexible wage equilibrium analysed above:

The firms lose an amount a from having to pay their inframarginal units more than if the wage were allowed to fall, and an amount b, the surplus from the marginal units they would employ in a flexible labour market, but now do not. Employees gain the amount a (the inframarginal workers do not now take a pay cut), but lose the amount d, the surplus to the workers who would be employed if the wage were allowed to fall.

Welfare in the manufacturing sector as a whole is down by b+d, and there is a transfer from firms to workers equal to a.

For the whole economy the rigidity of each wage leads to:^[5]

• an efficiency loss of (b+d+e+f);
• a loss of employment of (L₂−L₃); and
• a transfer of (b+g) from employees to firms.

Footnotes

Keating (1983) addressed this issue using Australian data over the period 1948/49 through 1979/80. Using a simple supply and demand model he concluded that notwithstanding Australia's highly centralised system of wage determination, wages have been permitted to move “in generally the right direction” over the period. [4]

We have no way of knowing whether these static losses are large in practice. It is possible that, were they to be estimated, the amounts would be surprisingly small, just as the static welfare losses from restrictions on international trade are also usually estimated to be small (Deardorff and Stern, 1986). However, if these distortions have dynamic effects i.e. affect the growth rate of national income and not just its level, then the cost of relative wage rigidity will probably be quite large, as has recently been found for the dynamic effects of trade restrictions. [5]